g-xTB - A General-Purpose Tight-Binding Electronic-Structure Method

Legend of Saint Francis fresco, potentially by Giotto
GFN2-xTB has for years occupied an odd niche in computational chemistry. It is not a density functional, nor a force field, nor quite a machine-learned potential. It is a parameterized tight-binding method that produces molecular geometries and noncovalent interactions fast enough for large-scale conformer searches, implicit solvent calculations, or molecular dynamics runs where DFT would be prohibitive. It is also—depending on your application—either "good enough" or "dangerously misleading."
GFN2-xTB and other low-cost methods have well-known limitations: reaction barriers come out too low, orbital gaps are compressed, and transition-metal complexes can sometimes distort into unphysical geometries. The method's speed and black-box nature keep it in use, but GFN2-xTB is a poor surrogate for DFT in many areas.
The new g-xTB method from Grimme's group (preprint) is explicitly intended as a general replacement for the GFN-xTB family. The "g" stands for "general," and the idea is not just to tweak parameters but to address three structural problems in GFN-xTB:
- No Hartree–Fock exchange. GFN2-xTB emulates a GGA functional, which is fine for geometries but systematically weak for thermochemistry and barrier heights.
- Minimal basis sets. The traditional STO-nG-like bases don't adapt to molecular environments and lack polarization functions on key elements.
- Narrow training scope. Parameterization focused on a few property types, not on broad coverage of chemical space.
g-xTB keeps the tight-binding framework but changes a lot of the underlying machinery:
- A charge-dependent, polarization-capable basis ("q-vSZP") that adapts AO shapes to local charge and coordination.
- An extended Hamiltonian with range-separated approximate Fock exchange for more realistic barriers and orbital gaps.
- Higher-order charge terms in the density-fluctuation expansion, including an explicit first-order term that fixes pathological small-cation cases.
- Atomic correction potentials (ECP-like projectors) to compensate for basis set incompleteness.
- A charge-dependent repulsion term to reduce overstabilization of strained geometries.
Performance
On the GMTKN55 database (~32,000 relative energies covering thermochemistry, kinetics, and noncovalent interactions), g-xTB's WTMAD-2 is 9.3 kcal/mol, roughly half that of GFN2-xTB and in the same range as some "cheap" DFT methods. This is a big step forward, and establishes g-xTB as a valid drop-in replacement for low-cost DFT methods in a variety of settings:
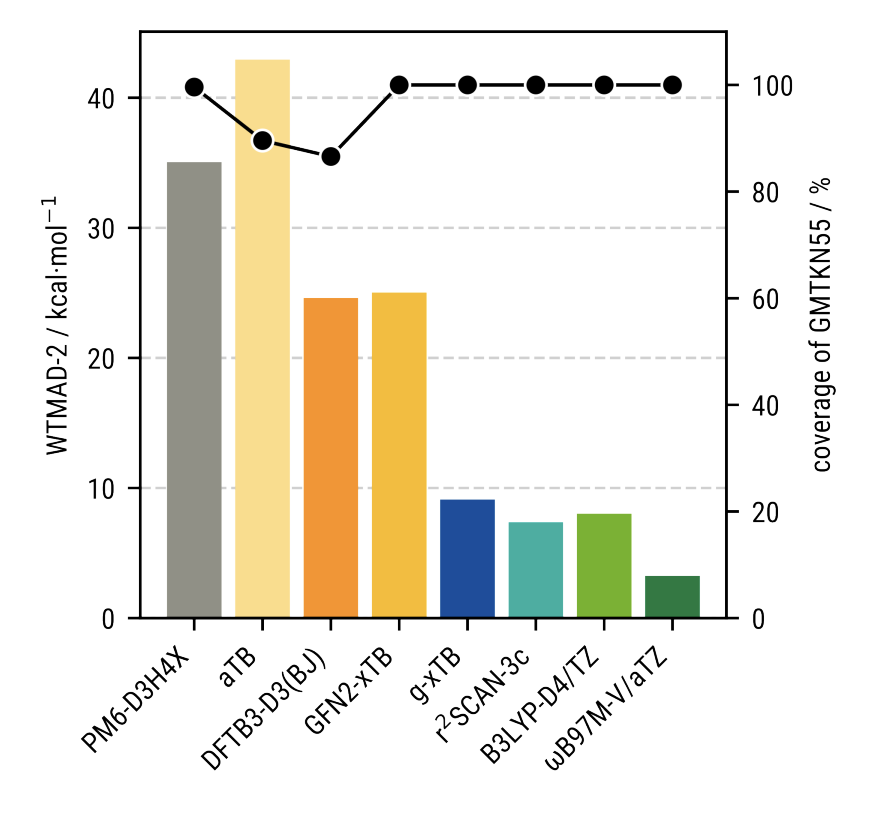
The performance of g-xTB on the GMTKN55 benchmark set.
There are also improvements to specific problem areas. Reaction barriers are much accurate owing to the presence of approximate range-separated Fock exchange:
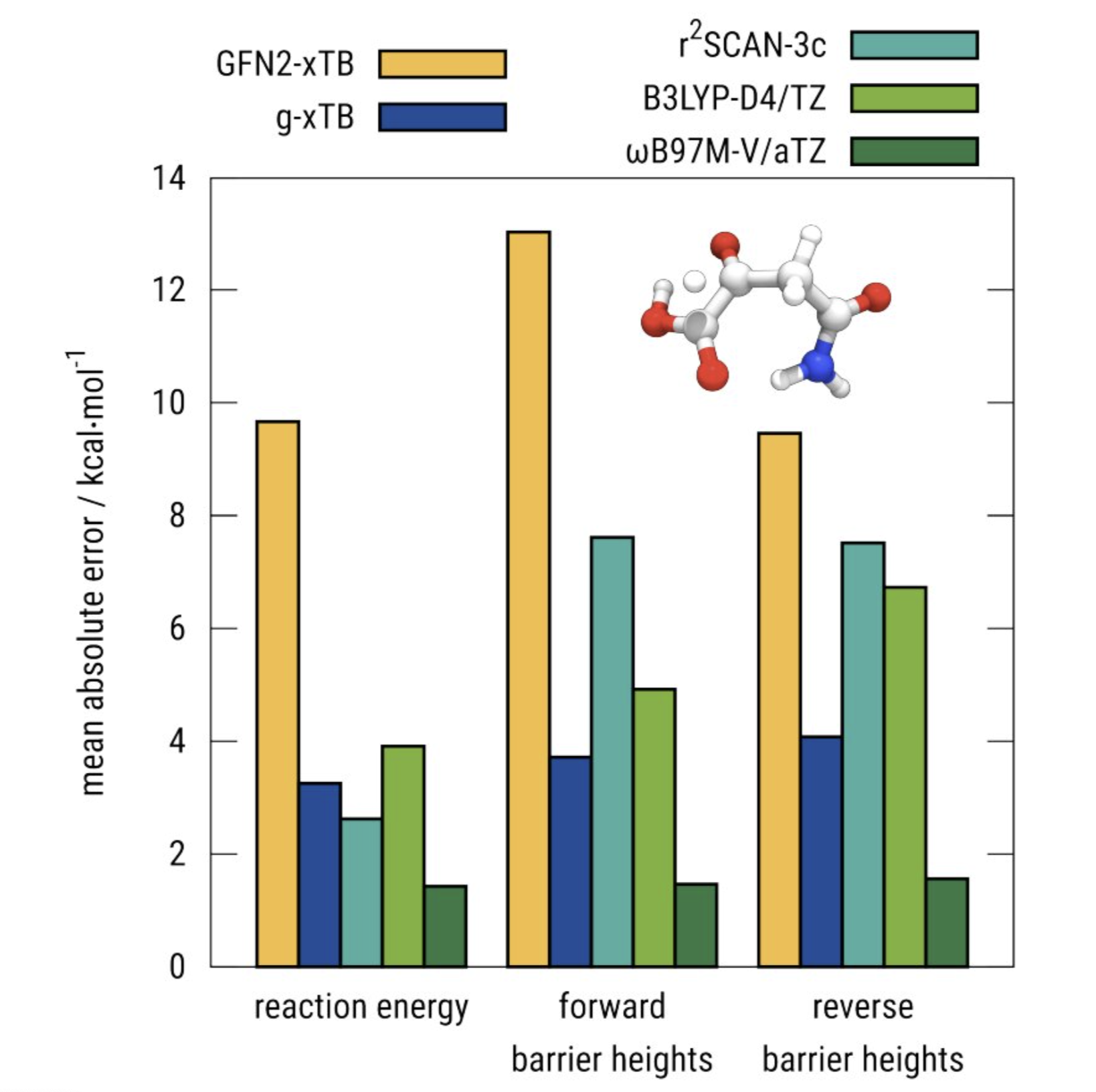
g-xTB is much better at predicting barrier heights.
g-xTB fixes the HOMO–LUMO gap issues exhibited by previous xTB methods and outperforms r2SCAN- or B3LYP-based methods at this task, a testament to the importance of range separation. This is particularly impactful since neural network potentials generally don't predict orbital energies or other electronic-structure properties.
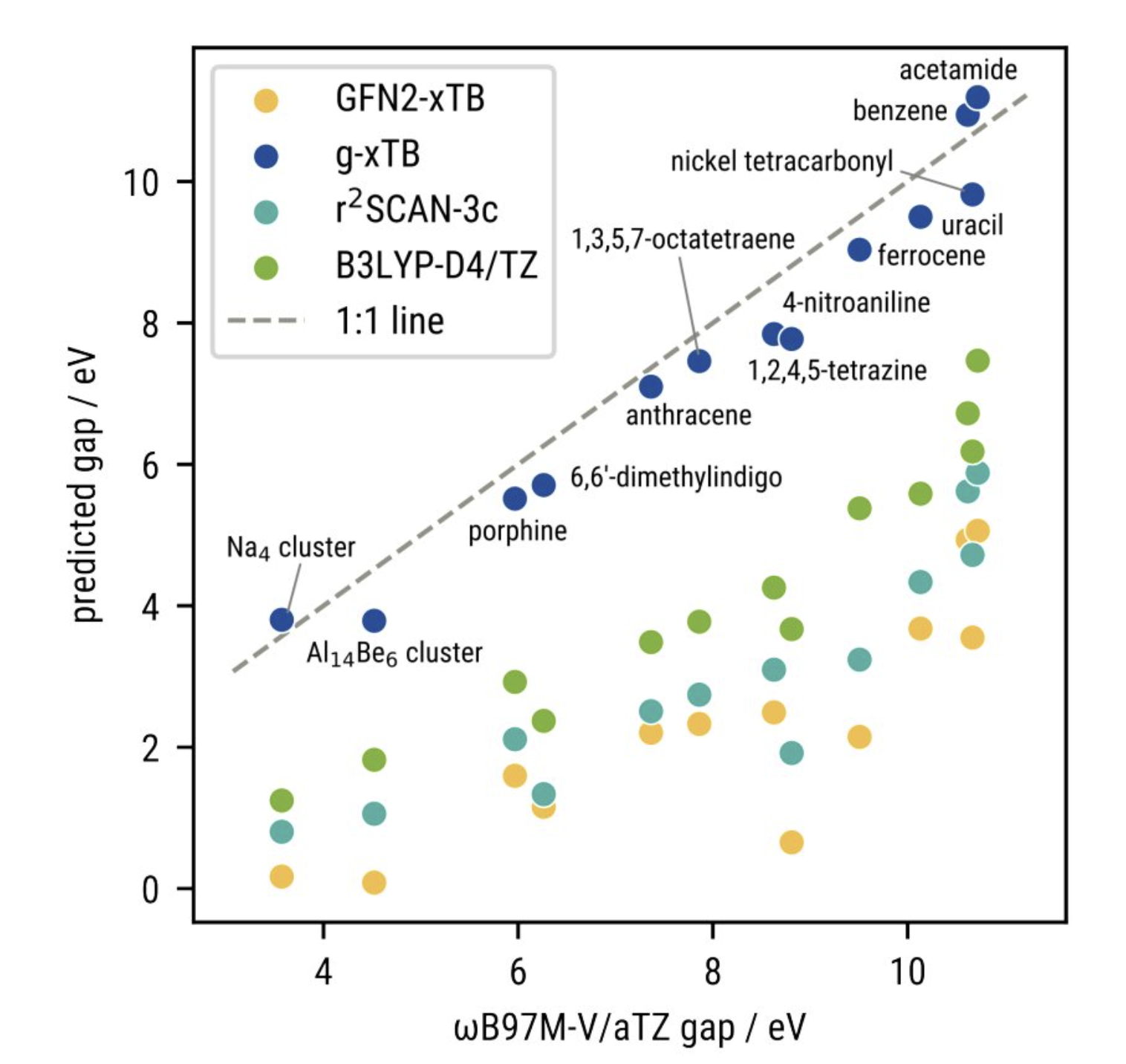
g-xTB fixes the orbital-energy issues seen with previous xTB methods.
Improvements are also seen beyond single-point properties. More reliable and accurate geometries are seen across a variety of transition-metal complexes, meaning that g-xTB can be used in combination with single-point DFT or wavefunction-based methods for more accurate energies.
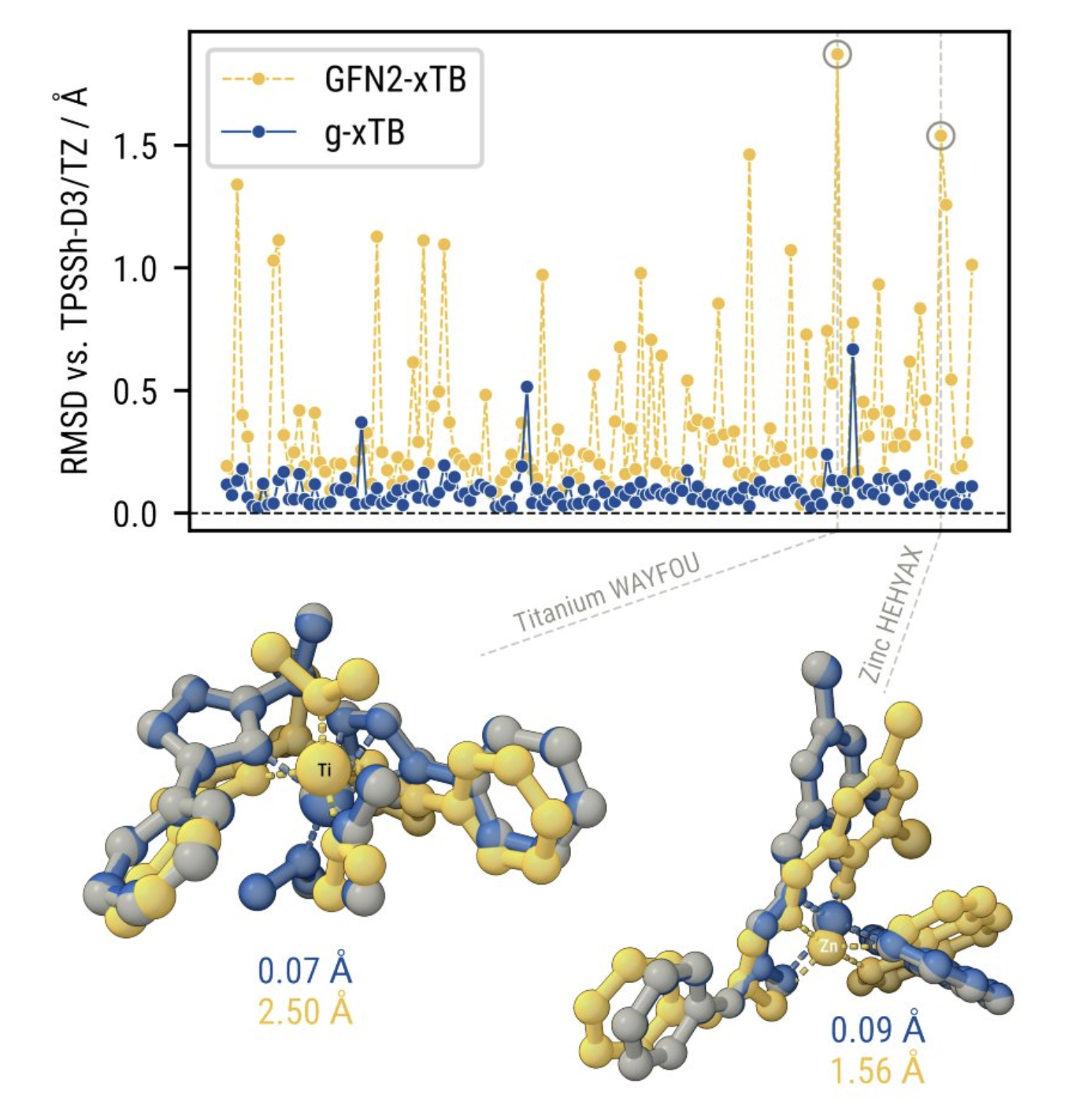
g-xTB gives better geometries than GFN2-xTB for transition-metal complexes.
Crucially, g-xTB accomplishes all this without being significantly slower than GFN2-xTB. In general, g-xTB is only a little slower than g-xTB (30% or less), making it essentially a drop-in replacement for any routine usage. (Note that the current release of g-xTB lacks analytical gradients, making geometry optimizations and frequency calculations significantly slower than GFN2-xTB or other low-cost methods.)
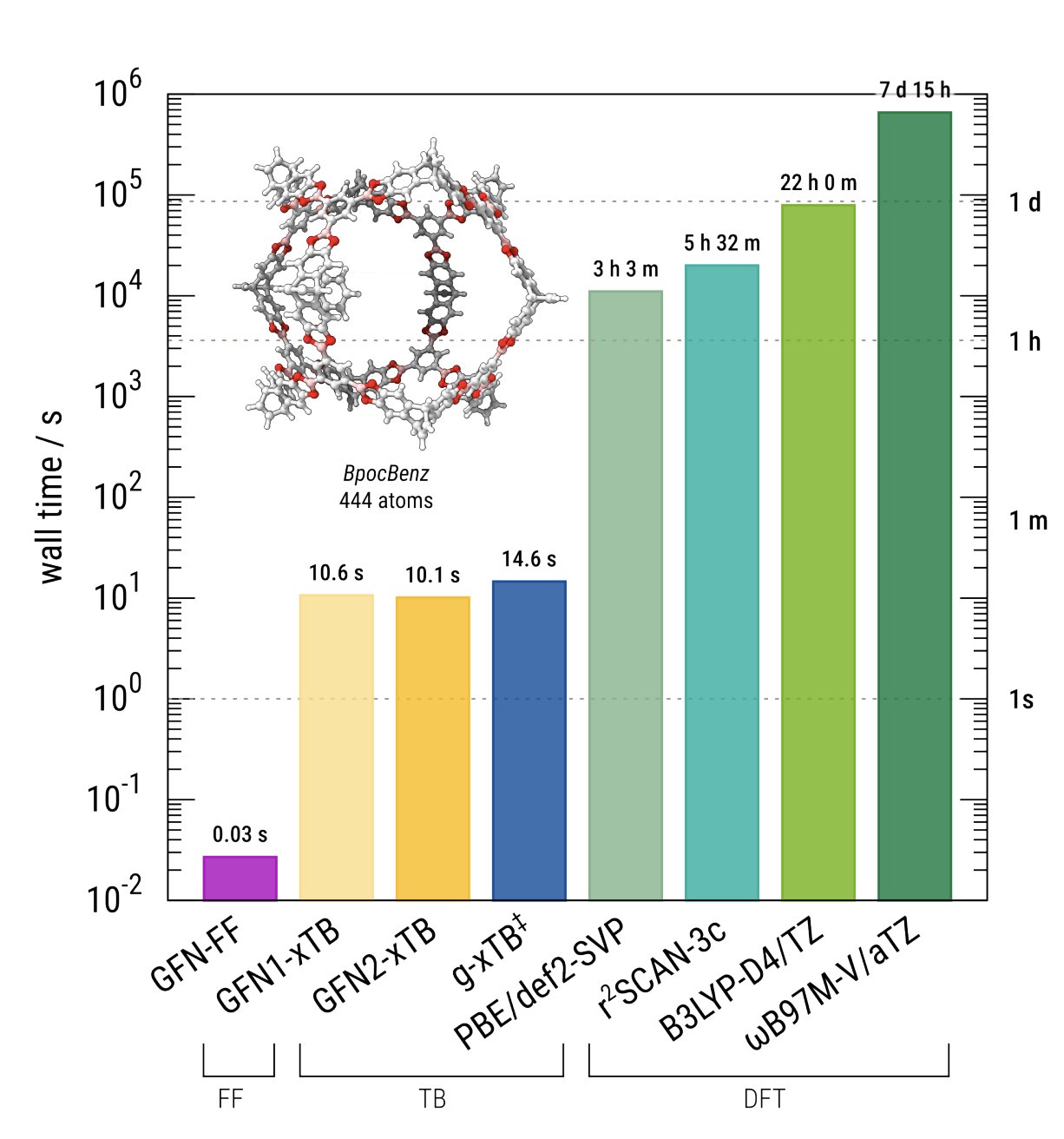
g-xTB is only a little slower than GFN2-xTB.
Applications
Routine Usage
For workflows where GFN-xTB has been "good enough," g-xTB can probably serve as a drop-in replacement with increased accuracy for virtually no increase in cost. For workflows where GFN-xTB has been a source of systematic bias—especially those involving barriers, redox potentials, or d-block chemistry—g-xTB will likely reduce but not eliminate the need for higher-level recalculation.
Bond-Dissociation Energy
g-xTB was found to be the best-performing methods at predicting bond-dissociation energy on a recent set of experimental C–H and C–X benchmarks. After linear correction g-xTB gave a mean absolute error (MAE) of 3.96 kcal/mol, far better than GFN2-xTB (7.88 kcal/mol) and comparable to the error of top DFT methods or neural network potentials. g-xTB//GFN2-xTB emerged as one of the two Pareto-dominant methods and is recommended for production usage when efficiency is at a premium.
GFNn-xTB predictions are poor, having significant scatter, while g-xTB calculations are strongly correlated to the experimental BDE.
Protein–Ligand Interaction Energies
The speed of g-xTB enables it to be used for systems outside the reach of conventional DFT methods, like large protein–ligand interactions. Benchmark results on the PLA15 dataset show that g-xTB outperforms other low-cost methods, including state-of-the-art neural network potentials like eSEN-OMol25-sm-conserving and UMA-S.
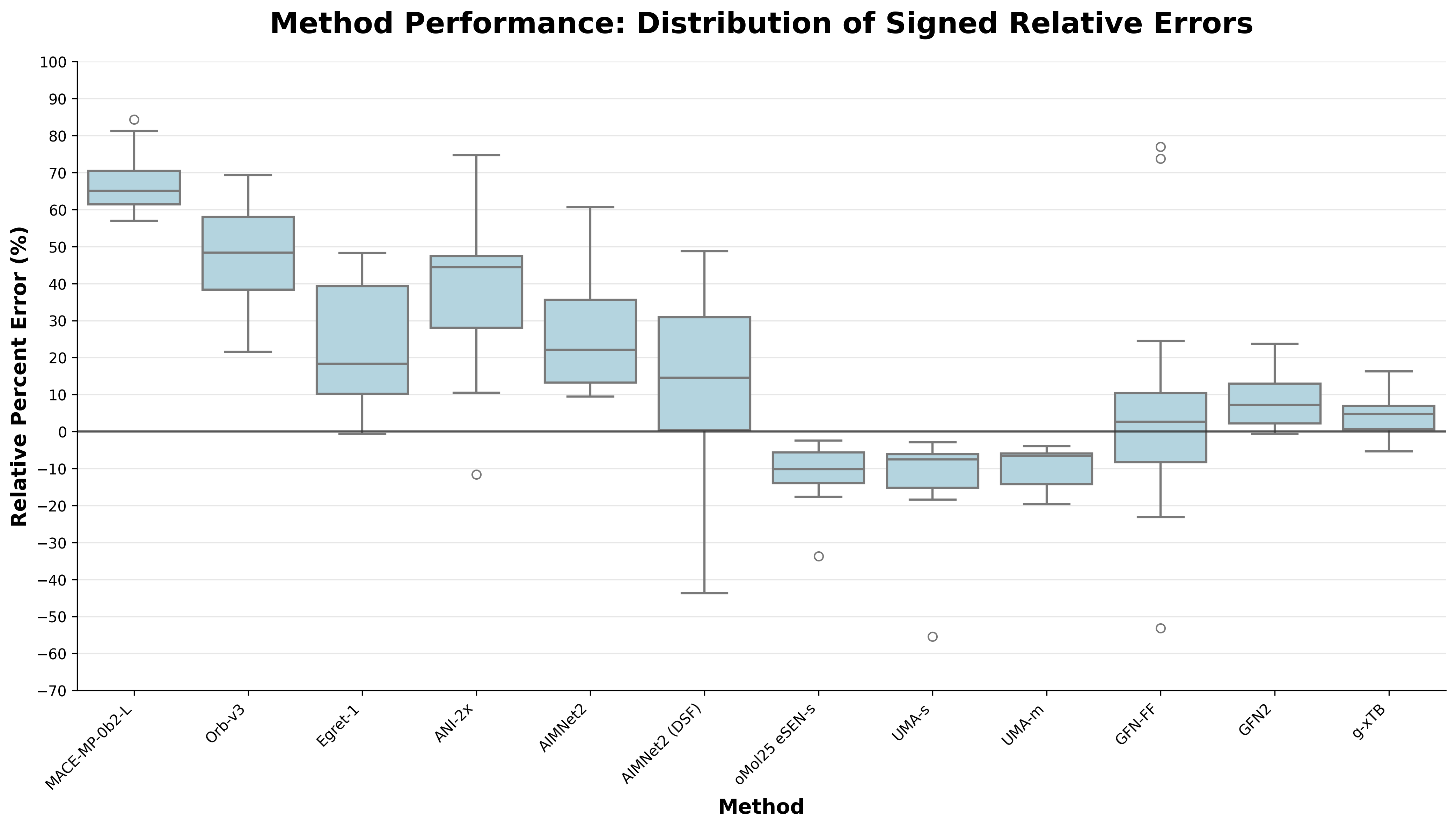
Comparison of the overall performance of different low-cost methods on the PLA15 benchmark, with g-xTB (right) performing best.
Conclusion
If the purpose of a general-purpose semiempirical method is to be the default quantum engine for geometry optimization, prescreening, and large-scale exploration, g-xTB looks like a plausible candidate. It is faster than DFT by orders of magnitude, more transferable than most ML models, and significantly more accurate than the GFN-xTB methods it is intended to replace.
While g-xTB sometimes underperforms NNPs on benchmarks, the physical underpinnings of the method seem to allow it to generalize better for out-of-distribution cases like large protein–ligand interactions. If you're working on modeling organic or inorganic chemistry, consider trying out g-xTB on Rowan today!
