ExpBDE54: A Slim Experimental Benchmark for Exploring the Pareto Frontier of Bond-Dissociation-Enthalpy-Prediction Methods
ExpBDE54 is a benchmark dataset of experimental homolytic bond-dissociation enthalpies (BDEs) for 54 small molecules. Single-point energies were computed using density-functional theory, semiempirical methods, and neural network potentials; linear regression corrections were applied to capture enthalpic effects. g-xTB//GFN2-xTB and OMol25's eSEN Conserving Small define the Pareto frontier, yielding root-mean-square errors of 4.7 and 3.6 kcal⋅mol–1. These results demonstrate that suitably corrected semiempirical and machine-learning approaches can enable rapid, accurate BDE predictions.
This preprint and the supporting information can also be viewed on ChemRxiv shortly.
Introduction
The strength of covalent bonds is one of the most fundamental properties in organic and inorganic chemistry, and understanding the strength of different bonds can allow scientists to predict the rate and thermochemistry of free-radical reactions and the regioselectivity of complex chemical processes. In synthetic chemistry, bond strengths are often employed to predict the regioselectivity of C–H functionalization reactions;1–3 in drug discovery, the strength of different bonds can be used to predict potential sites of metabolism.4,5
Unfortunately, experimental determination of bond strength is difficult, requiring careful gas-phase radical kinetics, photoionization mass spectrometry, or construction of acidity/electron affinity thermodynamic cycles (where applicable).6 None of these techniques are particularly amenable to high-throughput experimentation or routine usage; as such, computational prediction of bond-dissociation enthalpy (BDE) has become the dominant way by which bond strengths are prospectively estimated.
Despite the importance of computational methods for BDE predictions, most BDE benchmarks focus on narrow regions of chemical space, like metal–O2 bonds,7 bonds to nitro groups,8 aromatic–halogen bonds,9 bonds to silicon,10 peroxide bonds,11 fifth-row elements,12 aromatic–hydrogen bonds,13 and ylidic bonds.14 This diverse litany of benchmarks makes it difficult to assess which method is likely to perform best across a wide variety of structural features. Additionally, most of these studies predate the development of low-cost computational methods like neural network potentials, g-xTB, and r2SCAN-3c, leaving the relevance of these methods to BDE prediction an open question for the modern quantum-chemistry practitioner.15–17
In 2021, Viki Prasad and co-workers published the BSE49 benchmark set, which comprises 4,502 bond-separation-energy values computed at the (RO)CBS-QB3 level of theory. While this benchmark set is likely to be highly valuable for benchmarking new density functionals and basis sets, the authors note that these values are “differences between non-relativistic ground-state energies and contain no vibrational energy contributions, no zero-point energies,” and no conformational contributions, meaning that “the reported BSEs are not comparable to experimental BDEs.” We envisioned that a dataset of experimental BDE values might complement the BSE49 work and provide application-focused scientists a way to compare different end-to-end BDE-prediction workflows.
In this work, we report a new benchmark set of carbon–hydrogen and carbon–halogen BDE values, ExpBDE54, which is compiled from experimental gas-phase BDE measurements. We then evaluate various computational workflows against this benchmark set; our specific goal is not to maximize the accuracy of theoretical methods for BDE calculation, which has been studied by previous authors,18,19 but instead to identify practical low-cost workflows that enable rapid BDE calculations on large systems. We find that OMol25's eSEN Conserving Small20 is an effective method for medium-sized systems, that g-xTB//GFN2-xTB15,21 can be used when on CPU and speed is at a premium, and that r2SCAN-3c//GFN2-xTB21,22 represents the best speed/accuracy tradeoff for a QM-based method. We demonstrate the application of these workflows to predicting sites of CYP450 drug metabolism.4
Methodology
Dataset
We compiled ExpBDE54 from BDEs tabulated by Blanksby & Ellison,6 Yu-ran Luo,23 and Bordwell et al.24 ExpBDE54 is a small benchmark set designed to cover the chemical bonding motifs most relevant for practical problems in organic and medicinal chemistry. As such, the set almost entirely comprises carbon–hydrogen and carbon–halogen bonds.
While the small size of this dataset precludes many applications, like training machine-learning models, we anticipate that this can serve as an external "slim" benchmark25 for future method-development efforts.
The full benchmark set, composed of 54 SMILES strings and corresponding BDE values, is available in the Supporting Information.
Figure 1. ExpBDE54 molecules and experimental bond-dissociation enthalpies (kcal⋅mol–1).
Calculations
Initial structures were generated from SMILES and optimized with GFN2-xTB to serve as a starting point for all subsequent calculations. To calculate the electronic bond-dissociation energy (eBDE), the initial structure was optimized with the target method and then the chosen bond was cleaved homolytically, creating two doublet fragments. Fragments with more than one atom were optimized, and the eBDE was calculated as the electronic-energy difference between the molecule and its fragments. A linear regression was fit to the eBDEs relative to experimental bond-dissociation enthalpies (BDE) to correct for the lack of zero-point energy, enthalpy, and relativistic effects.
GFNn-xTB calculations were performed with xtb 6.7.1. g-xTB calculations were performed with a preliminary version of g-xTB that lacked analytic gradients.15
DFT calculations were performed with Psi4 1.9.1 (conda version: py312ha9da0b5_7).26 DFT calculations employed density fitting, a (99, 590) integration grid with "robust" pruning, the Stratmann–Scuseria–Frisch quadrature scheme, an integral tolerance of 10–14, and a level shift of 0.10 Hartree. r2SCAN-3c calculations employed a mTZVPP basis set, while all other DFT calculations employed the vDZP,27 def2-TZVPPD28,29 or def2-QZVP30 basis set (see Figure 2). All DFT calculations employed dispersion corrections in the form of D3BJ31 or D4.32
Geometry optimizations were run using geomeTRIC 1.1 (conda version: pyhd8ed1ab_1).33 Methods that employed different methods for optimization and single-point energies are denoted using double slash notation where relevant (single point//optimization).
All calculations were performed with the Rowan scientific platform on 4 cores of an AMD Ryzen 9 7950X3D (5.759 GHz) with multithreading turned off and 64 GB RAM running Ubuntu 24.04. Timings are reported as the total wall-clock time to run all calculations.
| Method/Functional | Class | Program |
|---|---|---|
| GFN0-xTB34 | Semiempirical | xtb |
| GFN1-xTB35 | Semiempirical | xtb |
| GFN2-xTB21 | Semiempirical | xtb |
| g-xTB15 | Semiempirical | gxtb |
| B3LYP-D432,36–39 | Hybrid DFT | Psi4 |
| r2SCAN-D416,32 | mGGA DFT | Psi4 |
| r2SCAN-3c22 | mGGA DFT | Psi4 |
| ωB97X-3c27 | RSH-GGA DFT | Psi4 |
| ωB97M-D3BJ31,40 | RSH-mGGA DFT | Psi4 |
| DSD-BLYP-D3BJ31,41 | DH-GGA DFT | Psi4 |
| eSEN-S20 | NNP | – |
| UMA-S42 | NNP | – |
| UMA-M42 | NNP | – |
| Basis Set | ζ |
|---|---|
| vDZP27 | 2 |
| mTZVPP22 | 3 |
| def2-TZVPPD28,29 | 3 |
| def2-QZVP30 | 4 |
Table 1. Methods and basis sets used in this study,
Results and Discussion
Density-Functional Theory
When it comes to calculating the properties of molecules of practical importance, density-functional theory (DFT) is often the most accurate method that can readily be applied to systems of interest. Calculation of eBDE with a variety of DFT functionals and basis sets showed a strong linear relationship with experimental BDE. r2SCAN-D4/def2-TZVPPD outperformed all other functional/basis set combinations, and a linear correction of the results lead to an RMSE of 3.6 with respect to the experimental BDEs (Figure 2). The larger def2-QZVP basis set had a negligible effect on the RMSE (and increased the computational time by 1.9x), indicating that the basis set limit with respect to BDE has likely been reached (attempts to utilize larger basis sets often led to SCF convergence issues). Moving to the vDZP basis, which was recently shown to be one of the most effective 2-ζ basis sets,43 led to a ≈1.5 kcal⋅mol–1 increase in the RMSE and a 2x increase in speed (Figure 3 and Table A1).
Other functionals showed only slightly lower accuracy with the same def2-TZVPPD basis set, with ωB97M-D3BJ/def2-TZVPPD seeing and increases in the RMSE by 0.1 kcal⋅mol–1 and B3LYP-D4/def2-TZVPPD increasing the RMSE by 0.46 kcal⋅mol–1 (while speeding up the calculation 2x). However, upon moving to the smaller vDZP basis set, the spread in the RMSE increased and ωB97M-D3BJ/vDZP become the most accurate method.
The specially constructed r2SCAN-3c “Swiss-army knife” method, with its tailor-made 3-ζ Gaussian basis, refit D4 correction, and geometrical counter-poise correction, was more accurate than any 2-ζ method, while offering a similar 2.5x speedup over r2SCAN-D4/def2-TZVPPD.
Given the small effect of switching functional and the lack of benefit of going to a larger basis, it is likely the methods are approaching the limit of accuracy achievable with purely the electronic energy. More accurate methods for prediction of BDE will likely require expensive enthalpy calculations or the use of group-specific corrections to the linear regression.
Figure 2. Calculated r2SCAN-D4/def2-TZVPPD eBDE vs experimental BDE.
Figure 3. Accuracy vs speed of BDE methods showing the Pareto frontier mostly occupied by 3-ζ basis methods.
DFT//GFN2-xTB
Optimization time accounts for >90% of the total time spent in the calculation of eBDE with DFT. In order to accelerate quantum-chemical calculations, it is common to use a more approximate method for the geometry-optimization step, since the error in the energy is second order with respect to errors in the geometry at stationary points. Swapping out the DFT optimization with GFN2-xTB yields almost identical results, the single outlier being H-atom removal from the carboxylic acid group in acetic acid. GFN2-xTB predicts a 143.0° O–C–O bond angle upon H-atom removal, as opposed to 111.5° from r2SCAN-D4/def2-TZVPPD (and 111.8° from high-accuracy RCCSD(T)-F12/CBS calculations44), leading to a 10 kcal⋅mol–1 error in the predicted eBDE (Figure 5). Optimization with g-xTB yields a 111.7° O–C–O bond angle; once analytic gradients become available, g-xTB is likely a better choice for optimization method. Despite the carboxyl-group outlier, switching to GFN2-xTB yields a significant increase in speed with negligible change in accuracy (Figure 4).
ωB97M-D3BJ/def2-TZVPPD//GFN2-xTB struggled with hexafluorobenzene. The original DIIS-based SCF convergence procedure predicted an energy 36 kcal⋅mol–1 too high for the pentafluoro fragment, and second-order SCF (SOSCF) was required to converge it to the correct state. This is likely a pathological case due to the symmetry and highly-electron-withdrawing nature of the system and should not be a significant issue with most calculations.
Figure 4. Optimization with GFN2-xTB as opposed to r2SCAN-D4/def2-TZVPPD has minimal effect on the resulting eBDE.
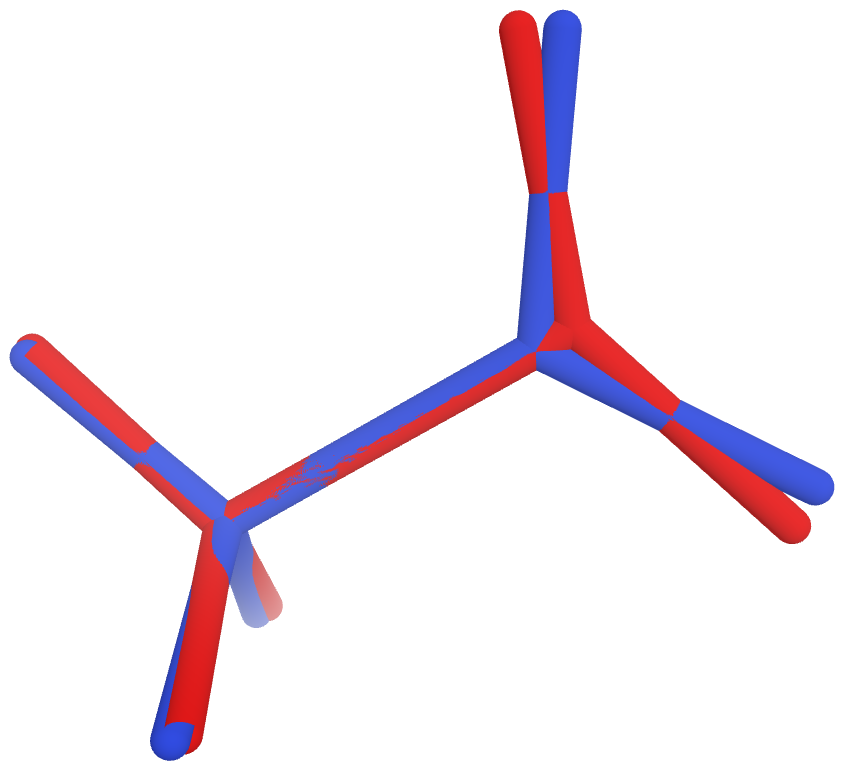
Figure 5. Carboxyl radical geometries showcasing erroneous O–C–O bond angle in GFN2-xTB (red) vs r2SCAN-3c (blue)
Figure 6. Optimization with GFN2-xTB leads to a significant increase in speed, with negligible loss in accuracy (though ωB97M-D3BJ/def2-TZVPPD required SOSCF for hexafluorobenzene fragmentation)
xTB Methods
Large-scale screening of molecules requires significantly faster methods for determination of BDEs. Semiempirical methods can accelerate geometry optimizations with minimal loss in accuracy, but their electronic energies are often more suspect. Indeed, BDEs calculated with GFN1-xTB and GFN2-XTB both have RMSEs about double that of DFT. Their predictions vary considerably (Figure 8), and while the linear corrections have similar slopes they are significantly offset (Figure 7). GFN0-xTB fairs poorly—the geometries were very similar to the other GFN-xTB methods, but the energies varied wildly.
However, the recently released g-XTB performs extremely well, being competitive with 2-ζ basis DFT but orders of magnitude faster. g-xTB is significantly slower than GFN2-xTB due to its current lack of analytic gradients, but combined g-xTB//GFN2-xTB calculations showed similar accuracy to pure g-xTB (Figure 8) and were only marginally slower than pure GFN2-xTB.
Figure 7. GFNn-xTB predictions are poor, having significant scatter. g-xTB calculations are strongly linearly correlated to the experimental BDE.
Figure 8. The GFN1-xTB and GFN2-xTB predicted eBDE values differ strongly, but the linear corrections vary by a constant.
Figure 9. Accuracy vs speed of BDE methods showing almost complete Pareto dominance by g-xTB//GFN2-xTB.
Neural Network Potentials
Neural network potentials (NNPs) can provide significantly faster energies and gradients than DFT while being much more accurate than semiempirical methods. Until recently, most NNPs were not trained on open-shell systems or only with small-basis non-hybrid DFT. The recently released OMol25 dataset contains more than 100 million density functional theory (DFT) calculations at the ωB97M-V/def2-TZVPD level of theory.20 We benchmarked three NNPs:
- OMol25's eSEN Conserving Small (hereafter eSEN-S)20
- UMA Small 1.1 (hereafter UMA-S)42
- UMA Medium 1.1 (hereafter UMA-M)42
The eSEN model is an equivariant graph transformer with spherical convolutions instead of attention and is trained on the OMol25 dataset.20 UMA models are mixture-of-experts variants of eSEN, additionally trained on OC20,45 ODAC23,46 OMat24,47 and OMC25,48 and utilize the OMol task.20,42 These methods are many orders of magnitude faster than DFT, are parameterized for the first 83 elements, and can take into account charge and spin, unlike most current NNPs.
eSEN-S results mostly mirror the ωB97M-D3BJ/def2-TZVPPD results from this study (due to the OMol25 dataset being calculated with ωB97M-V/def2-TZVPD). eSEN-S is 137x faster and has an RMSE of only 3.56 kcal⋅mol–1. The predictions of the two models were typically within 0.1 kcal⋅mol–1, with ωB97M-D3BJ/def2-TZVPPD vastly overpredicting the BDE for H-atom abstraction from acetone (103, 113), and eSEN-S underpredicting the terminal atom abstractions of triply bonded species (N≡C–H, H–C≡C–F, H–C≡C–H) by a few kcal⋅mol–1. UMA-S and UMA-M are larger than eSEN-OMol25 and are thus 3x and 17x slower. The more accurate UMA-M closely recapitulates ωB97M-D3BJ/def2-TZVPPD, avoiding the outliers seen with eSEN-S but gives a similarly incorrect BDE for acetone, leading to a marginally worse RMSE of 3.65 kcal⋅mol–1.
The eSEN and UMA NNPs are more accurate than g-xTB//GFN2-xTB, but 3–50x slower due to being run on a CPU. Significant acceleration could be achieved by running in batch on a GPU; the present work can be viewed as a lower bound on the potential speed of ML-based methods.
Figure 10. eSEN-S and ωB97M-D3BJ/def2-TZVPPD predict similar eBDEs.
Figure 11. Accuracy vs speed of BDE methods. g-xTB//GFN2-xTB and eSEN-S Pareto dominate most methods.
Application
In 2012, Kurt Drew and Jóhannes Reynisson found that C–H BDEs were an "indispensable component" of building xenobiotic-metabolism models.4 In their study, they computed BDE through linearly scaled density-functional-theory calculations run at the B3LYP/6-311+G(2df,p)//B3LYP/6-31+G(d,p) level of theory (hereafter referred to as B3LYP†). We investigated the 22 compounds for which structures were given in the paper and predicted all C–H BDEs. Of the 10 structures where the B3LYP† predicted site of lowest BDE aligns with that of CYP450 metabolism, eSEN-S aligned on 9 of them, with the only disagreement being cortisol. (We note that Drew and Reynisson report a non-standard structure for cortisol, and are unclear whether the calculations were performed on the given structure or the canonical structure of cortisol—this may explain the disagreement.)
For the remaining 12 structures where the lowest B3LYP† predicted C–H BDE did not align with the site of CYP450 metabolism, eSEN-S predicted the same site in all but three cases (tamoxifen, beta-arteether, and domperidone). In each of these cases, the site predicted by B3LYP† was the next lowest site predicted by eSEN-S. Additionally, for the 12 incorrect predictions, B3LYP† on average predicted 3.75 sites with a BDE lower than that of the actual site of CYP450 metabolism, while eSEN-S was off by an average of only 2.58 sites (with aromatic CYP450 metabolism sites accounting for nearly half of the error). While neither B3LYP† or eSEN-S BDEs are a perfect predictor of CYP450 metabolism, these data indicate that eSEN-S-predicted BDEs can serve as a drop-in replacement for DFT-predicted BDEs in xenobiotic-metabolism models.
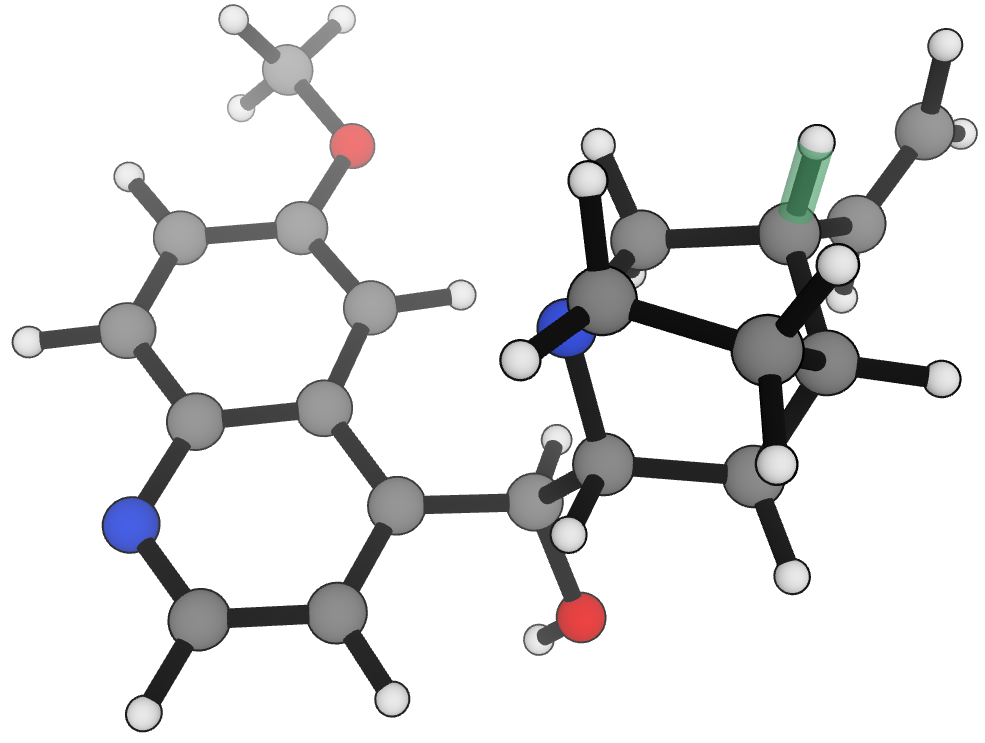
Figure 12. Lowest energy C–H BDE and site of CYP450 metabolism in quinidine.
Conclusion
We have introduced ExpBDE54, a slim benchmark of experimental gas-phase bond-dissociation enthalpies to aid in the development of computational bond-dissociation enthalpy workflows. Our results show that r2SCAN-D4/def2-TZVPPD//GFN2-xTB and eSEN-S achieve the lowest RMSE (both 3.56 kcal⋅mol–1), and further accuracy gains are likely limited without incorporation of enthalpy or group-specific corrections. The use of GFN2-xTB for optimization has negligible effect on the predicted values, and provides a ≈10x speedup for DFT-based methods. In this study, g-xTB//GFN2-xTB is slightly faster than eSEN-S due to the use of a CPU for all calculations, but use of a GPU and batching will allow eSEN-S to be significantly faster.
Taken together, our study clarifies the Pareto frontier for BDE calculations. eSEN-S nearly Pareto-dominates all methods, with fast and accurate BDE predictions. g-xTB//GFN2-xTB provides slightly faster results at the cost of a small decrease in accuracy, and r2SCAN-3c//GFN2-xTB offers the best mix of speed and accuracy among pure QM methods.
Appendix
| Method | Basis | Slope | Intercept | R2 | MAE | RMSE | Time |
|---|---|---|---|---|---|---|---|
| GFN0-xTB | 0.598 | 30.991 | 0.375 | 12.267 | 15.687 | 43.7 | |
| GFN1-xTB | 0.733 | -1.570 | 0.768 | 7.776 | 9.563 | 44.9 | |
| GFN2-xTB | 0.777 | 6.528 | 0.772 | 7.876 | 9.470 | 43.0 | |
| g-xTBa | 0.895 | 2.863 | 0.928 | 3.964 | 5.311 | 506.3 | |
| eSEN-S | 0.916 | 2.206 | 0.968 | 2.621 | 3.557 | 139.4 | |
| UMA-S | 0.916 | 2.026 | 0.963 | 2.830 | 3.798 | 407.9 | |
| UMA-M | 0.935 | 0.300 | 0.966 | 2.614 | 3.645 | 2424.0 | |
| B3LYP-D4 | vDZP | 0.899 | 7.456 | 0.923 | 4.233 | 5.510 | 5700.6 |
| B3LYP-D4 | def2‑TZVPPD | 0.928 | 3.080 | 0.958 | 2.931 | 4.083 | 9514.1 |
| r²SCAN-D4 | vDZP | 0.961 | 3.305 | 0.935 | 3.725 | 5.040 | 8225.8 |
| r²SCAN-3c | (mTZVPP) | 0.949 | 3.008 | 0.959 | 2.865 | 4.013 | 7141.6 |
| r²SCAN-D4 | def2‑TZVPPD | 0.976 | -0.118 | 0.967 | 2.624 | 3.607 | 19020.1 |
| r²SCAN-D4 | def2‑QZVP | 0.974 | 0.143 | 0.967 | 2.635 | 3.612 | 35708.1 |
| ωB97X-3c | (vDZP) | 0.891 | 4.762 | 0.942 | 3.564 | 4.794 | 5323.2 |
| ωB97M-D3BJ | vDZP | 0.928 | 0.871 | 0.948 | 3.346 | 4.508 | 8606.8 |
| ωB97M-D3BJ | def2‑TZVPPD | 0.922 | 1.838 | 0.965 | 2.585 | 3.712 | 19108.1 |
Table A1: BDE fitting parameters, errors (kcal⋅mol–1), and timings (seconds) for ExpBDE54.
aAnalytic gradients are not available for g-xTB
| Method | Basis | Slope | Intercept | R2 | MAE | RMSE | Time |
|---|---|---|---|---|---|---|---|
| GFN0-xTB | 0.593 | 31.441 | 0.372 | 12.319 | 15.725 | 46.8 | |
| GFN1-xTB | 0.727 | -0.880 | 0.762 | 7.847 | 9.687 | 46.9 | |
| GFN2-xTB | 0.777 | 6.528 | 0.772 | 7.876 | 9.470 | 43.0 | |
| g-xTB | 0.928 | -0.295 | 0.945 | 3.584 | 4.658 | 48.7 | |
| eSEN-S | 0.906 | 2.919 | 0.961 | 2.893 | 3.921 | 141.2 | |
| UMA-S | 0.910 | 2.399 | 0.962 | 2.888 | 3.863 | 335.4 | |
| UMA-M | 0.929 | 0.670 | 0.965 | 2.677 | 3.712 | 2026.9 | |
| B3LYP-D4 | vDZP | 0.888 | 8.247 | 0.922 | 4.257 | 5.548 | 774.3 |
| B3LYP-D4 | def2-TZVPPD | 0.923 | 3.414 | 0.958 | 2.854 | 4.073 | 1306.1 |
| r²SCAN-D4 | vDZP | 0.956 | 3.593 | 0.935 | 3.732 | 5.049 | 1054.8 |
| r²SCAN-3c | (mTZVPP) | 0.945 | 3.303 | 0.959 | 2.835 | 4.014 | 1061.2 |
| r²SCAN-D4 | def2-TZVPPD | 0.973 | -0.077 | 0.968 | 2.580 | 3.549 | 2403.7 |
| r²SCAN-D4 | def2-QZVP | 0.972 | 0.164 | 0.968 | 2.592 | 3.556 | 4180.3 |
| ωB97X-3c | (vDZP) | 0.883 | 5.291 | 0.939 | 3.674 | 4.891 | 790.5 |
| ωB97M-D3BJ | vDZP | 0.918 | 1.581 | 0.945 | 3.496 | 4.641 | 1021.2 |
| ωB97M-D3BJ | def2-TZVPPD | 0.916 | 2.251 | 0.963 | 2.685 | 3.797 | 2560.2 |
Table A2:GFN2-xTB geometry BDE fitting parameters, errors (kcal⋅mol–1), and timings (seconds) for ExpBDE54.,
- Garcia, Y. et al.. Theoretical bond dissociation energies of halo-heterocycles: Trends and relationships to regioselectivity in palladium-catalyzed cross-coupling reactions. Journal of the American Chemical Society 2009, 131, 18, 6632–6639.
- Liang, Y. et al.. A quantum chemistry study on C–H homolytic bond dissociation enthalpies of five-membered and six-membered heterocyclic compounds. Journal of the Indian Chemical Society 2022, 99, 7, 100527.
- Ji, Y. et al.. Origin of site-selectivity of hydrogen atom transfer in carbohydrate C–H alkylations via photoredox catalysis. Organic Chemistry Frontiers 2024, 11, 8, 2269–2276.
- Drew, K. L.; Reynisson, J.. The impact of carbon–hydrogen bond dissociation energies on the prediction of the cytochrome P450 mediated major metabolic site of drug-like compounds. European Journal of Medicinal Chemistry 2012, 56, 48–55.
- Zhao, S. et al.. Assessment of the metabolic stability of the methyl groups in heterocyclic compounds using C–H bond dissociation energies: Effects of diverse aromatic groups on the stability of methyl radicals. Journal of Physical Organic Chemistry 2005, 18, 4, 353–367.
- Blanksby, S. J.; Ellison, G. B.. Bond dissociation energies of organic molecules. Accounts of Chemical Research 2003, 36, 4, 255–263.
- Kosar, N. et al.. Benchmark density functional theory approach for the calculation of bond dissociation energies of the M–O₂ bond: A key step in water splitting reactions. ACS omega 2022, 7, 24, 20800–20808.
- Liu, J. et al.. Benchmark calculations and error cancelations for bond dissociation enthalpies of X–NO₂. Defence Technology 2023, 22, 144–155.
- Xu, S. et al.. Benchmark calculations for bond dissociation energies and enthalpy of formation of chlorinated and brominated polycyclic aromatic hydrocarbons. RSC Advances 2021, 11, 47, 29690–29701.
- Bari, A. et al.. Benchmark study of bond dissociation energy of SiX (XF, Cl, Br, N, O, H and C) bond using density functional theory (DFT). Journal of Molecular Structure 2017, 1143, 8–19.
- Carmona, D. J. et al.. DFT benchmark study of the O–O bond dissociation energy in peroxides validated with high-level ab initio calculations. Theoretical Chemistry Accounts 2020, 139, 7, 102.
- Badran, I. et al.. Bond dissociation energies of the fifth-row elements (In–I): A quantum theoretical benchmark study. International Journal of Quantum Chemistry 2023, 123, 23, e27222.
- Trung, N. Q. et al.. Calculating bond dissociation energies of X-H (X=C, N, O, S) bonds of aromatic systems via density functional theory: a detailed comparison of methods. Royal Society Open Science 2022, 9, 6, 220177.
- Zhao, Y. et al.. Benchmark database for ylidic bond dissociation energies and its use for assessments of electronic structure methods. Journal of Chemical Theory and Computation 2012, 8, 8, 2824–2834.
- Froitzheim, T. et al.. g-xTB: A General-Purpose Extended Tight-Binding Electronic Structure Method For the Elements H to Lr (Z= 1–103). DOI: 10.26434/chemrxiv-2025-bjxvt
- Furness, J. W. et al.. Accurate and numerically efficient r²SCAN meta-generalized gradient approximation. The Journal of Physical Chemistry Letters 2020, 11, 19, 8208–8215.
- Duignan, T. T.. The potential of neural network potentials. ACS Physical Chemistry Au 2024, 4, 3, 232–241.
- Menon, A. S. et al.. Bond dissociation energies and radical stabilization energies: An assessment of contemporary theoretical procedures. The Journal of Physical Chemistry A 2007, 111, 51, 13638–13644.
- Feng, Y. et al.. Assessment of experimental bond dissociation energies using composite ab initio methods and evaluation of the performances of density functional methods in the calculation of bond dissociation energies. Journal of Chemical Information and Computer Sciences 2003, 43, 6, 2005–2013.
- Levine, D. S. et al.. The Open Molecules 2025 (OMol25) Dataset, Evaluations, and Models. 2025. arXiv preprint arXiv:2505.08762 ,
- Bannwarth, C. et al.. GFN2-xTB—An accurate and broadly parametrized self-consistent tight-binding quantum chemical method with multipole electrostatics and density-dependent dispersion contributions. Journal of Chemical Theory and Computation 2019, 15, 3, 1652–1671.
- Grimme, S. et al.. r²SCAN-3c: A “Swiss army knife” composite electronic-structure method. The Journal of Chemical Physics 2021, 154, 6,
- Luo, Y.. Handbook of bond dissociation energies in organic compounds. Handbook of bond dissociation energies in organic compounds; CRC press:, 2002.
- Bordwell, F. G. et al.. Effects of adjacent acceptors and donors on the stabilities of carbon-centered radicals. Journal of the American Chemical Society 1992, 114, 20, 7623–7629.
- Gould, T.; Vuckovic, S.. “Slim“ benchmark sets for faster method development. Journal of Chemical Theory and Computation 2025,
- Smith, D. G. et al.. PSI4 1.4: Open-source software for high-throughput quantum chemistry. The Journal of Chemical Physics 2020, 152, 18,
- Müller, M. et al.. ωB97X-3c: A composite range-separated hybrid DFT method with a molecule-optimized polarized valence double-ζ basis set. The Journal of Chemical Physics 2023, 158, 1,
- Weigend, F.; Ahlrichs, R.. Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297. DOI: 10.1039/b508541a
- Rappoport, D.; Furche, F.. Property-optimized Gaussian basis sets for molecular response calculations. J. Chem. Phys. 2010, 133, 134105. DOI: 10.1063/1.3484283
- Weigend, F. et al.. Gaussian basis sets of quadruple zeta valence quality for atoms H–Kr. J. Chem. Phys. 2003, 119, 12753-12762. DOI: 10.1063/1.1627293
- Grimme, S. et al.. Effect of the damping function in dispersion corrected density functional theory. Journal of Computational Chemistry 2011, 32, 7, 1456–1465.
- Caldeweyher, E. et al.. A generally applicable atomic-charge dependent London dispersion correction. The Journal of Chemical Physics 2019, 150, 15,
- Wang, L.; Song, C.. Geometry optimization made simple with translation and rotation coordinates. The Journal of Chemical Physics 2016, 144, 21,
- Pracht, P. et al.. A robust non-self-consistent tight-binding quantum chemistry method for large molecules. DOI: 10.26434/chemrxiv.8326202.v1
- Grimme, S. et al.. A robust and accurate tight-binding quantum chemical method for structures, vibrational frequencies, and noncovalent interactions of large molecular systems parametrized for all spd-block elements (Z= 1–86). Journal of Chemical Theory and Computation 2017, 13, 5, 1989–2009.
- Becke, A. D.. Density-functional exchange-energy approximation with correct asymptotic behavior. Physical Review A 1988, 38, 6, 3098.
- Lee, C. et al.. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Physical Review B 1988, 37, 2, 785.
- Vosko, S. H. et al.. Accurate spin-dependent electron liquid correlation energies for local spin density calculations: a critical analysis. Canadian Journal of Physics 1980, 58, 8, 1200–1211.
- Stephens, P. J. et al.. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields. The Journal of Physical Chemistry 1994, 98, 45, 11623–11627.
- Mardirossian, N.; Head-Gordon, M.. Mapping the genome of meta-generalized gradient approximation density functionals: The search for B97M-V. The Journal of Chemical Physics 2015, 142, 7,
- Kozuch, S. et al.. DSD-BLYP: A general purpose double hybrid density functional including spin component scaling and dispersion correction. The Journal of Physical Chemistry C 2010, 114, 48, 20801–20808.
- Wood, B. M. et al.. UMA: A Family of Universal Models for Atoms. arXiv preprint arXiv:2506.23971 2025,
- Wagen, C. C.; Vandezande, J. E.. The vDZP Basis Set Is Effective For Many Density Functionals. arXiv preprint arXiv:2411.13253 2024,
- Kechoindi, S. et al.. Characterization and photochemistry of XCO2 (X= F, NH2, CH3) radicals. The European Physical Journal Special Topics 2023, 232, 12, 1905–1916.
- Chanussot, L. et al.. Open catalyst 2020 (OC20) dataset and community challenges. ACS Catalysis 2021, 11, 10, 6059–6072.
- Sriram, A. et al.. The Open DAC 2023 dataset and challenges for sorbent discovery in direct air capture. The Open DAC 2023 dataset and challenges for sorbent discovery in direct air capture; ACS Publications:, 2024.
- Barroso-Luque, L. et al.. Open materials 2024 (omat24) inorganic materials dataset and models. arXiv preprint arXiv:2410.12771 2024,
- Open Molecular Crystals 2025 (OMC25) dataset and models.
