Studying Scaling in Electron-Affinity Predictions
by Corin Wagen · Sept 10, 2025
Last week, we released a paper showing that OMol25-trained NNPs can accurately predict molecular properties that depend on the difference in energy between different charge and spin states, like reduction potential and gas-phase electron affinity. Across a wide variety of main-group and organometallic systems, we observed that NNPs could be used as a high-throughput way to predict these properties with good accuracy.
This result is surprising since the NNPs that we benchmarked don't actually compute any exact charge-related physics, they simply take "charge" as an input feature. Much ink has been spilled about how NNPs without explicit long-range physics will give incorrect predictions for charge-related properties (see my review here), and so we were surprised to see that the models performed just as well or better than conventional physics-based methods in our study.
Since these models were trained on so much data, it's possible that the observed good performance is simply a form of "memorization" and that non-physical behavior will occur as we scale to larger and larger systems. We discussed such a possibility in our conclusion:
Nevertheless, the OMol25 NNPs generally perform equivalently to or better than state-of-the-art semiempirical or low-cost DFT methods on the benchmark sets studied here. These results suggest that a lack of explicit physics does not significantly compromise OMol25 NNPs' ability to optimize and determine the energetics of structures in a variety of charge states for small systems. This study does not address condensed-phase effects or scaling to large systems; there may be emergent inaccuracies that arise from the lack of explicit physics at larger length scales.
If we're worried about scaling, why not test it directly? Unfortunately, it's not trivial to find a clean experimental test case for how redox-related properties scale; gas-phase comparisons are the cleanest, but gas-phase reference data is hard to measure and relatively sparse. Ideally a benchmark would include rather large systems where simple GNNs might break down, but we weren't able to find electron-affinity or ionization-potential data that we were happy with for large gas-phase systems. (We might be overlooking something!)
I still wanted to tackle this problem, though, so I decided to take a shot at informally modeling scaling effects with the best combination of experimental and computational data I could cobble together. I ended up looking at electron affinity for a series of linear acenes, from naphthalene (with two benzene rings) to the N=11 acene which is almost 30 Å long. I was able to find experimental reference data for naphthalene (N=2), anthracene (N=3), tetracene (N=4), and pentacene (N=5).
The N=11 acene, which is almost 30 Å long.
With a few experimental data points in hand, I next compared a bunch of different computational methods. Since there isn't experimental data for the whole series, we can't actually look at energy-based metrics like MAE or RMSE. Instead, the goal is just a qualitative comparison: what's the expected physics-based scaling relationship, and can NNPs predict the correct shape or not? (From first principles, we'd expect that larger molecules have a larger electron affinity.)
Calculations were run on optimized GFN2-xTB geometries. Here's the data:
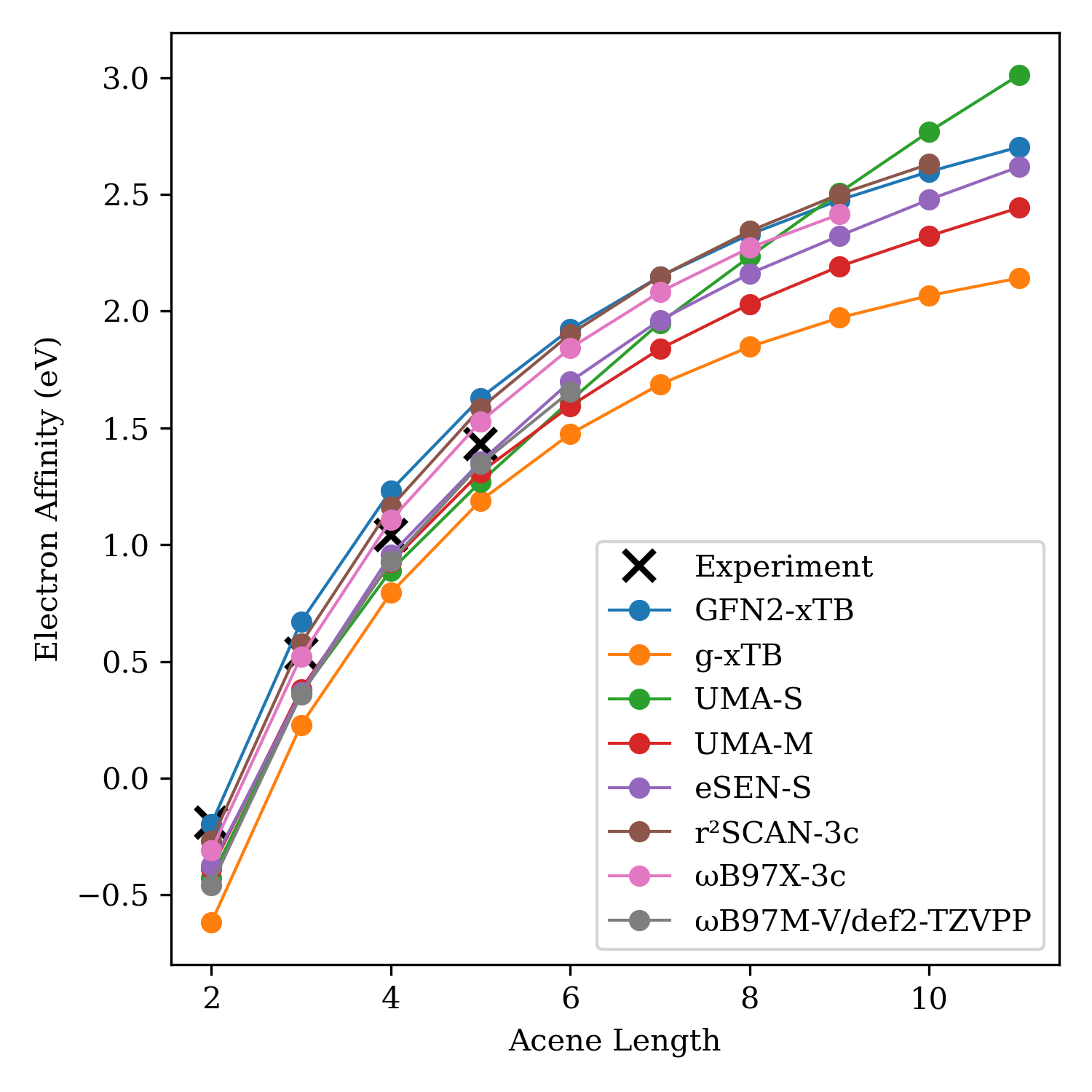
The match to experiment isn't perfect—we neglect frequencies here, which probably doesn't matter much but will change the results a little bit. Still, this data suggests that the NNPs are able to describe scaling just as well as the physics-based methods on this dataset (with the possible exception of UMA-S). Even though there isn't any explicit Coulombic interaction in the energy predictions, the NNPs correctly "understand" that larger acenes will have more delocalization and a higher electron affinity, which raises my confidence that these models aren't just memorizing everything but instead are building some chemical intuition.
(It's worth noting that the ωB97M-V/def2-TZVPP results aren't amazing here. The lack of diffuse functions probably plays a role here, as diffuse functions are almost always necessary for describing gas-phase anions like these. Previous work by Truhlar has shown that a high degree of basis-set augmentation is needed for accurate prediction of electron affinity.)
Here's the underlying data. Note that naphthalene has a negative electron affinity, but through experimental wizardry a value was still able to be measured.
| N | Exp. | GFN2-xTB | g-xTB | UMA-S | UMA-M | eSEN-S | r2SCAN-3c | ωB97X-3c | ωB97M-V/def2-TZVPP |
|---|---|---|---|---|---|---|---|---|---|
| 2 | -0.19 | -0.195 | -0.617 | -0.428 | -0.387 | -0.374 | -0.267 | -0.309 | -0.457 |
| 3 | 0.532 | 0.671 | 0.229 | 0.366 | 0.382 | 0.369 | 0.578 | 0.522 | 0.358 |
| 4 | 1.04 | 1.233 | 0.794 | 0.890 | 0.925 | 0.958 | 1.162 | 1.106 | 0.930 |
| 5 | 1.43 | 1.629 | 1.189 | 1.269 | 1.311 | 1.356 | 1.585 | 1.527 | 1.346 |
| 6 | 1.923 | 1.475 | 1.617 | 1.594 | 1.699 | 1.902 | 1.842 | 1.657 | |
| 7 | 2.149 | 1.687 | 1.950 | 1.839 | 1.962 | 2.149 | 2.083 | ||
| 8 | 2.329 | 1.848 | 2.234 | 2.031 | 2.161 | 2.343 | 2.272 | ||
| 9 | 2.476 | 1.972 | 2.508 | 2.192 | 2.323 | 2.501 | 2.415 | ||
| 10 | 2.598 | 2.067 | 2.769 | 2.322 | 2.478 | 2.630 | |||
| 11 | 2.703 | 2.142 | 3.011 | 2.443 | 2.618 |
And here's the script used to generate these results. The below code reads in xTB-optimized geometries from opt/ and submits single-point calculations on them, waits for the calculations to finish, and then prints the results. (This could definitely be made a bit cleaner if it were being reused; I include this code not because it's particularly elegant, but because it's emblematic of the sort of one-off scripts I often write using our API to solve problems.)
import rowan
import stjames
rowan.api_key = "rowan-sk-your-key-here"
nws = []
rws = []
# Submit each calculation and then save workflow object
for i in range(2, 12):
neutral_mol = stjames.Molecule.from_file(f"opt/{i}_neutral.xyz")
reduced_mol = stjames.Molecule.from_file(f"opt/{i}_reduced.xyz", charge=-1, multiplicity=2)
nw = rowan.submit_workflow(
initial_molecule=neutral_mol,
workflow_type="basic_calculation",
workflow_data={
"settings": {
"method": "wb97m-v",
"basis_set": "def2-tzvpp",
"tasks": ["energy"],
},
"engine": "psi4",
},
name=f"neutral sp {i}",
)
rw = rowan.submit_workflow(
initial_molecule=reduced_mol,
workflow_type="basic_calculation",
workflow_data={
"settings": {
"method": "wb97m-v",
"basis_set": "def2-tzvpp",
"tasks": ["energy"],
},
"engine": "psi4",
},
name=f"reduced sp {i}",
)
nws.append(nw)
rws.append(rw)
# Wait for all calculations to finish, then retrieve results
for i, (nw, rw) in enumerate(zip(nws, rws, strict=True)):
nw.wait_for_result()
nw.fetch_latest(in_place=True)
ne = rowan.retrieve_calculation_molecules(nw.data["calculation_uuid"])[-1]["energy"]
rw.wait_for_result()
rw.fetch_latest(in_place=True)
re = rowan.retrieve_calculation_molecules(rw.data["calculation_uuid"])[-1]["energy"]
# Convert from Hartree to eV
ea = (ne-re) * 27.2114
print(f"{ea:.3f}")
There's a lot more that could be done here: this is just one class of molecules and one property. Still, I think this data rules out worst-case scenarios where OMol25-based NNPs excel at tiny structures but catastrophically fail to generalize to anything larger than their training data.