The Multiple-Minimum Monte Carlo Method for Conformer Generation
by Nick Casetti · Nov 24, 2025
This is a guest post by Nick Casetti, the author of the multiple-minimum-monte-carlo package we use here at Rowan. Nick is a graduate student in the Coley Group at MIT; his research focuses on using machine-learned interatomic potentials to elucidate and explore reaction mechanisms.
When dealing with the 3D conformations of molecules, there is an important relationship between the ensemble of conformations accessible by that molecule and the properties we care about (enthalpy, Gibbs free energy, etc.). Many important molecular properties must be calculated as Boltzmann averages over the full conformer ensemble, making it vital to perform thorough and high-quality conformer searches. Unfortunately, due to compute constraints associated with quantum chemistry calculations, there are circumstances where researchers will calculate properties based on only a single conformation. The emergence of high-quality quantum chemistry datasets and machine-learned interatomic potentials (MLIPs) is helping to alleviate this compute bottleneck which means more rigorous conformer searches should become increasingly commonplace. To help drive this paradigm shift, open-source and easy-to-use tools must be developed to help chemists leverage the existing set of conformer search methods.
Many methods exist to evaluate the conformational space available to molecules. Molecular dynamics (MD) is a common way to understand typical conformational fluctuations but struggles to explore rare events that may be key to finding global minima. Metadynamics is a modified MD-based approach that accelerates exploration by biasing the simulation away from already seen conformations. This is a key part of the popular iterated metadynamics conformational search methods implemented in CREST. A different way to drive exploration is with random sampling. Random-sampling methods like Monte Carlo methods will randomly sample conformations, evaluate them, and determine whether to include them in the final ensemble based on some criteria. This blog post digs a little deeper into a Monte Carlo approach and where it's useful, but all of these methods have their place and should be selected based on problem settings.
I've recently adapted and implemented a multiple-minimum Monte Carlo sampling approach described by Chang et al. for use with any ASE calculator (a common interface for QM methods and MLIPs). This method randomly modifies an input molecule's dihedral angles to access new conformations. These conformations are first subject to a quick steric test to reject unphysical dihedral angle modifications and then a minimization is performed to move the conformation into the nearest energy minimum. This minimum is accepted or rejected based on an energetic and RMSD-based requirement. The energy minimum must be no greater than a specified energy window (a typical value is 10 kcal/mol) above the current global minimum energy. If this is true, the geometry is compared to the rest of the accepted geometries to determine whether it is a repeat (as measured by an RMSD threshold). If accepted, the conformer joins the ensemble and is used to accept/reject newly sampled conformers.
The input molecular conformation (the conformer whose dihedrals are modified for sampling) changes across the course of the run. This input is sampled from the conformer ensemble (which starts with just the original conformer). It can be sampled randomly, but it was found that "usage-directed" sampling results in more efficient sampling. "Usage-directed" sampling simply means using the conformer that has been used the least where ties are broken by energy; this is the default sampling strategy in my implementation. I've included a flow chart below as a visual breakdown of the method.
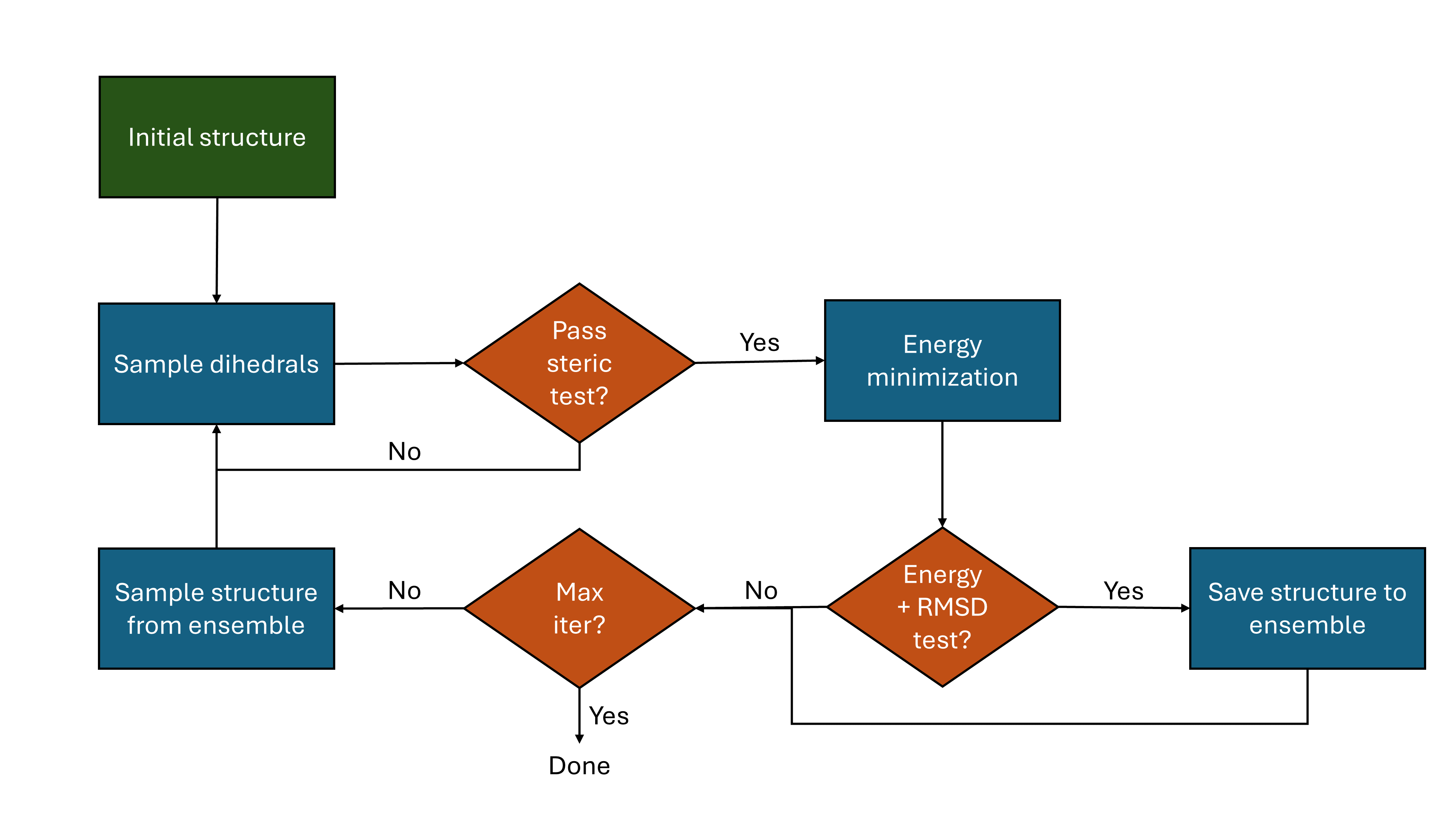
A visual overview of the multiple-minimum Monte Carlo algorithm.
One of the major applications I had in mind when I originally developed this implementation was finding accurate low-energy structures for the sorts of flexible structures and catalysts often relevant in homogenous catalysis. For large and flexible systems like the below dimeric hydrogen-bond-donor catalyst reported by Kennedy and co-workers, the multiple-minimum Monte Carlo (MMMC) method significantly outperforms the metadynamics-based methods implemented in CREST. Both methods were started from an extended conformation generated by RDKit: after only 250 iterations, the Monte Carlo method explores significantly more conformational space and locates a minimum-energy structure over 8 kcal/mol lower than the lowest-energy conformation from CREST. The diversity of conformers explored by the MMMC method makes it ideally suited for downstream reactivity modeling and completely changes the accessible substrate-binding modes.
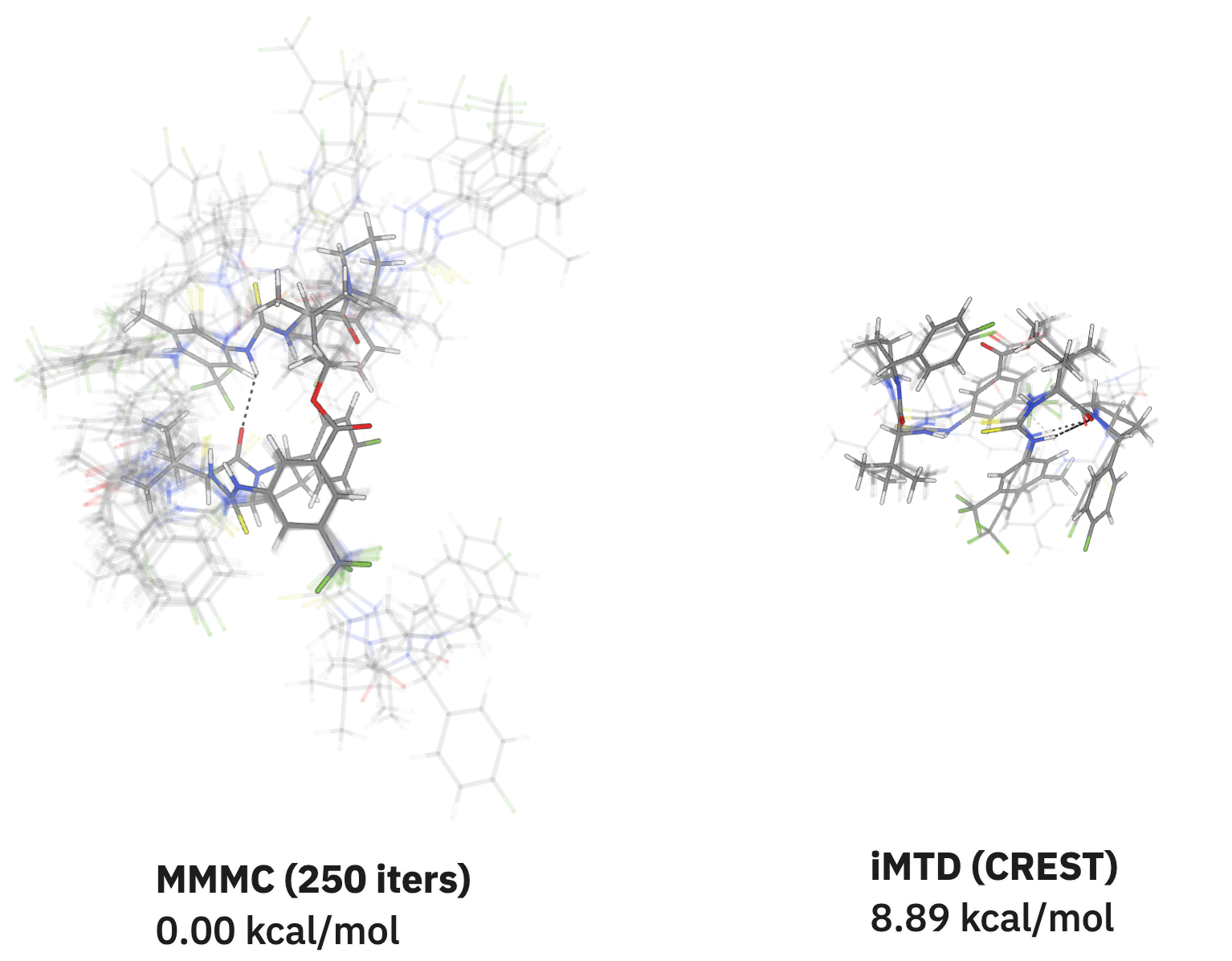
Comparison of MMMC with iMTD, showing that MMMC explores a larger space of conformers.
Robust exploration of relevant molecular conformations is key to the success of effective computational chemistry modelling and is likely to become more prevalent with the continued development of MLIPs. The Monte Carlo method presented here can help drive this exploration, particularly in flexible molecules.
This implementation supports a few extra features like freezing atoms, parallel or batched calculations for speed, and user-defined optimization routines; if any of this is of interest to you, please check out the GitHub and feel free to create issues, request features, or make pull requests at this repository, which will be actively maintained! And if you'd like to try out this conformer-search method without writing any code, check out Rowan's implementation!