How to Predict pKa
by Corin Wagen · Oct 16, 2025
Prediction of acid dissociation constants (pKa) is a ubiquitous task in computational drug discovery and materials science. Unfortunately, it's also very difficult. There are no perfect solutions to pKa prediction: instead, there are a plethora of different theoretical approaches, each with their strengths and weaknesses.
We often find that newcomers to the pKa-prediction field are confused by the variety of theoretical approaches used. To help make the advantages and disadvantages of different methods apparent, we've put together a quick overview of the different paradigms, with examples of each method (from us and from other groups) and links to key publications. This isn't intended to be a comprehensive review—rather, our goal is to help readers understand the field at a high level to better equip them to read the primary literature.
We've divided pKa-prediction methods into five high-level categories, each of which is explained below. One distinction that we're not making here is between microscopic and macroscopic pKa: while this matters a lot in practice, almost all of the below techniques can be applied to microscopic pKa prediction or macroscopic pKa prediction depending on how the input microstates are selected.
1. Quantum Mechanics
One of the most straightforward ways to compute pKa is simply to compute the difference in free energy between two microstates with a quantum-chemical method like density-functional theory (DFT). While naïve application of this strategy often leads to poor predictions owing to inaccuracies in commonly used continuum solvation models, linear or quadratic corrections can be used to dramatically improve agreement with experiment.
Different instantiations of this approach have been among the top-performing methods in pKa-prediction challenges like SAMPL6 and SAMPL7; in particular, since minimal fitting to experimental data is required, these approaches are very general and extrapolate well to new regions of chemical space.
The downside of this strategy is speed: consistent performance requires thorough conformer searching for each microstate and large numbers of geometry optimizations, which mean that a single microscopic pKa value can easily take hours or days of time even on high-performance computing infrastructure. Although in most cases these calculations can be parallelized, the cumulative complexity makes these calculations relatively expensive and ill-suited for high-throughput usage. (This is why Rowan's microscopic-pKa workflow uses the AIMNet2 neural network potential—the speed of AIMNet2 lets this quantum-chemical strategy run in minutes, not days.)
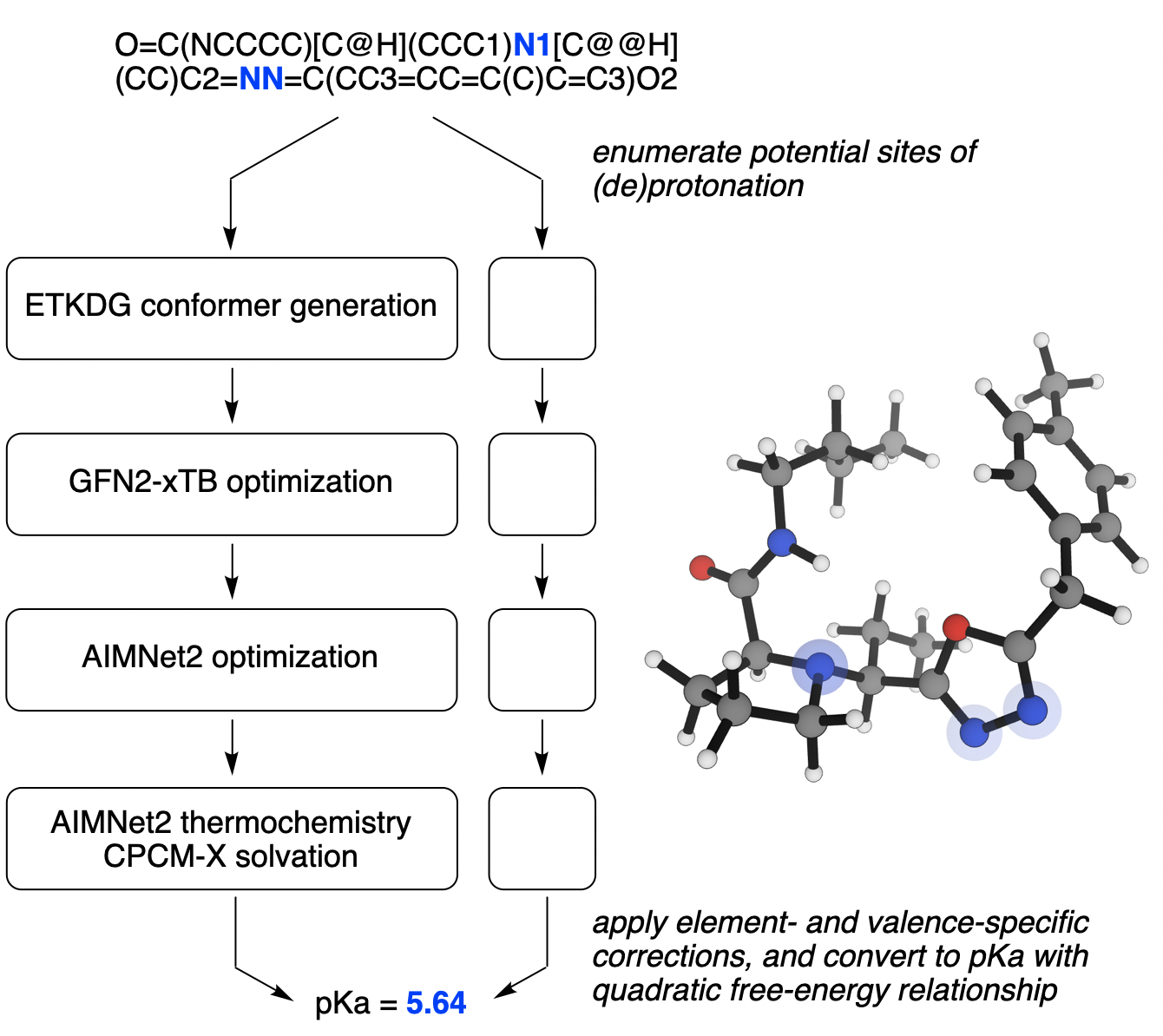
Visual overview of Rowan's AIMNet2-based workflow. Read the preprint here.
Applications:
- Schrödinger's Jaguar pKa
- Rowan's AIMNet2-based microscopic pKa workflow
- MOPAC's pKa functionality
Representative Publications:
- This paper from Schrödinger explains how their Jaguar pKa product works.
- This paper from Philipp Pracht and co-workers presents a straightforward workflow for QM-based pKa prediction.
- Rowan's preprint explains how we use AIMNet2 and semiempirical implicit-solvent models to accelerate DFT-based pKa workflows.
2. Explicit-Solvent Free-Energy Simulations
Explicit-solvent free-energy simulations can be used to more directly and accurately account for solvation effects. This can be done though a variety of approaches. Constant-pH molecular dynamics uses Monte Carlo- or λ-dynamics to model protonation state changes; this can then be used to fit titration curves and extract microscopic pKa values. In contrast, alchemical free energy methods use techniques like free-energy perturbation or thermodynamic integration to directly compute the free-energy difference between a conjugate acid–base pair.
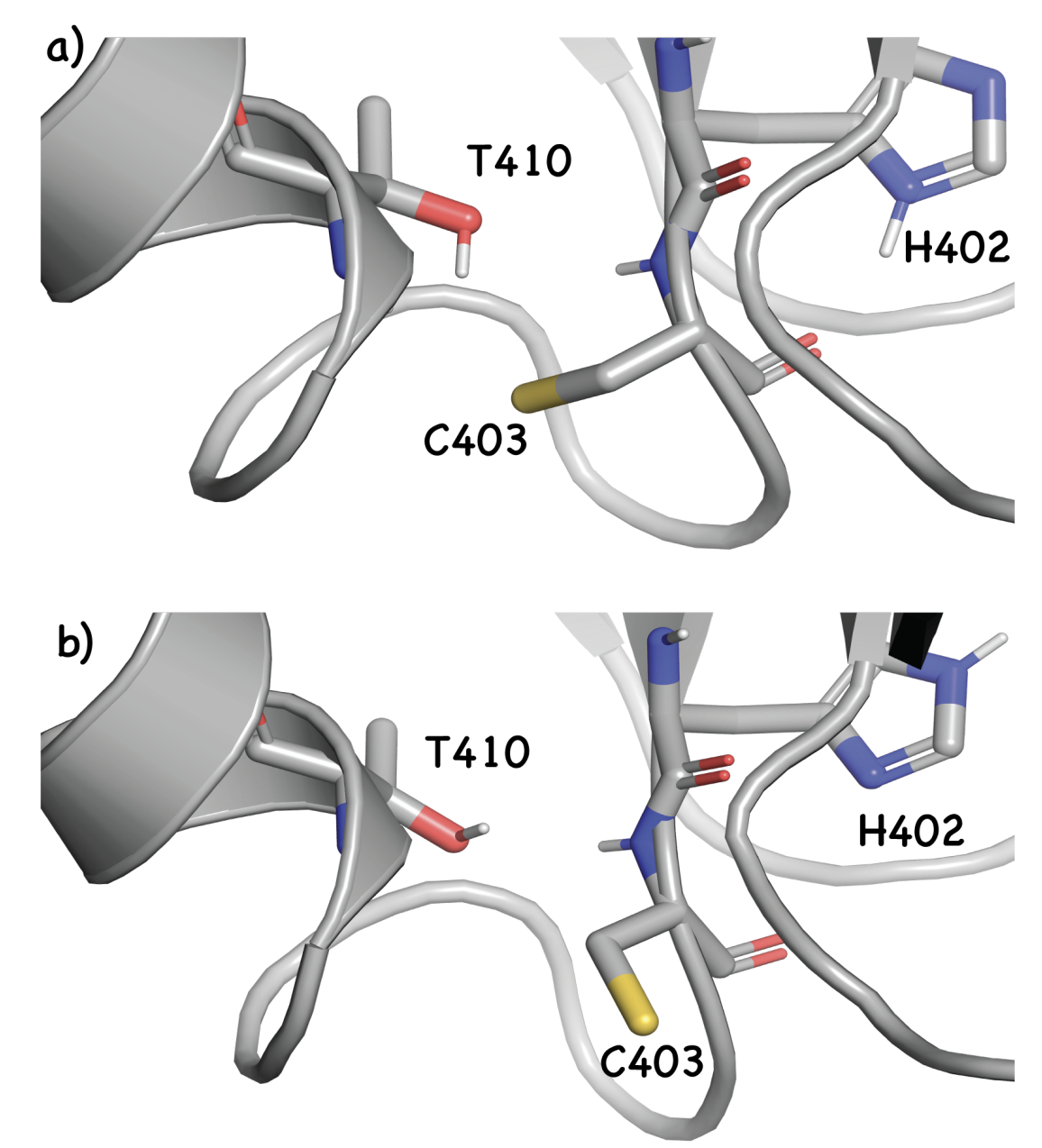
Representative conformations of a key Cys, illustrating how proper sampling is key for accurate protein pKa prediction. Image from Awoonor-Williams et al, 2023.
Like other free-energy methods, these calculations often end up being relatively expensive and (to our knowledge) are uncommonly employed in prospective drug-design work for small molecules. These methods see more use in protein pKa prediction, where direct QM-based workflows are generally impractical.
Applications:
- OpenMM, AMBER, CHARMM, NAMD, and other molecular dynamics engines all give users the ability to run constant-pH simulations.
- Schrödinger's FEP+ can be used to compute pKa values for protein residues.
Representative Publications:
- This seminal 1987 paper from Bill Jorgensen details how to use free-energy perturbation to predict the pKa of small organic molecules.
- This review from Pavel Buslaev and co-workers discusses best practices for constant-pH molecular dynamics.
- This paper from Dilek Coskun and co-workers details the use of FEP+ to predict protein pKa values.
3. Fragment- or Group-Based Methods
These models estimate pKa from substituent/fragment effects (Hammett/Taft-style linear free-energy relationships) and curated fragment libraries, often with expert-coded rules for resonance/field effects and tautomerism. These models are very fast and often extremely accurate within a given domain of applicability, but may generalize poorly and can also miss complex chemical motifs or through-space effects.
Applications:
- ACD/Labs' pKa module
- Schrödinger's Epik Classic
Representative Publications:
- This technical report from Advanced Chemistry Development explains the ACD pKa module and how it works.
4. Data-Driven Methods
Data-driven models learn pKa relationships from structure/features; they range from descriptor-based regressors to modern graph neural networks (GNNs) that predict site-level pKa. This category includes both descriptor-based QSPR models using classical features and deep graph-based models that learn atomic environment features directly.
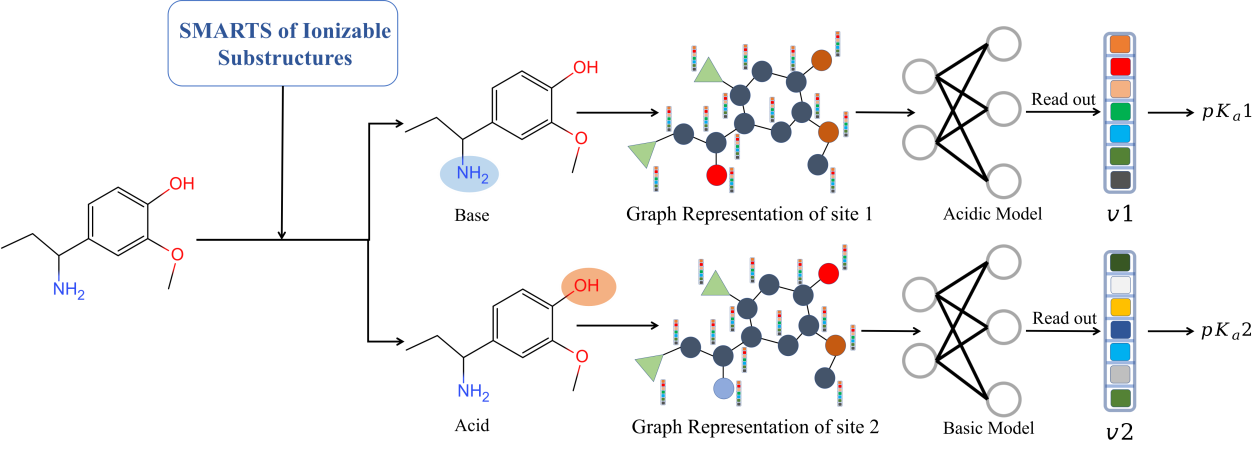
Visual overview of the MolGpka workflow, from the website.
These models have several advantages. They're much faster than QM- or MD-based methods, typically requiring only a small amount of computational work to predict pKa values for an unseen structure. Data-driven methods are also relatively easy to improve—acquiring more experimental data can almost always be used to make the model better in a given domain, making them very useful within the context of a given chemical series or drug-discovery program.
Unfortunately, these models can be unreliable owing to the lack of physical inductive bias. Small chemical perturbations may drive models into less-explored regions of chemical space with less data coverage, resulting in worse predictive accuracy. While training these models on large amounts of data can attenuate these issues, these models are often data-hungry, requiring thousands or tens of thousands of data points to perform well.
Applications:
- Schrödinger's Epik model
- Rowan's Starling macroscopic-pKa model (based on the Uni-pKa architecture)
- MolGpka, a graph-neural-network-based microscopic pKa model
Representative Publications:
- This paper from Xiaolin Pan and co-workers explains how MolGpka works.
- The Uni-pKa paper from DP Technologies explains their energy-based macroscopic pKa architecture, which we adapted into Rowan's macroscopic pKa workflow.
- Jonathan Zheng, Ivo Leito, and William Green outlined the failure of many graph-based pKa methods to properly handle complex protonation equilibria. (Fortunately, energy-based methods like Uni-pKa and Starling don't suffer from this problem.)
- Meital Bojan, Sanketh Vedula, and co-workers used neural network potentials (NNPs) to train a protein pKa model based on the NNP's local representations.
5. Hybrid Approaches
Some methods combine physics-based features with downstream machine learning to create a hybrid model with characteristics of both approaches. Ideally, physics-based descriptors can add a physical inductive bias to the machine-learning model to improve the model's generality and robustness, while maintaining the ability of data-driven models to improve based on additional data. Unfortunately, these models are also reliant on the correctness of the underlying physical assumptions, so errors in the underlying model can propagate into the final predictions. (Plus, physics-based features often make inference slower than a purely data-driven approach.)
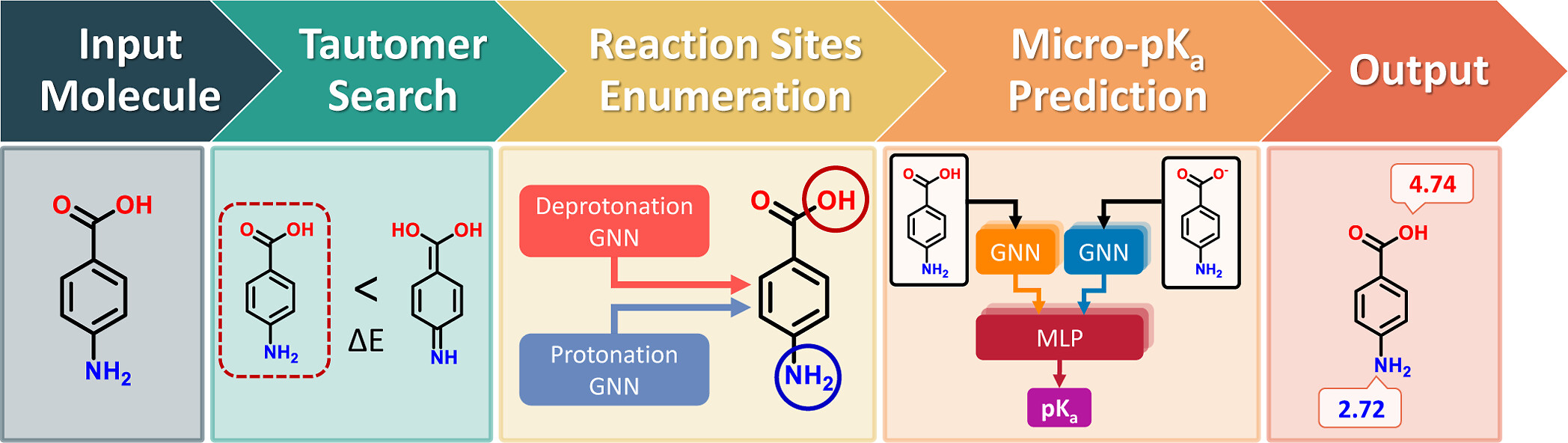
Visual overview of the QupKake workflow, from the original publication.
Applications:
- ChemAxon's pKa plugin (which seems to use charge-based descriptors, although details are sparse)
- The open-source QupKake model (vide supra)
Representative Publications:
- Omri Abarbanel and Geoffrey Hutchison's paper describes how QupKake integrates semiempirical quantum mechanics and machine learning to improve microscopic pKa predictions.
Which Approach Should I Use?
There are no perfect answers in pKa prediction: every scientific problem is different, and it's often useful to benchmark a few different approaches and see what gives the best performance on your systems. Still, we've worked on this problem enough to come up with a few useful heuristics (informed by previous blind pKa-prediction challenges like SAMPL6 and SAMPL7).
The biggest choice in pKa prediction is whether to choose a predominantly data-driven method or a physics-based method. If the structures under study contain "normal" functional groups like those well-represented in pKa databases, or if you need extremely high throughput (like in a virtual-screening campaign), then you're usually best off with a machine-learning model or something similar. These methods are fast and reliable for typical drug-like molecules and have typically been extensively tested for these use cases.
In contrast, if you're dealing with exotic functional groups or complex chemical effects for a small number of systems, then a quantum-chemical method is probably best. These methods are minimally parameterized to experimental data and instead rely on an underlying simulation engine (like DFT or an NNP), making them more resilient and less brittle for unusual species. The downside is that they are considerably slower, making them ill-suited for high-throughput work.
For cases in which solvent or environment effects are expected to predominate (like different protein sidechains), explicit-solvent free-energy methods are almost certainly the right choice, although these calculations typically require considerable domain expertise to run and analyze.