Using Implicit Solvent With Neural Network Potentials
by Corin Wagen · Oct 7, 2025
Neural network potentials (NNPs) are typically trained to reproduce the results of gas-phase density-functional-theory calculations. Unfortunately, chemistry is weird in the gas phase and many reactions don't really exist on the gas-phase potential-energy surface, making it tough to use NNPs to study many important chemical processes.
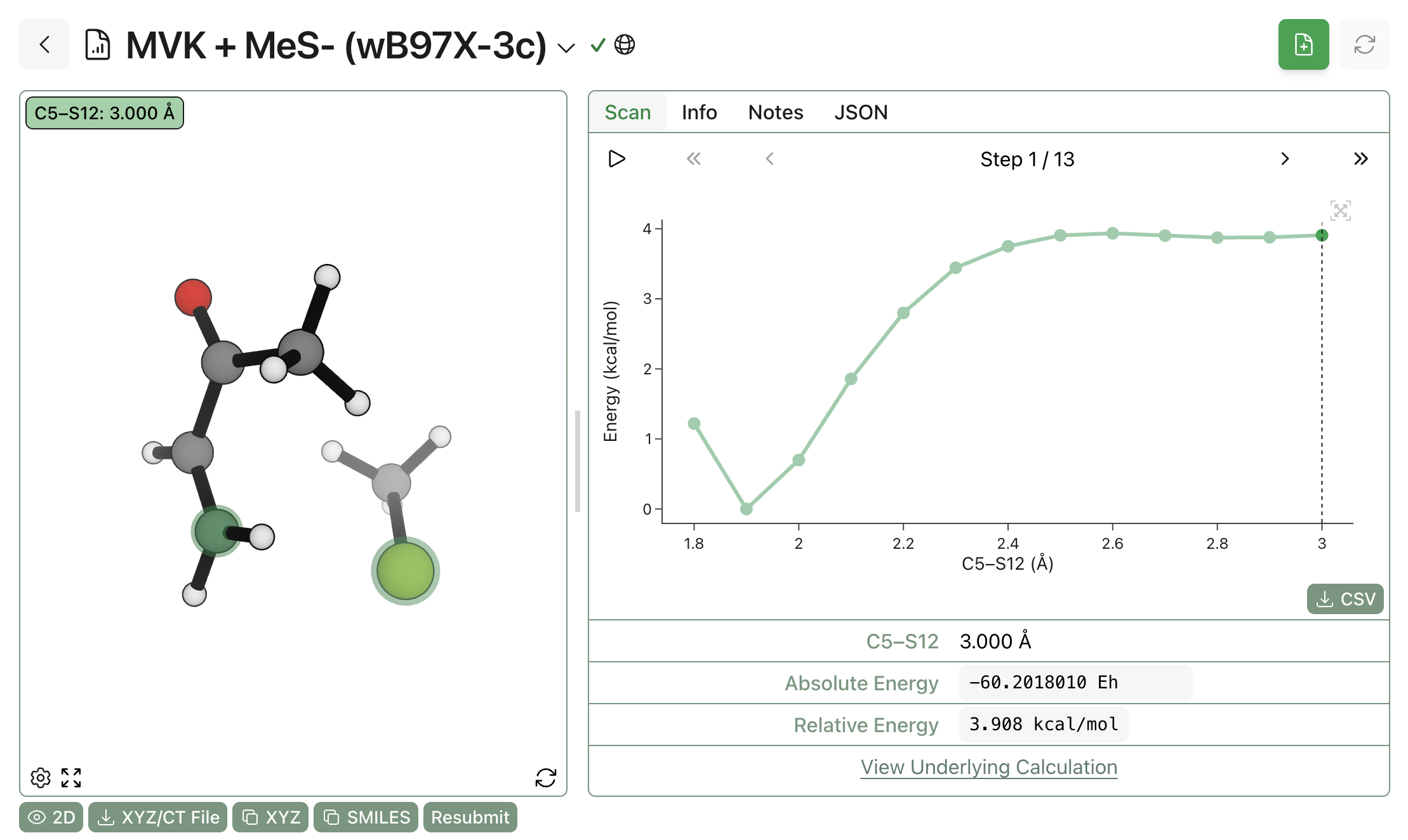
For instance, here's a fairly iconic reaction: the addition of methanethiolate to methyl vinyl ketone. These sorts of thia-Michael additions are fairly common in covalent inhibitors, and we might hope that a simple ground-state two-electron process would be well-described by conventional computational methods. Unfortunately, running a scan for this process in the gas phase shows a confused potential-energy surface without a particularly obvious barrier to thiolate addition.
The fundamental problem is not with the specific computational method but with the fact that this modeling is done in the gas phase: the unsolvated anions are so unstable and reactive that this addition becomes almost barrierless. Without the ability to add solvent corrections, even the best NNP will be incapable of usefully modeling this chemistry.
One solution to this problem is to train a separate NNP on implicit-solvent DFT calculations. This has been done before—Roman Zubatyuk and co-workers used transfer learning to build a version of AIMNet that predicted energies with implicit water—but necessitates training a new model for every solvent under study, which isn't ideal.
Instead, we've built machinery here at Rowan to separately compute the energy of solvation using semiempirical quantum chemistry. Using the analytical linearized Poisson–Boltzmann (ALPB) implicit-solvent model in combination with Grimme's GFN2-xTB semiempirical method, we're able to quickly add solvent corrections to calculations from any NNP. While this makes calculations slightly slower (since we have to run xTB calculations in addition to standard NNP calculations), the results are much improved for many reactive systems.
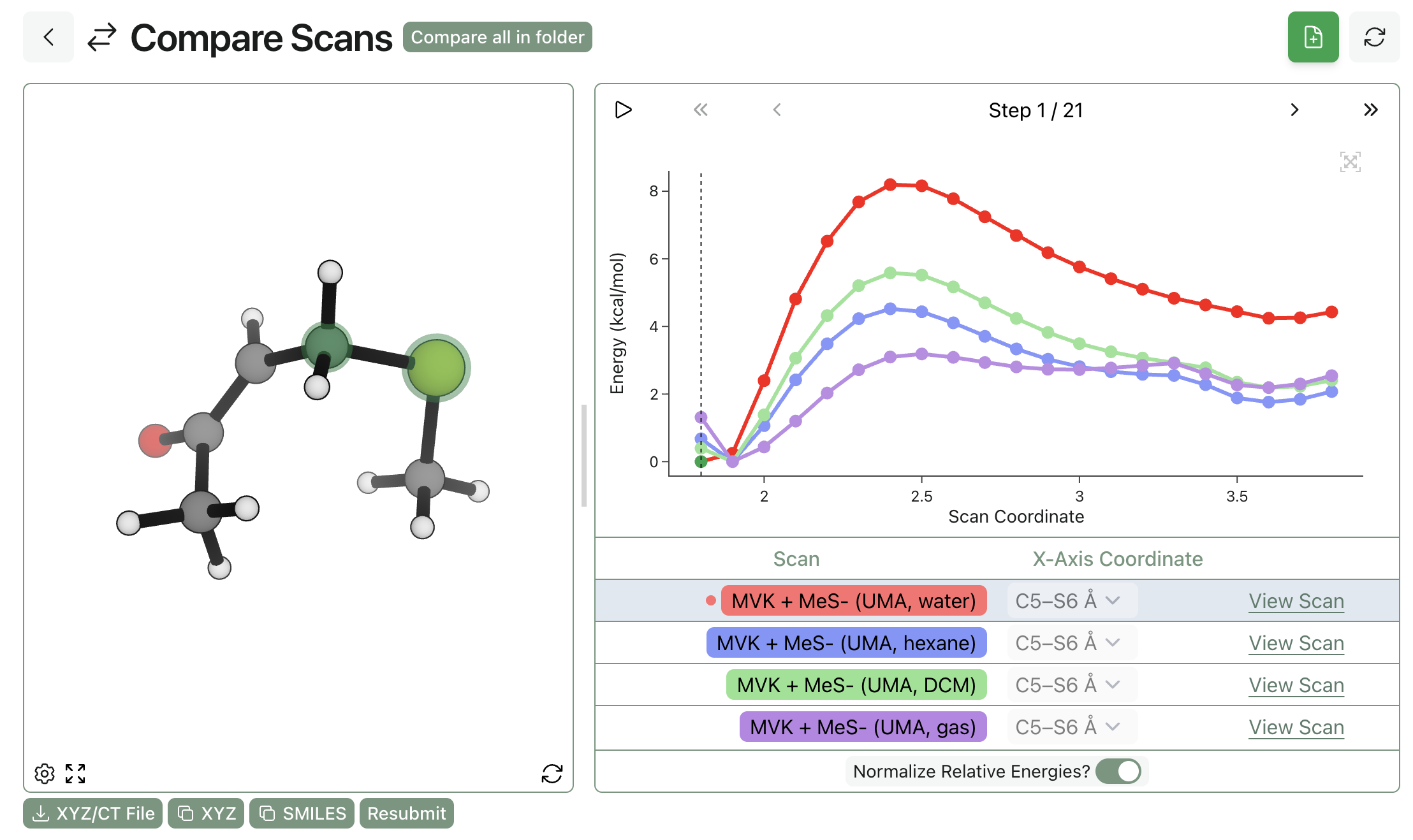
Here's the same thia-Michael addition with ALPB solvation. As the strength of the solvent increases from gas-phase (purple) to hexane (blue) to dichloromethane (green) to water (red), we can see that the barrier becomes more defined and the reaction becomes more clearly downhill, as expected.
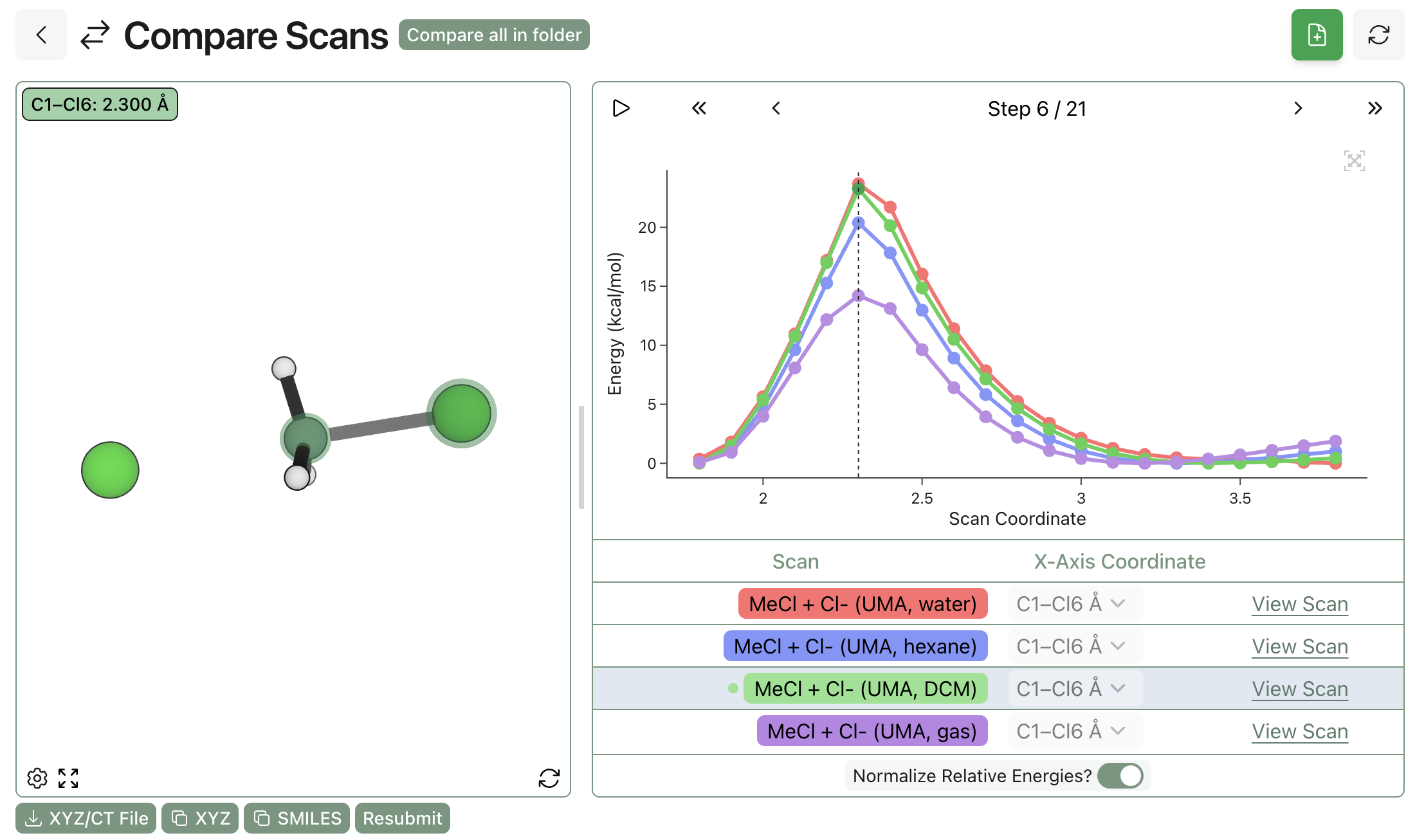
Adding implicit solvent to NNPs can also be useful even in cases where the underlying PES is described qualitatively correctly in the gas phase. The prototypical SN2 reaction between chloride and methyl chloride has a low barrier of around 14 kcal/mol, but addition of an implicit-solvent water model produces a more reasonable barrier of about 23 kcal/mol. (Note that these barriers are estimated from the scan graph, and that actual thermochemical calculations should be performed to get quantitative barrier-height estimates.)
A few caveats are worth noting here. This approach relies on GFN2-xTB/ALPB getting the underlying chemistry approximately correct, and so it might not work in every case. Also, the requisite xTB calculations require matrix diagonalization and thus can become slow for large systems—this isn't as scalable as a pure NNP-based approach. Still, we've found that the ALPB-based approach is quite effective and allows us to model a lot of properties and reactions with much-improved accuracy.
If you want to try combining NNPs with ALPB yourself, it's very simple to do through Rowan. Simply select any NNP from Rowan and then choose ALPB from the solvent menu:
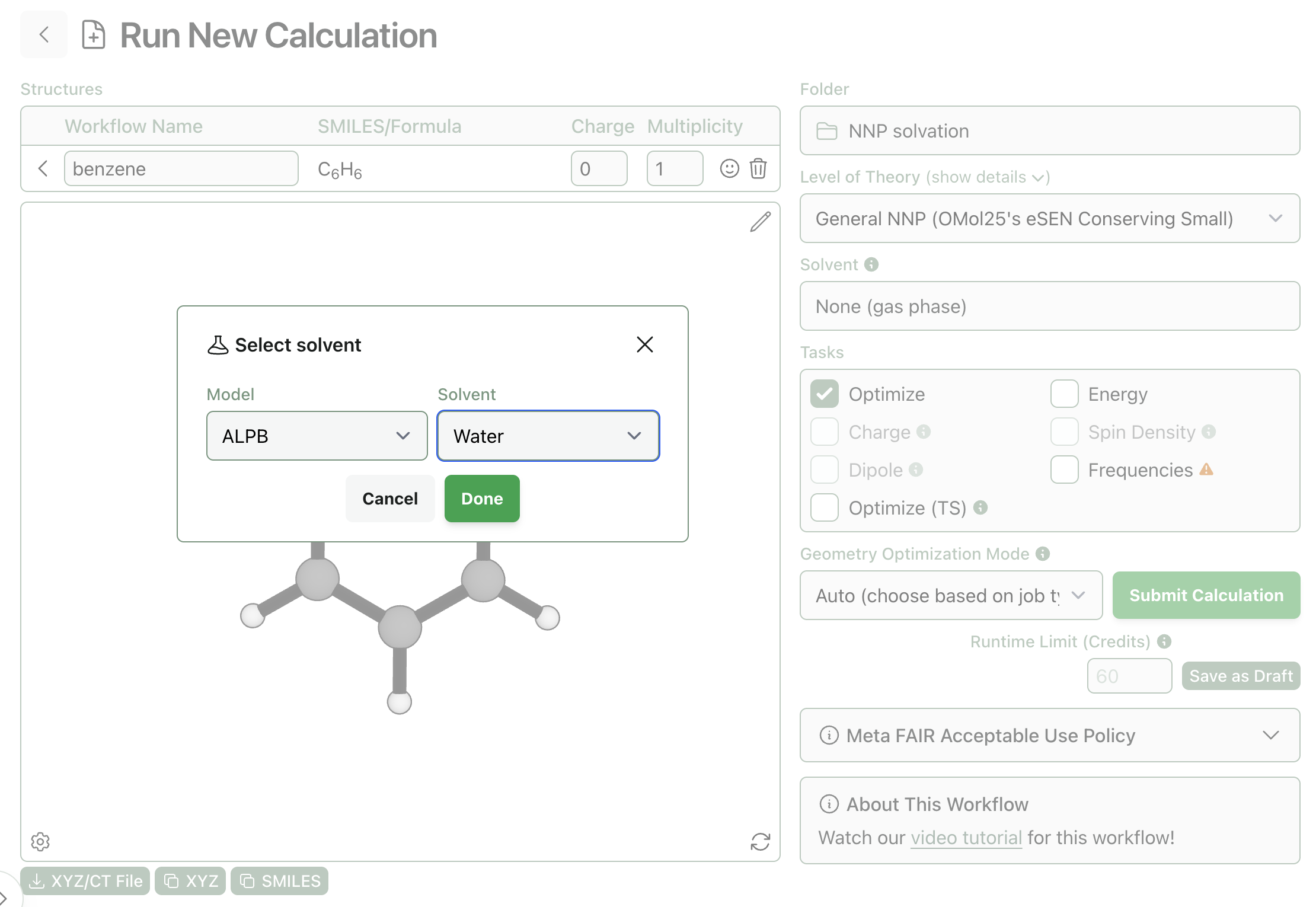
How to add ALPB to an NNP in Rowan.
That's it! We automatically take care of adding implicit-solvent corrections for geometry optimization, single-point energies, and frequency calculations. If this is of interest to your research, you can try this out for free today by making a Rowan account.