Which Optimizer Should You Use With NNPs?
by Ari Wagen and Corin Wagen · Sep 4, 2025
Update, September 5, 2025: We've updated this post to include results from Sella using internal coordinates, which we refer to as "Sella (internal)" in the Results tables. Our reflections on these new data are in the Updates section below.
On August 27th, Orbital Materials released their latest open-source model, "OrbMol." OrbMol combines Orbital's super-scalable Orb-v3 neural network potential (NNP) architecture with Meta et al.'s massive Open Molecules 2025 (OMol25) dataset (which we've written about previously).
To the best of my knowledge, this is the first NNP trained on the full OMol25 dataset from outside the OMol25 team. This is a huge accomplishment for Orbital Materials and impressively fast too—we can only imagine how many GPUs were involved in the creation of OrbMol!
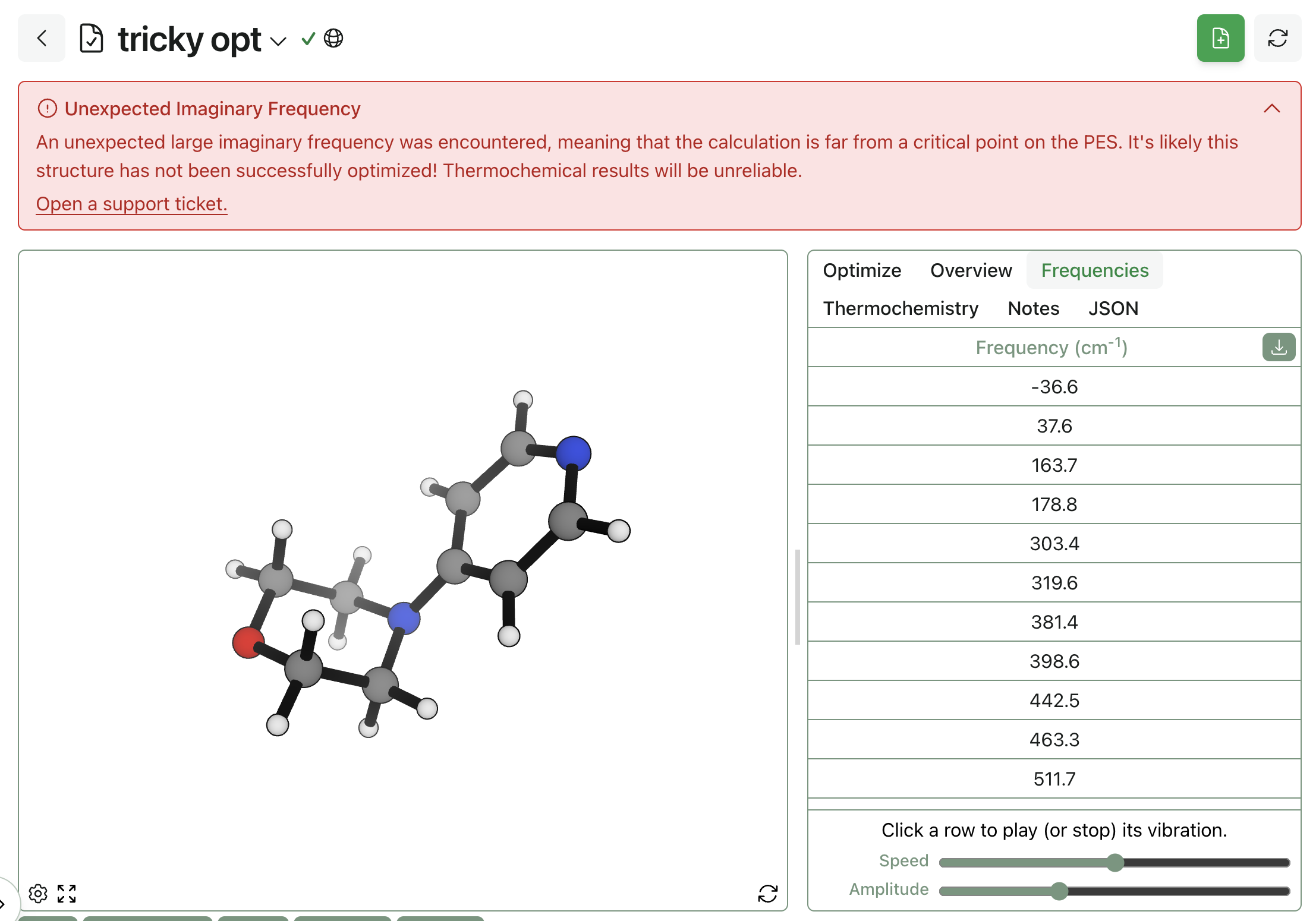
After running OrbMol through our internal benchmark suite at benchmarks.rowansci.com, one result stuck out as anomalous: OrbMol matches the performance of the UMA and eSEN models trained on OMol25 for single-point-energy-derived tasks, but it failed to complete optimizations of 25 drug-like molecules using the Sella optimizer with 0.01 eV/Å fmax and max. 250 steps.
When I (Ari) shared these results on X, many people commented asking about our choice of Sella. In this blog post, we'll discuss how we conceived of this simple optimization test—what it's good for and what it leaves unanswered—and study the effect of optimizer on these results by comparing each combination of four optimizers (Sella, geomeTRIC, and ASE's implementations of FIRE and L-BFGS) and four NNPs (OrbMol, OMol25's eSEN Conserving Small, AIMNet2, and Egret-1) with GFN2-xTB serving as a "control" low-cost method.
Why Report Successful Optimization Counts at All?
At Rowan and in our conversations with industry scientists, we've found that the most common use case for NNPs is as a drop-in replacement for density–functional-theory (DFT) calculations. Optimizing a molecule with DFT is often the most time-consuming and compute-intensive step in many standard modeling workflows. NNPs can offer real value in the short term, but only if they can reliably replace DFT for these routine optimization tasks.
Most common benchmarks that people use for benchmarking quantum-chemical methods, semiempirical methods, and NNPs measure a method's ability to recreate energies at specific points on the potential energy surface. Many of these energy vs. energy benchmarks are quite nuanced and insightful, like GMTKN55, which accumulates results across 55 different subsets of relative energy challenges, or Wiggle150, which measures a method's ability to rank order highly-strained conformers of three drug-like molecules. However, these energy-based benchmarks fail to conclusively prove that NNPs can reliably serve as replacements for DFT in the context of molecular optimization.
To attempt to fill this gap, we chose 25 drug-like molecules to compare each NNP along the following axes:
- How many molecular optimizations finish? We limit each run to 250 optimization steps, and call it converged once the maximum atomic force drops below 0.01 eV/Å (0.231 kcal/mol/Å).
- What's the average number of steps that optimizations take to complete?
- How many optimized structures are true local minima? In other words, how many optimized structures have 0 imaginary frequencies?
- What's the average order of the equilibria structure reached? In other words, what's the average number of imaginary frequencies per optimized structure?
These tests matter because practitioners use DFT to optimize starting structures with the goal of finding true local minima as quickly as possible. An NNP that aims to replace DFT must not only reproduce conformer rankings and relative energies, but also reliably complete optimizations in few steps without yielding imaginary frequencies.
The 25 molecular structures under study are available on GitHub.
Optimizer x NNP Study
We chose four common optimization methods for this benchmark study.
1. L-BFGS
The limited-memory Broyden–Fletcher–Goldfarb–Shanno algorithm (L-BFGS) is a classic quasi-Newton algorithm used in all sorts of contexts. Like all second-order methods, L-BFGS can get confused by noisy potential-energy surfaces. In this study, we use the L-BFGS optimizer implemented in the Atomic Simulation Environment.
2. FIRE
The fast inertial relaxation engine (FIRE) is a first-order minimization method designed for fast structural relaxation. FIRE uses a molecular-dynamics-based approach, making it faster and more noise-tolerant than Hessian-based methods like L-BFGS. However, it's also a bit less precise and often performs worse for complex molecular systems. In this study, we used the FIRE optimizer implemented in the Atomic Simulation Environment.
3. Sella
Sella is an open-source package developed by the Zador lab at Sandia National Laboratories. While Sella is often used for transition-state optimization, it also implements rational function optimization to optimize structures towards minima. Sella uses an internal coordinate system alongside a trust-step restriction and a quasi-Newton Hessian update.
4. geomeTRIC
geomeTRIC is a general-purpose optimization library developed by the Wang lab at UCSD. geomeTRIC uses a special internal coordinate scheme called "translation–rotation internal coordinates" (TRIC); within this coordinate system, it uses standard L-BFGS with line search. For this study, geomeTRIC was used with both Cartesian ("cart") and TRIC ("tric") coordinates.
These choices represent common "good" optimizers used by the community; a recent benchmark from Akhil Shajan and co-workers found Sella to be the best open-source geometry optimizer when using HF/6-31G(d,p) gradients on the Baker test set, although geomeTRIC also did quite well.
Convergence Criteria
Most optimization and quantum chemistry libraries give users detailed control over optimization criteria. For instance, geomeTRIC determines if a structure is optimized based on five criteria:
- The change in energy from the previous step
- The maximum component of the gradient vector
- The RMS of the gradient vector
- The maximum component of the displacement vector
- The RMS of the displacement vector
These criteria are used by Gaussian, NWChem, TurboMole, TeraChem, Q-Chem, ORCA, and so on. Unfortunately, ASE's interface for optimizers only exposes fmax, the maximum component of the gradient vector. (This is one of the reasons we currently use geomeTRIC at Rowan; we want to make sure that "optimized" structures are fully optimized.)
To enable a fair comparison with ASE optimizers, convergence was determined solely on the basis of the maximum gradient component for this study. All other convergence criteria were disabled in geomeTRIC. (We're aware that this is suboptimal, and discuss this more in our "Limitations" section.)
Results
For brevity, OMol25's eSEN Conserving Small is referred to simply as "OMol25 eSEN" in the below tables.
Number Successfully Optimized
This metric reports how many of the 25 systems the given NNP-optimized pairing was able to successfully optimize.
| Optimizer \ Method | OrbMol | OMol25 eSEN | AIMNet2 | Egret-1 | GFN2-xTB |
|---|---|---|---|---|---|
| ASE/L-BFGS | 22a | 23 | 25 | 23 | 24 |
| ASE/FIRE | 20 | 20 | 25 | 20 | 15 |
| Sella | 15 | 24 | 25 | 15 | 25 |
| Sella (internal) | 20 | 25 | 25 | 22 | 25 |
| geomeTRIC (cart) | 8 | 12 | 25 | 7 | 9 |
| geomeTRIC (tric) | 1 | 20 | 14 | 1 | 25 |
aBenjamin Rhodes reports that OrbMol succesfully optimizes all 25 systems when using "float32-highest" precision and L-BFGS with max. 500 steps.
All of the unsuccessful optimizations failed because they exceeded 250 optimization steps, with a single exception: the Sella optimization of brexpiprazole with OMol25's eSEN Conserving Small failed with a nondescript "Internal Error."
Average Number of Steps
This metric tells us the average number of steps needed for successful optimizations.
| Optimizer \ Method | OrbMol | OMol25 eSEN | AIMNet2 | Egret-1 | GFN2-xTB |
|---|---|---|---|---|---|
| ASE/L-BFGS | 108.8 | 99.9 | 1.2 | 112.2 | 120.0 |
| ASE/FIRE | 109.4 | 105.0 | 1.5 | 112.6 | 159.3 |
| Sella | 73.1 | 106.5 | 12.9 | 87.1 | 108.0 |
| Sella (internal) | 23.3 | 14.88 | 1.2 | 16.0 | 13.8 |
| geomeTRIC (cart) | 182.1 | 158.7 | 13.6 | 175.9 | 195.6 |
| geomeTRIC (tric) | 11 | 114.1 | 49.7 | 13 | 103.5 |
Number of Minima Found
This metric tells us how many of the 25 systems optimized to a local minimum (as opposed to saddle points). This is determined via a frequencies calculation; the presence of an imaginary frequency indicates that a local minima was not found.
| Optimizer \ Method | OrbMol | OMol25 eSEN | AIMNet2 | Egret-1 | GFN2-xTB |
|---|---|---|---|---|---|
| ASE/L-BFGS | 16 | 16 | 21 | 18 | 20 |
| ASE/FIRE | 15 | 14 | 21 | 11 | 12 |
| Sella | 11 | 17 | 21 | 8 | 17 |
| Sella (internal) | 15 | 24 | 21 | 17 | 23 |
| geomeTRIC (cart) | 6 | 8 | 22 | 5 | 7 |
| geomeTRIC (tric) | 1 | 17 | 13 | 1 | 23 |
Average Number of Imaginary Frequencies
This metric tells us how many imaginary frequencies each successfully optimized structure had on average.
| Optimizer \ Method | OrbMol | OMol25 eSEN | AIMNet2 | Egret-1 | GFN2-xTB |
|---|---|---|---|---|---|
| ASE/L-BFGS | 0.27 | 0.35 | 0.16 | 0.26 | 0.21 |
| ASE/FIRE | 0.35 | 0.30 | 0.16 | 0.45 | 0.20 |
| Sella | 0.40 | 0.33 | 0.16 | 0.47 | 0.36 |
| Sella (internal) | 0.3 | 0.04 | 0.16 | 0.23 | 0.08 |
| geomeTRIC (cart) | 0.38 | 0.33 | 0.12 | 0.29 | 0.22 |
| geomeTRIC (tric) | 0.00 | 0.15 | 0.07 | 0.00 | 0.08 |
Limitations
This is a blog post, not a full study, and there are plenty of limitations here. A few obvious ones:
- We're not assessing the accuracy of potential-energy surfaces at all here. It's entirely possible that the location and the depth of these minima are totally incorrect—this can be assessed with other benchmarks, but we haven't done so here.
- These structures are far from a representative sample of chemical space—we chose only common drug-like molecules and didn't include any metals, non-covalent complexes, or anything with exotic functionality.
- We haven't tuned hyperparameters at all—it's likely that considerable improvements are possible for all methods here. In particular, the surprisingly bad performance of geomeTRIC with TRIC internal coordinates suggests that something's going wrong; one possibility is that zeroing out most of geomeTRIC's convergence criteria leads to pathological behavior.
- Relatedly, this study looks at a lot of different factors at once. Different methods might have different default hyperparameters, different initial Hessian guesses (for second-order methods), and any other number of relevant implementation details. Our work is intended as a pragmatic "guide to the perplexed" aimed at people trying to use these packages to run calculations, not a comprehensive study on how to develop the best optimizer.
- The surprisingly high success of AIMNet2 might point to the benefit of explicit long-range forces, but it also might just mean that the starting structures were closer to minima for AIMNet2. Since each NNP has its own potential-energy surface, making fair comparisons between them is difficult.
- As discussed above, the convergence criteria we used are suboptimal—it's possible that these structures aren't fully minimized according to other criteria (or a lower
fmax). Future benchmarks should assess the performance of methods like FIRE and L-BFGS using state-of-the-art convergence criteria that more closely mimic accepted best practices. - And we've only looked at simple unconstrained optimizations here, not transition-state optimizations or optimizations with constraints.
There's so much more work to do here! We hope that our work motivates further research, and we plan to investigate this more ourselves.
Takeaways
Still, we think we have enough data to draw a few tentative conclusions.
1. Better Benchmarks Are Needed
A 2022 paper from Xiang Fu and co-workers stated that "forces are not enough" for benchmarking NNPs. Fu showed that even NNPs with good error metrics for energy and forces could give unrealistic and unstable MD simulations, pushing the field to more aggressively benchmark MD stability with new NNPs (like eSEN, which was specifically designed to give smooth potential-energy surfaces).
Just as Fu showed that "the ability to run stable MD simulations" was an important benchmark for NNPs, we think that "the ability to optimize to true minima on the PES" should also be used for benchmarking future NNPs.
2. The Optimization Method and Coordinate System Matter
Different optimization methods performed very differently, even for the same NNP. In our experience, most scientists spend considerably more time benchmarking the level of theory than the optimizer they use. At least for NNPs, our results suggest that finding the right optimizer for a given class of systems might be just as crucial as finding the right method. If you're going to run hundreds or thousands of optimizations, it might be worth benchmarking optimizers or tuning hyperparameters before running everything.
3. NNPs Might Need New Optimizers
Second-order optimizers like L-BFGS make certain assumptions about the smoothness of the potential-energy surface that might not be true for all NNPs. A recent study from Filippo Bigi and co-workers shows that non-conservative NNPs perform worse on geometry-optimization benchmarks, particularly for second-order optimizers; we anticipate that other NNP architectural decisions will have similar impacts on optimization performance.
While MD-based optimizers like FIRE are allegedly better in contexts like this, since they make fewer assumptions about the nature of the potential-energy surface, our results show that FIRE is not significantly better on this benchmark.
We'd like to see more work on building noise-tolerant optimizers for NNPs. Papers like this work from Bastian Schaefer and co-workers suggest that it's possible to improve classic L-BFGS methods for noisy cases, but to our knowledge there aren't good implementations of this work or related methods for molecular geometry optimization. New optimization methods could help scientists better leverage advances in NNPs and conduct high-throughput calculations much more efficiently. If you're interested in working on this, please reach out to our team! We'd like to talk.
So, with all this in mind, let's try to answer the question in the title—if you're running optimizations with NNPs today, which optimizer should you use? Our results suggest that the ASE L-BFGS is the best plug-and-play choice right now—for almost every NNP, L-BFGS converges more structures, and L-BFGS structures have fewer imaginary frequencies. While there are plenty of reasons why you might choose a different optimizer (convergence control, constraints, and so on), we think that L-BFGS is an excellent "first choice" for routine work.
Updates
Friday, September 5, 2025. The Sella optimizer has weird defaults. For one, it defaults to running transition state optimizations; to instead optimize towards local minima, you have to explicitly pass order=0. For another, Sella defaults to using Cartesian coordinates; to switch to internal coordinates, you have to explictly pass internal=True.
Our original tests were run using order=0 and no internal keyword argument, meaning Sella defaulted to running optimizations in Cartesian space. When running our test with Sella using internal coordinates, each optimization step took longer, but the overall optimization converged in far fewer steps. (We hope to do a more thorough wallclock-time-based optimizer study in the future.)
Looking at the results, we're impressed: using internal coordinates, Sella converged as many systems as ASE/L-BFGS, found more true minima than ASE/L-BFGS, and did so in fewer steps.
While ASE/L-BFGS remains a good optimizer choice, we think these new data suggest that Sella (with internal coordinates) is a better plug-and-play optimizer for use with NNPs. (And we're excited to continue studying this!)