Rowan

Egret-1: Pretrained Neural Network Potentials for Efficient and Accurate Bioorganic Simulation

Elias L. Mann, Corin C. Wagen, Jonathon E. Vandezande, Arien M. Wagen, Spencer C. Schneider
Apr 30, 2025
Accurate simulation of atomic systems has the potential to revolutionize the design of molecules and materials. Unfortunately, exact solutions of the Schrödinger equation scale as O(N!) and remain inaccessible for systems with more than a handful of atoms, forcing scientists to accept steep tradeoffs between speed and accuracy and limiting the reliability and utility of the resultant simulations. Recent work in machine learning has demonstrated that neural network potentials (NNPs) can learn efficient approximations to quantum mechanics and resolve this tradeoff, but existing NNPs still suffer from limited accuracy relative to state-of-the-art quantum-chemical methods. Here, we present Egret-1, a family of large pre-trained NNPs based on the MACE architecture with general applicability to main-group, organic, and biomolecular chemistry. We find that the Egret-1 models equal or exceed the accuracy of routinely employed quantum-chemical methods on a variety of standard tasks, including torsional scans, conformer ranking, and geometry optimization, while offering multiple-order-of-magnitude speedups relative to legacy methods. We also highlight important lacunae for future NNP research to investigate, and suggest strategies for building future high-quality models with increased scale and generality.

This preprint can also be viewed on arXiv. The models are available on GitHub.

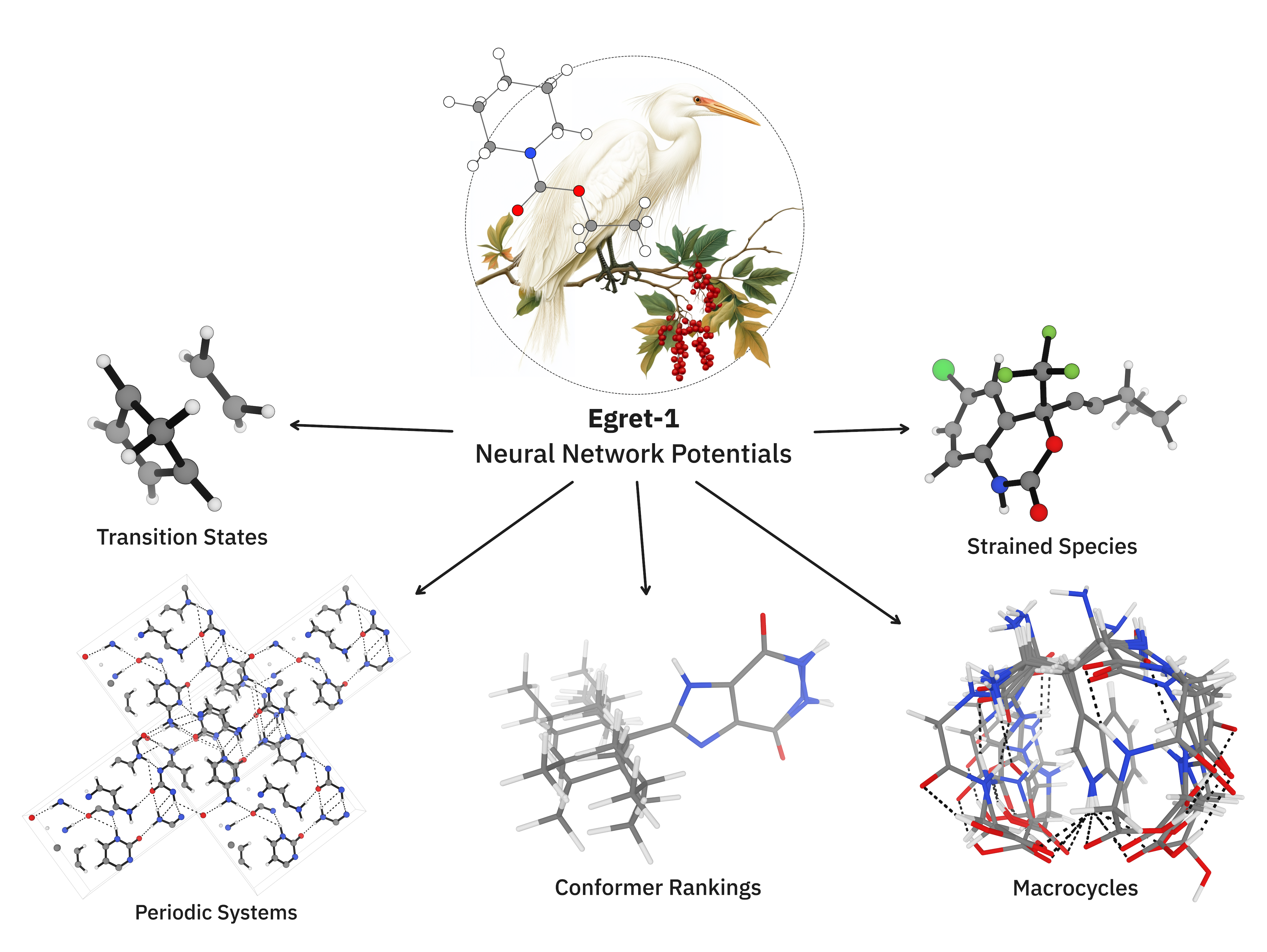
Visual abstract showcasing Egret-1's capabilites in bioorganic simulation

Introduction

Rational simulation-guided design of atomic systems has been a dream of researchers across the chemical sciences for decades. In principle, fast, accurate, and reliable simulation could lead to vast research accelerations by allowing scientists to replace costly laboratory experiments with fast and inexpensive calculations. High-accuracy prediction of protein–ligand binding affinities would accelerate hit-to-lead optimization in drug discovery and allow limited experimental resources to be allocated more efficiently, while simulation of crystal polymorph landscapes could prevent polymorphism-driven process catastrophes like Abbott's 1998 ritonavir withdrawal.1–3 In materials science, prediction of material properties could vastly accelerate the search for new polymers, batteries, and carbon-capture materials, and the ability to accurately simulate reaction mechanisms could enable more efficient industrial processes and the design of next-generation catalysts.2

Unfortunately, these "holy grails" for computational chemistry and materials science remain largely the domain of science fiction.2,4 Exact solutions of the Schrödinger equation scale as O(N!)O(N!) and remain inaccessible for systems with more than a handful of atoms,5 requiring scientists today to accept steep tradeoffs between speed and accuracy when conducting simulations. While the immense difficulty and importance of this problem has given rise to a plethora of different research programs over the past century, two main approaches have emerged, each with their own advantages and disadvantages.

The first of these approaches, quantum chemistry, seeks to find efficient physically justified approximations to the Schrödinger equation that enable computations to be completed on real systems while maintaining the accuracy and generality of the underlying theory as much as possible. Over the past century, this field has advanced to the point where many molecular properties can now be predicted with greater-than-experimental accuracy and calculations can routinely be run on systems with hundreds of atoms. Yet these approaches are still too slow and costly to model large systems or dynamic processes,6–8 even though 20–40% of many national supercomputers' time is already spent running quantum chemistry.9

The second of these approaches, molecular mechanics, replaces quantum mechanics-based theories altogether with simple classical models fit to reproduce experimental or quantum mechanics-derived values.10 While these forcefield models allow for many order-of-magnitude speedups relative to quantum chemistry, their limited expressivity makes them unable to describe many complex chemical phenomena. The shortcomings of conventional forcefields have been shown to result in inaccurate predictions of small molecule conformational and torsional preferences, RNA structure, protein-folding dynamics, and hydration free energies.11–17 Furthermore, most forcefields are by design unable to model reactive processes that involve forming or breaking bonds, limiting their applicability to many important chemical phenomena like catalysis and covalent inhibition.

In recent years, machine-learned models of atomic systems have emerged as a potential resolution to this dilemma. Neural network potentials (NNPs) are machine-learned models trained to reproduce high-level quantum-chemical calculations, typically density-functional theory (DFT), which once trained can mimic the results of quantum chemistry with a single forward-inference step. While early NNPs were trained anew for each specific topology under study, modern NNPs have shown the ability to function as general-purpose forcefields for entire regions of chemical space without system-specific retraining.18–22 In some cases, NNPs have also been shown to approach the accuracy of the underlying training data while running many orders-of-magnitude faster.23

Despite the immense promise of NNPs, their ability to drive vast improvements in atomistic simulation is limited by three main factors:

Here, we focus only on the first of these questions, leaving questions of speed and generality to future study. We study the effect of increasing dataset size and diversity for NNPs based on the MACE architecture within the domain of organic and biomolecular chemistry. We also introduce 3 general pretrained models under an MIT license—Egret-1, a general-purpose model for bioorganic simulation; Egret-1e, additionally trained on a variety of main-group structures and superior at thermochemistry; and Egret-1t, additionally trained on transition states—and demonstrate that these models can achieve DFT-level performance for broad regions of chemical space without task-specific fine-tuning, even with conventional datasets and architectures. We highlight the limitations of state-of-the-art NNPs (including the Egret-1 models), and suggest avenues for further improvement.

Methods

Dataset

In an effort to train more generalizable and accurate models, we compiled a variety of datasets and recomputed all structures at the ωB97M-D3BJ/def2-TZVPPD39,40 level of theory to match the original MACE-OFF23 41 dataset. In this work, we studied the following datasets, with the caveat that not the entire dataset was added in every case:

We also generated an additional dataset ("Finch", F) from scratch. We iteratively loaded structures from GDB1749 & COCONUT50 and used COATI51 to generate plausible nearby structures, using agglomerative clustering on the output set to discard similar structures. We generated initial structures for each molecule using the ETKDG52 algorithm and ran 10 ps of metadynamics using GFN2-xTB53 with a 1 fs timestep. (The mass of the hydrogen atoms was kept as 1 amu, and the default SHAKE constraints were disabled.) From each output trajectory, 20 dissimilar conformations were selected by agglomerative clustering on heavy-atom RMSD and added to the dataset. (For a subset of the molecules, extra solvent molecules or additives were added to generate complexes of up to four molecules.) We note that metadynamics has previously been proposed as an efficient way to generate training data for NNPs.54

For training, we excluded all non-neutral structures and all structures containing a force magnitude greater than 1 Hartree/Å.

We studied many combinations of datasets (vide infra), and ultimately selected three for the final Egret-1 models:

Model Architecture

The Egret-1 models are derived from the MACE architecture, a high-body-order equivariant message-passing neural network (MPNN) architecture.55,56 Here we provide a brief explanation of the architecture; for more details, please refer to the original publication.56

Graph neural networks are inherently permutation invariant, meaning the model's output depends only on the structure of the graph, not on the order in which the atoms and their features are presented. (More generally, a model is invariant to a transformation if applying that transformation to the input of the model does not change the output: f(G)=f(TG)f(G) = f(\cal T G).) Permutation invariance is important for predicting the potential energy of a molecule, since it is dependent on the structural relationships between atoms, not their order.

MACE models are designed to be SO(3) (special orthogonal group in 3 dimensions) equivariant, meaning that any rotation in 3D space to the input of the model will rotate the output the same way: f(QG)=Qf(G)f(Q G) = Q f(G). (More generally, a model is equivariant to a given transformation if the output of the model transforms predictably when said transformation is applied to the input of a model: f(TG)=T′f(G)f(\cal T G) = \cal T ^\prime f(G).) SO(3) equivariance is important for accurately predicting directional vectors like atom-centered forces.

The body order of an MPNN refers to the number of nodes jointly considered when constructing a message to update the hidden state of a node in a graph. A body order of 2 means that messages are based on pairwise interactions between the central node and each of its neighbors, typically depending only on radial distances. A body order of 3 extends this to include triplet interactions, involving angles formed between the central node and pairs of its neighbors. Increasing the body order allows the MPNN to capture more complex geometric relationships, making the model more expressive, but it also substantially increases the computational cost.

MACE reduces the complexity of computing high-body-order interactions by constructing them from the outer product of all two-body messages. Any regular, local function of the atomic environment can be represented within the span of this outer-product basis, including higher-order relationships between nodes. This approach avoids explicitly computing high-dimensional sums over all body-order combinations. For full proof and derivation, see Ref. 56.

MACE extends the atomic cluster expansion (ACE) formulation that any smooth, permutation-invariant and rotation-equivariant function of atomic position can be represented to arbitrary precision as an expansion over body-ordered clusters of atoms.57 This is used to represent the potential energy of a molecule:

Ei=∑Knlcnl(K)Binl(K)E_i = \sum_{K n l} c^{(K)}_{n l} B^{(K)}_{i n l}

Etotal=∑iEiE_\text{total} = \sum_i E_i

where EiE_i is the energy contribution of atom ii, KK is the body order, nn is the radial-basis index and ll is the angular degree (spherical-harmonic degree). Binl(K)B^{(K)}_{i n l} are the body-ordered basis functions, and cnl(K)c^{(K)}_{n l} are the learned coefficients.

As body order increases and the resolution of the radial and angular bases improves (determining the precision at which distances and angles are represented), the potential energy function can be approximated to arbitrary accuracy. MACE constructs the atomic cluster expansion as

Ei=(∑t=0T−1∑k~Wreadout,k~(t)hi,k~00(t))+MLPreadout(T)({hik00(T)}k)E_i = (\sum^{T-1}_{t=0} \sum_{\tilde{k}} W^{(t)}_{\text{readout}, \tilde{k}} h^{(t)}_{i, \tilde{k}0 0}) + \text{MLP}^{(T)}_{\text{readout}} (\{h^{(T)}_{i k 0 0}\}_k)


where the term ∑k~Wreadout,k~(t)hi,k~00(t)\sum_{\tilde{k}} W^{(t)}_{\text{readout}, \tilde{k}} h^{(t)}_{i, \tilde{k}0 0} is analogous to the cnl(K)Binl(K)c^{(K)}_{n l} B^{(K)}_{i n l} expansion in ACE: a linear combination of all channels k~\tilde{k} in the invariant subspace of the hidden state hh for atom ii at message-passing layer tt. Here, ll and mm denote the degree and order of the spherical harmonics, both equal to 0 for invariant terms. Summing the readouts across message-passing layers is analogous to summing over increasing body orders in ACE. An additional multi-layer perceptron (MLP) applied to the final hidden state at layer TT serves as a nonlinear correction to capture higher-body-order contributions that are not explicitly computed.

Model Training

Models were trained using PyTorch Lightning,58 Hydra configuration management,59 and Distributed Data Parallel for multi-GPU training. We adopted hyperparameters nearly identical to those reported for MACE-OFF23(L), with the exception of removing early stopping and increasing the cutoff radius from 5Å to 6Å.41 Training was conducted on a cluster of 4 NVIDIA H100 GPUs: Egret-1 required 85 hours to train, Egret-1t required 91 hours, and Egret-1e took 105 hours.

Consistent with the original MACE-OFF23 training strategy, we employed exponential moving average (EMA) of model weight updates throughout training. Each model was trained for 190 epochs, and the loss function combines linearly weighted contributions from both energy and force predictions. For the first 115 epochs, we applied a force loss weight wforces=1000w_{\text{forces}} = 1000 and an energy loss weight wenergy=40w_{\text{energy}} = 40. During the remaining 65 epochs, stochastic weight averaging (SWA) was used, and the loss weights were adjusted to wforcesSWA=10w^{\text{SWA}}_{\text{forces}} = 10 and wenergySWA=1000w^{\text{SWA}}_{\text{energy}} = 1000. This training schedule mirrors that of MACE-OFF23 prioritizing force learning during the early phase and shifting focus toward energy accuracy during the averaging phase.41

For a full list of hyperparameters, see Table 15 and Table 16 in the Appendix.

To split the dataset into train and validation sets, we grouped structures by molecule to avoid validation-set leakage. Structures were compared by generating a Weisfeiler–Lehman60 graph hash with NetworkX.61 Molecules with identical hashes were treated as conformers of the same molecule. To preserve dataset stratification, all structures corresponding to a given molecule were assigned to the same subset. If a molecule appeared in more than one subset, the molecule was assigned to the subset with fewer structures. Subsets were pooled prior to the train-validation split to avoid inter-subset data leakage. For each subset, 80% of the molecules were assigned to the training set and 20% to the validation set. We then computed the ratio for our train–validation split based on the number of structures to ensure a reliable split; in all cases, the ratio was within 1% of the desired 80/20 train/validation split.

Benchmarking

We evaluate the Egret-1 models against a compendium of theoretical methods commonly used in atomistic simulations, broadly categorized to the unfamiliar reader as follows:

To more specifically assess the performance of Egret-1 relative to existing NNPs, we benchmark against a set of three high-quality reference models:

All density-functional-theory computations were conducted with Psi4 1.9.1.68 For benchmarking, the default settings in Psi4 were modified somewhat: a (99,590) integration grid with "robust" pruning, the Stratmann–Scuseria–Frisch quadrature scheme was employed,69 and an integral tolerance of 10−1410^{-14} was used throughout. Density fitting was employed for all calculations, and a level shift of 0.100.10 Hartree was applied to accelerate SCF convergence. For ωB97X-3c calculations, a custom basis-set file was used which adds the missing basis functions for fluorine owing to the documented absence of fluorine in Psi4's internal implementation of vDZP.70

Molecule geometry optimizations were run using geomeTRIC 1.0.2,71 with the exception of protein optimizations, which were run using FIRE through the Atomic Simulation Environment (ASE).72 Periodic geometry optimizations were conducted using the ASE QuasiNewton optimizer and a Frechet cell filter, as applicable.

CPU timing studies were conducted on a 12-core Apple M3 Pro with 36 GB RAM, while GPU timing studies were conducted on a single NVIDIA A100 through the Modal cloud platform. Each calculation was run ten times in a row, and the average of the last five runs was taken as the reported time.

Results

Dataset Sensitivity

We began by testing the effect of different datasets on model performance. For initial model evaluation, we employed a set of benchmarks representative of our desired applications:

We compared the effect of adding different datasets to the core MACE-OFF23 dataset (Table 1). We observed the most significant improvement in GMTKN55 performance when we added the VectorQM24 dataset (V).48 VectorQM24 is a large set of ground-state main-group structures; adding VectorQM24 to MACE-OFF23 increased the total dataset size from 950K structures to 1.7M structures, and the number of unique structures from 19,228 to 98,896.

Extra DatasetExtra ElementsTotal StructuresUnique StructuresGMTKN55 ↓Baker Gradients ↑VIBFREQ1295 RMSE ↓
——9510011922827.170.996981.1
T C—10791722550727.120.9821105.9
VSi17358799889622.340.9731228.7
T C VSi186404610013923.560.9589238.0
V FSi17434309899627.670.9665266.1
D—12419003257863.840.98141467.2
SNa10434642446262.300.8373790.0

Table 1: Effect of adding auxiliary datasets (beyond the baseline M) on model performance. All datasets contain H, C, N, O, F, P, S, Cl, Br, and I. GMTKN55 scores are WTMAD-2, Baker gradient scores are mean cosine similarity, and VIBFREQ1295 scores are in cm-1.

Interestingly, this model performed substantially worse on gradients and frequencies than the MACE-OFF23-only model. We hypothesize that this occurs because all VectorQM24 structures are optimized structures with forces near zero. Since our loss function is a linear combination of force and energy error, we believe that this data may be biasing the model to make force predictions close to zero. This bias degrades gradient predictions, and by extension, frequency predictions. Similar effects have previously been reported by Bowen Deng and co-workers.76

We also experimented with adding a variety of transition-state datasets to our baseline dataset. Since the potential-energy surface near a transition state is quite different from other regions of the potential-energy surface, we hypothesized that including transition states in the dataset could dramatically improve model performance. We found that adding structures from Transition1x45 (T) and Coley3+246 (C) datasets led to improvements on the GMTKN55 transition-state subsets (like BHPERI and BHDIV)—the WTMAD-2 for the GMTKN55 barrier-height subsets decreased from 37.74 to 26.02. However, these improvements were offset by a slightly decreased gradient accuracy and a substantial decrease in the accuracy of frequency predictions. Previous work from Eric Yuan and co-workers has shown that adding transition-state structures to NNP datasets can degrade the quality of Hessian predictions, similar to the effect seen here.77

We hypothesized that adding non-equilibrium structures to the VectorQM24 dataset might attenuate the force-related errors observed, and that improved performance on barrier heights might complement the overall superior thermochemistry of the VectorQM24 model. This hypothesis proved to be false. Combining the transition-state datasets with the VectorQM24 dataset led to a model with worse predictions all around than either of the previous models; similarly, adding the highly non-equilibrium Finch dataset to VectorQM24 made the model worse. Efforts to add additional sources of dataset diversity (Denali and SPLINTER) also resulted in decreased model performance, even in domains where the data might presumably be added to help (e.g. non-covalent interactions for SPLINTER).44,47

Overall, the results of this dataset study seem to show that, at present margins, increasing dataset diversity leads to decreased overall performance. This conclusion is surprising, and we discuss it further below.

Model Size and Training Length

SizeCutoff Radius (Å)lmax\cal{l}_{\textbf{max}}*ChannelsParameters
Small4.5096748000
Medium5.011281400000
Large5.021923600000

Table 2: Hyperparameters for each model size in the training-length study. The final Egret-1 models were trained with the "Large" configuration, but the cutoff radius was increased to 6.0 Å.
*maximum spherical-harmonic degree used in the angular basis functions.

SizeEpochsGMTKN55 ↓Baker Gradients ↑VIBFREQ1295 MAE ↓VIBFREQ1295 RMSE ↓
Small2027.250.993036.178.7
Small4027.170.996935.281.6
Small19023.580.998832.983.5
Medium4024.360.999228.971.2
Medium12021.560.999428.375.0
Large4023.930.999727.367.7
Large8023.180.999927.369.9
Large12022.170.999927.469.0

Table 3: Performance comparison of Egret model sizes across training lengths. GMTKN55 results are reported as WTMAD-2, Baker gradient results are mean cosine similarity, and VIBFREQ1295 results (MAE and RMSE) are given in inverse centimeters.

We next studied the effect of model size and training length. Consistent with the results from MACE-OFF23,41 we observe that larger models perform better than smaller ones, and training longer improves performance on almost every benchmark. Curiously, we do not see this trend for the VIBFREQ1295 benchmark—in almost every case, the root-mean-squared error increased as training continued.

Based on these results, we selected three models for further study, all employing the "large" architecture: Egret-1, Egret-1e, and Egret-1t. Egret-1 is our recommended general-purpose model, trained on the MACE-OFF23 dataset. Egret-1e, trained on the MACE-OFF23 and VectorQM24 datasets, is best for thermochemistry and can also be used for molecules containing silicon. Finally, Egret-1t is best for transition-state calculations and was trained on the MACE-OFF23, Transition1x, and Coley3+2 datasets.

Thermochemistry and Barrier Heights

We assessed the performance of the Egret-1 models on subsets of the GMTKN55 set, which is commonly employed to benchmark new density functionals.73 After removing subsets outside of Egret-1's domain of applicability, 23 of the 55 subsets of GMTKN55 remained. We assessed the WTMAD-2 for various subsets of GMTKN55, as well as the overall WTMAD-2 (Table 4).

MethodTypeThermo Chem ↓Barrier Heights ↓NCI Intra- ↓NCI Inter- ↓Overall WTMAD-2 ↓
ωB97M-D3(BJ)aDFT5.602.493.634.314.01
r2SCAN-3cDFT5.568.647.115.676.67
B97-3cDFT11.058.6711.938.6910.39
GFN2-xTBSE21.1917.6511.4424.5819.44
AIMNet2NNP17.1411.8220.7512.2514.57
MACE-MP-0b2-LNNP20.1915.2020.7136.127.02
Orb-v3NNP13.5610.0517.6328.6721.42
OMat24 eqV2-LNNP88.2773.09659.5040.43221.17
SO3LRbNNP61.3623.49—21.66—
Egret-1NNP9.4535.6145.457.7220.91
Egret-1eNNP6.8928.1137.428.1617.40
Egret-1tNNP9.4513.9345.6210.1919.88

Table 4: GMTKN55 results (WTMAD-2) for the 23 in-distribution subsets.
aωB97M-D3(BJ)/def2-QZVP
bSO3LR model does not support Br, so the HAL59 subset cannot be run.

For tasks like reaction thermochemistry and intramolecular noncovalent interactions (NCIs), the Egret-1 models far outperform other NNPs and score similarly to quantum-chemical methods like B97-3c. Barrier heights—currently a challenge for NNPs76,77—are poorly described by Egret-1 and Egret-1e, which lack transition states in their training data, but adding transition-state data to Egret-1t dramatically improves the model's performance. While the breadth of systems included in GMTKN55 remains a challenge for today's NNPs, these results suggest that increasing the diversity of training data employed provides a path towards increasing NNP generality.

Much of the poor performance of the Egret-1 models on the intramolecular NCI dataset can be ascribed to three challenging datasets: CARBHB12, which examines hydrogen bonding between carbenes and small molecules; PNICO23, which looks at pnictogen bonding; and HAL59, which examines halogen bonding (Figure 2). These exotic interactions are poorly described in the training data, leading to poor model performance.

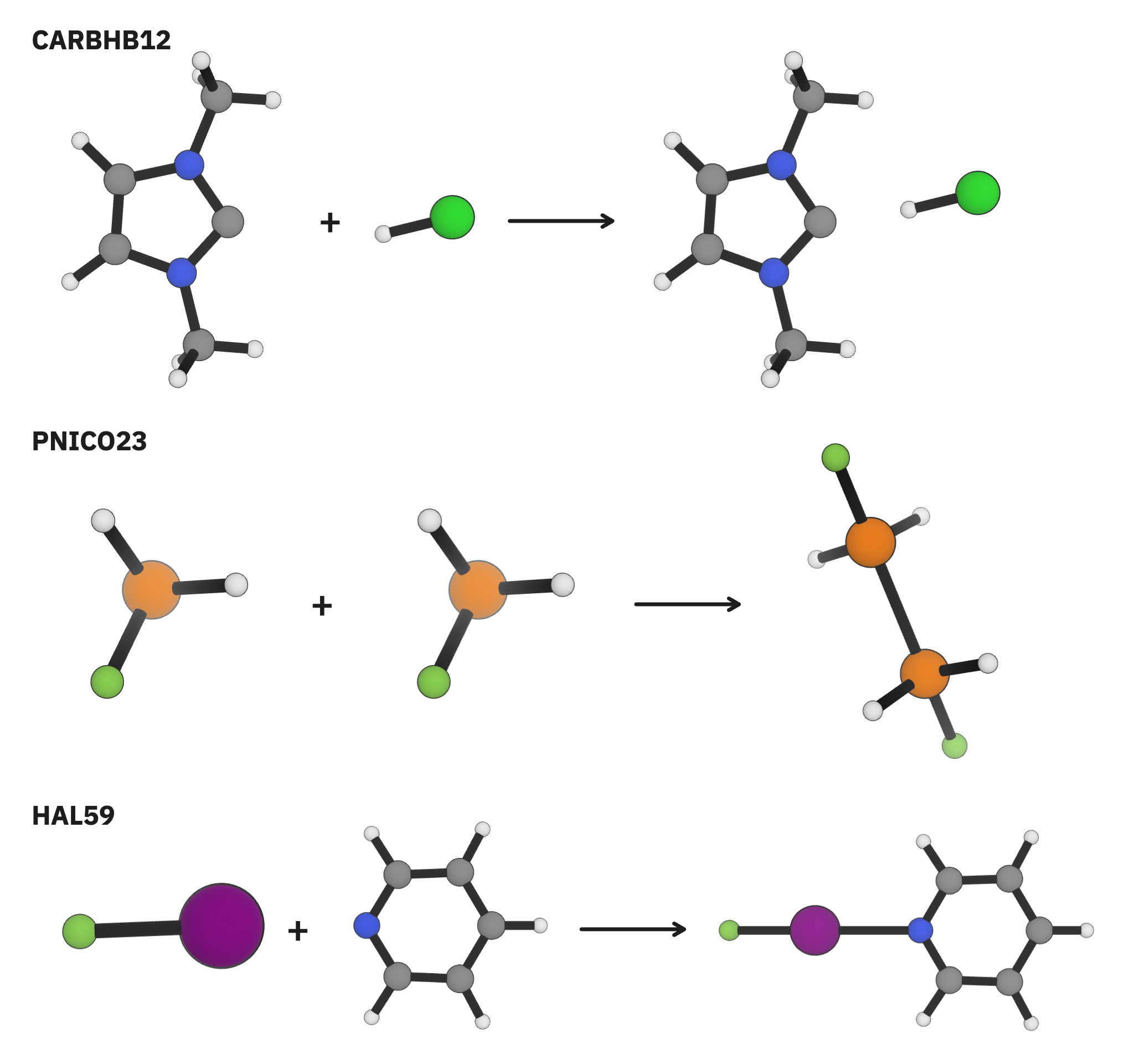
Several particularly challenging structures from the intermolecular non-covalent interaction subsets of GMTKN55.

Figure 2. Several particularly challenging structures from the intermolecular non-covalent interaction subsets of GMTKN55.

Molecular Geometries

To see if the Egret-1 models could be used to generate accurate molecular geometries, we benchmarked them against the ROT34 benchmark set.78 ROT34 tests the ability of computational methods to generate accurate gas-phase geometries through geometry optimization, as quantified by agreement with gas-phase rotational constants. Rotational constants are an exquisite probe of molecular geometry, as accurate prediction of rotational constants indicates that bond lengths, angles, and dihedral constants can all be reproduced correctly. The three Egret-1 models performed very well on ROT34, with mean absolute deviation and maximum deviation smaller than any other method surveyed, including composite density-functional-theory methods like r2SCAN-3c (Table 5).

MethodTheoryMD (%)MAD (%) ↓MAX (%) ↓SD (%) ↓
ωB97X-3cDFT−0.320.381.050.34
r2SCAN-3cDFT0.710.751.360.41
B97-3cDFT0.360.511.440.54
GFN2-xTBSE−1.542.8524.826.59
OpenFF SageFF3.003.139.322.07
AIMNet2NNP0.080.482.710.67
MACE-MP-0b2-LNNP2.012.115.671.19
Orb-v3NNP1.361.416.581.19
Egret-1NNP0.150.210.590.22
Egret-1eNNP0.160.240.520.22
Egret-1tNNP0.100.210.690.25

Table 5: ROT34 rotational constants benchmark results, reported as mean deviation (MD), mean absolute deviation (MAD), maximum deviation (MAX), and standard deviation (SD).

Vibrational Frequencies

We next sought to assess the accuracy of the Hessian matrices predicted by the Egret-1 models. Towards this end, we benchmarked the models against the VIBFREQ1295 dataset.75 After excluding molecules outside of Egret-1's domain of applicability, 115 molecules remained with reference vibrational frequencies computed at the CCSD(T)(F12*)/cc-pVDZ-F12 level of theory. We tested a variety of different levels of theory against this benchmark (Table 6).

MethodTheoryMAE ↓RMSE ↓
ωB97X-3cDFT41.053.5
r2SCAN-3cDFT22.331.1
B97-3cDFT32.644.5
GFN2-xTBSE66.486.7
AIMNet2NNP31.845.8
MACE-MP-0b2-LNNP94.2110.6
Orb-v3NNP64.476.7
Egret-1NNP24.449.2
Egret-1eNNP72.3161.9
Egret-1tNNP39.391.5

Table 6: VIBFREQ1295 vibrational frequency benchmark results (cm−1).

The three different Egret-1 models performed very differently on this benchmark: while Egret-1e performed poorly (similar to other low-cost methods), Egret-1t performed approximately as well as many commonly employed density functionals, and Egret-1 had one of the lowest mean errors of any method studied, exceeded only by the "Swiss-army-knife" composite DFT method r2SCAN-3c.

As discussed previously (vide supra), these results highlight the sensitivity of Hessian predictions to the precise dataset employed for training. Previous work from Eric Yuan and co-workers77 demonstrating that fine-tuning NNPs on transition-state geometries can result in a consistent underestimation of Hessian eigenvalues, which may explain the gap in performance between Egret-1 and Egret-1t. Similarly, Egret-1e adds a large number of equilibrium structures to the dataset, which may systematically bias the Hessian and gradient predictions. Alternative training strategies, like explicitly training to Hessian data,79 may ameliorate this sensitivity in the future.

Torsional Profiles

Accurate prediction of torsional profiles is an important and well-studied task in computer-assisted drug design. 80–82 We evaluated a variety of methods on the TorsionNet206 dataset, which comprises high-level CCSD(T)/def2-TZVP torsional scans for a library of drug-like fragments. We found that the Egret-1 models performed very well relative to other low-cost methods, and even exceeded the performance of common DFT methods like B3LYP-D3BJ/6-31G(d) and r2SCAN-3c. Given the clear effect of accurate torsional parameterization on the accuracy of free-energy-perturbation workflows80, we expect that Egret-1 can serve as a low-cost oracle method for torsional parameterization workflows like BespokeFit83 moving forward.

MethodTheoryMAE ↓RMSE ↓R2 ↑Spearman ↑
ωB97M-D3BJ/def2-TZVPPDDFT0.150.180.990.98
B97-3cDFT0.350.450.980.97
r2SCAN-3cDFT0.420.540.970.97
B3LYP-D3BJ/6-31G(d)DFT0.570.710.950.94
GFN2-xTBSE0.730.910.850.85
AIMNet2NNP0.390.480.950.94
MACE-MP-0b2-LNNP1.151.430.740.75
Orb-v3NNP0.971.200.830.83
OMat24 eqV2-LNNP1.481.840.770.81
Egret-1NNP0.200.240.990.98
Egret-1eNNP0.220.280.990.98
Egret-1tNNP0.230.290.990.98

Table 7: TorsionNet206 benchmark results; MAE and RMSE reported in kcal/mol, alongside R2 and Spearman correlation coefficients.

Conformers

Flexible molecules exist in a variety of different conformations. Predicting the energy differences between conformers is exceedingly difficult, as it is dominated by subtle changes in strain, solvation, and van der Waals forces. Accurately determining the ground-state conformer and the Boltzmann distribution of conformers is vital for predicting strain energy in docked poses, conformationally averaged properties, and downstream reaction modeling.84–87

Representative conformer ensembles from the Folmsbee benchmark set.

Figure 3. Representative conformer ensembles from the Folmsbee benchmark set.

We employed three different conformer-based benchmarks to assay the performance of the Egret-1 models at this important task. We first benchmarked Egret-1 on the large Folmsbee conformer set,12 which comprises 708 distinct conformer ensembles computed at the DLPNO-CCSD(T) level of theory (Figure 3). After removing charged species and ensembles for which the DLPNO calculations were not completed, 593 of the 708 ensembles remained. We found that the Egret-1 models had similar performance to DFT methods like B97-3c and far outperformed existing NNPs like AIMNet2, Orb-v3, and MACE-MP-0b2-L (Table 8).

MethodTheoryOverall MAE ↓Overall RMSE ↓Mean R2 ↑Mean Spearman ↑Incomplete Subsets
ωB97X-D/def2-TZVPDFT0.240.370.840.854
B3LYP/def2-TZVPDFT0.250.390.840.85—
B97-3cDFT0.300.490.810.821
GFN2-xTBSE0.711.290.570.60—
AIMNet2NNP0.540.930.640.65—
MACE-MP-0b2-LNNP1.082.060.460.37—
Orb-v3NNP0.881.710.510.50—
OMat24 eqV2-LNNP0.871.440.470.50—
Egret-1NNP0.310.510.780.81—
Egret-1eNNP0.300.500.790.81—
Egret-1tNNP0.340.590.760.79—

Table 8: Folmsbee conformer-energy benchmark; MAE and RMSE reported in kcal/mol.

The Folmsbee conformer set focuses on low-energy conformers: the vast majority of Folmsbee conformers are within 5 kcal/mol of the ground state. A contrasting conformer benchmark is Wiggle150,23 which comprises 150 highly strained conformers of three organic molecules (average relative energy of 103 kcal/mol) and tests the ability of NNPs to handle unusual bond distances and angles (Figure 4).

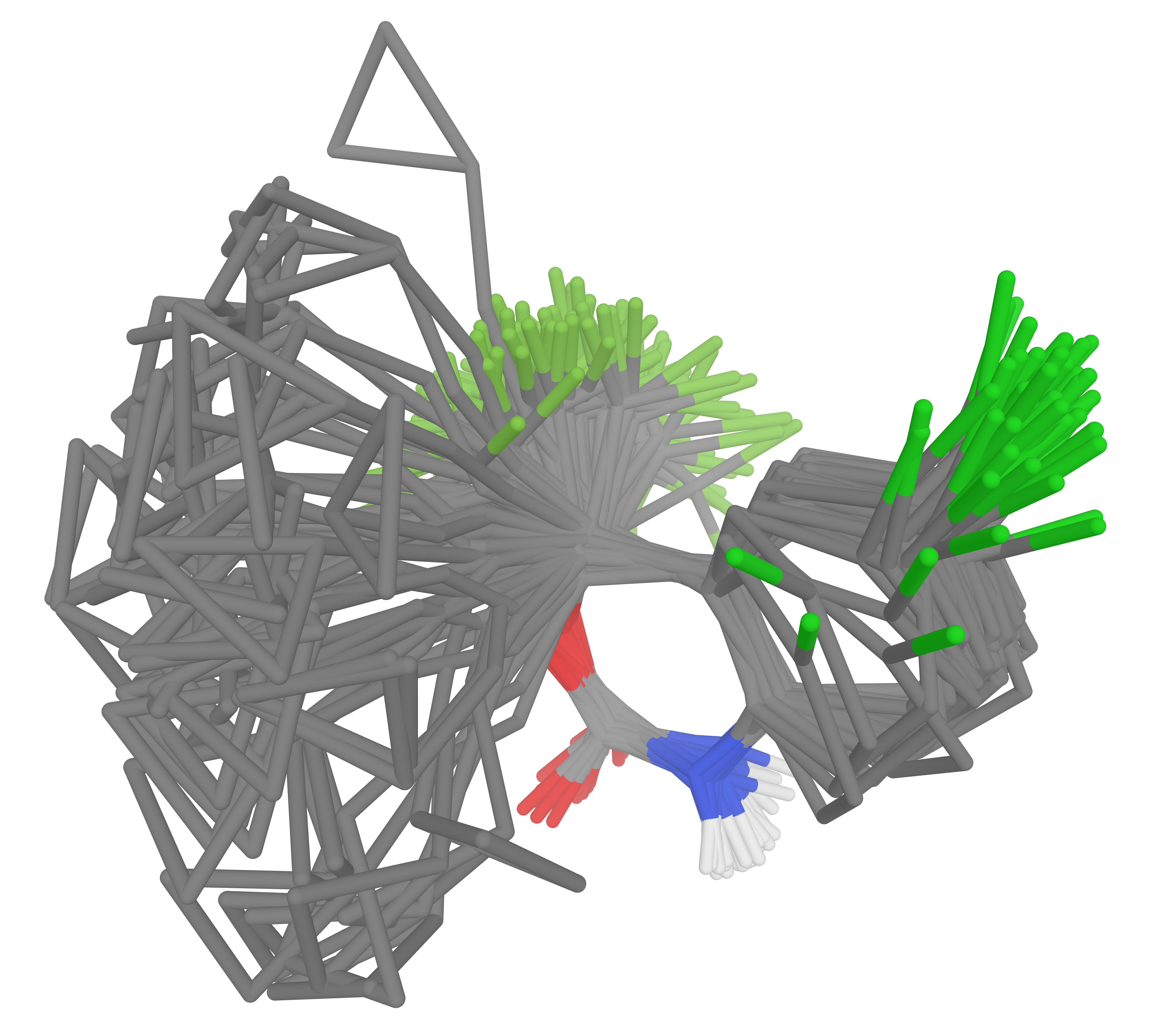
Efavirenz conformers from the Wiggle150 benchmark set.

Figure 4. Efavirenz conformers from the Wiggle150 benchmark set.

We evaluated the performance of Egret-1 and other NNPs against Wiggle150 (Table 9). All Egret-1 models performed better than any other NNP surveyed on Wiggle150, and even outperformed most DFT methods: only double hybrids or range-separated hybrids with quadruple-ζ\zeta basis sets scored better than the best Egret-1 models.

MethodTheoryMAE ↓RMSE ↓
ωB97M-D3BJ/def2-QZVPDFT1.181.59
ωB97X-3cDFT4.124.63
r2SCAN-3cDFT1.722.19
B97-3cDFT2.322.96
B3LYP-D3BJ/6-31G(d)DFT3.464.01
GFN2-xTBSE14.6015.20
Sage 2.2.1FF27.2034.60
AIMNet2NNP2.353.11
MACE-MP-0b2-LNNP14.5916.37
Orb-v3NNP7.728.82
OMat24 eqV2-LNNP6.367.73
SO3LRNNP10.3612.36
Egret-1NNP1.582.15
Egret-1eNNP1.562.07
Egret-1tNNP1.712.25

Table 9: Wiggle150 strained-conformer benchmark; MAE and RMSE reported in kcal/mol.

Finally, we tested Egret-1's ability to handle complex bioorganic structures through Řezáč's MPCONF196 benchmark, which comprises 196 conformers of 13 complex macrocyclic therapeutics (Figure 5).88 Organic macrocycles can exhibit exceedingly complex conformational behavior89–92 and present a particularly challenging test for computational methods—but accurate description of conformational behavior is critical to rational design of macrocyclic therapeutics.93,94 Egret-1 far outperformed all other NNPs on this benchmark, with an MAE and RMSE comparable to density-functional-theory methods with quadruple-ζ\zeta basis sets (Table 10).

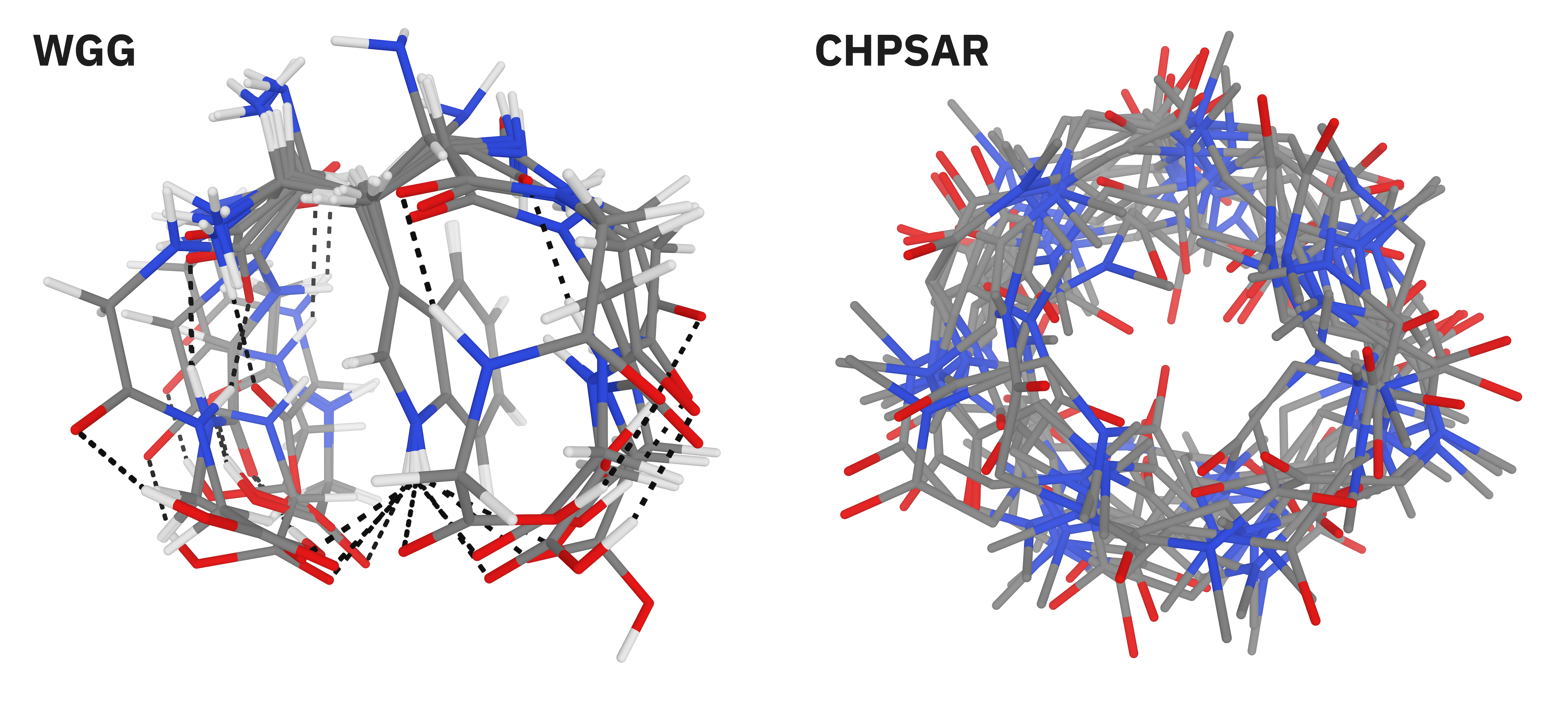
Representative macrocyclic conformer ensembles from the MPCONF196 benchmark set.

Figure 5. Representative macrocyclic conformer ensembles from the MPCONF196 benchmark set.

MethodTheoryMAE ↓RMSE ↓
ωB97X-D3/def2-QZVPDFT0.641.06
B3LYP-D3BJ/def2-QZVPDFT0.620.92
M06-2X/def2-QZVPDFT1.562.23
GFN2-xTBSE2.213.14
AIMNet2NNP2.062.71
MACE-MP-0b2-LNNP4.916.42
Orb-v3NNP3.945.32
Egret-1NNP0.701.12
Egret-1eNNP1.031.50
Egret-1tNNP0.931.45

Table 10: MPCONF196 macrocycle conformer-energy benchmark; MAE and RMSE reported in kcal/mol.

Molecular Dynamics

Accurate prediction of many chemical phenomena requires molecular dynamics (MD). Unfortunately, good performance on energy- and force-based benchmarks is not enough to guarantee that an NNP will be able to produce stable, well-defined MD trajectories; in 2022, Xiang Fu and co-workers showed that "many existing models are inadequate when evaluated on simulation-based benchmarks, even when they show accurate force prediction" and argued that direct MD-based testing should be employed in the future.95 In the subsequent years, short MD simulations have become a quick and practical way to assay if a given NNP leads to stable simulations or causes energy leaks and runaway heating.96–98

We evaluated the stability of the Egret-1 models on MD simulations of maraviroc, an anti-retroviral therapeutic emblematic of the complex drug-like molecules Egret-1 is intended to study. Simulations were run in the NVT ensemble for 1 ps using a second-order Langevin thermostat,99 and then propagated for 100 ps in the NVE ensemble using velocity Verlet integration with a 1 fs timestep. We found that all Egret-1 models were stable for the entire 100 ps studied. While further work is needed to assess MD stability on a more varied set of tasks, this experiment rules out the catastrophic energy-leakage scenarios characteristic of previous generations of NNPs.

Periodic Systems

We next investigated if the Egret-1 models were capable of extrapolation to periodic systems. Today, the divide between molecular and periodic quantum chemistry has given rise to two largely separate ecosystems of researchers, software, and publications.100 Hybrid density functionals, although typically more accurate101,102 than non-hybrid density functionals for molecular systems, are impractical to employ for all but the smallest periodic systems;103 most periodic calculations are instead run with non-hybrid density functionals, which is known to create substantial errors in inter alia small-molecule conformations.104

Graph-based NNPs provide a potential way to connect these two paradigms. Previous work from Kästner105 and Daru106 suggests that NNPs trained on high-accuracy molecular DFT calculations might be able to extrapolate to periodic systems, thus providing scientists with a way to extend the accuracy of hybrid molecular DFT to periodic systems. To assess the accuracy of the Egret-1 models at simulating periodic systems, we employed the X23b benchmark set,107,108 which tests the ability of computational methods to reproduce experimental lattice energies and unit-cell volumes for 23 organic molecular crystals (Table 11).

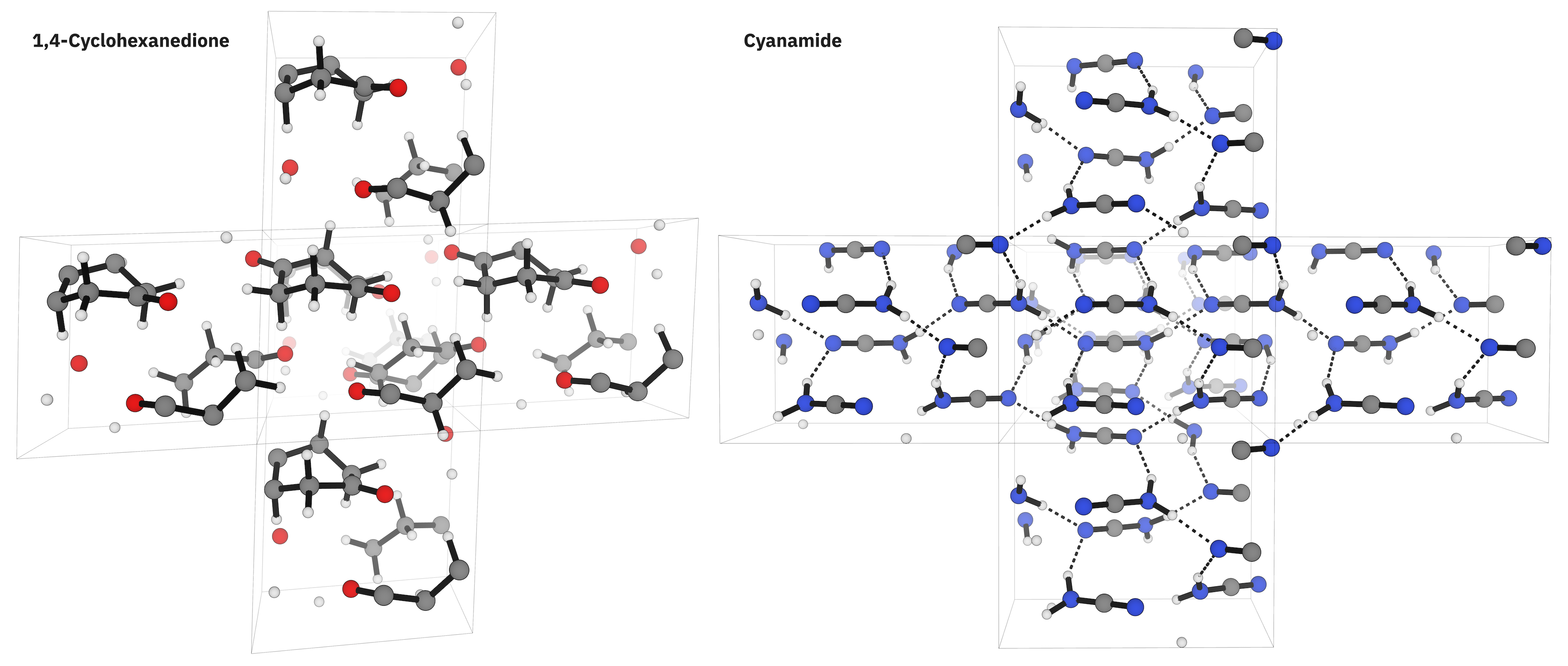
1,4-cyclohexanedione and cyanamide structures from the X23b benchmark set.

Figure 6. 1,4-cyclohexanedione and cyanamide structures from the X23b benchmark set.

While Egret-1e and Egret-1t performed very poorly on this benchmark set, we found that Egret-1 was the best-performing NNP studied, with a mean-absolute-error for lattice energy of 2.61 kcal/mol. Nevertheless, a considerable gap between low-cost methods and density-functional theory still exists for this task, indicating that achieving chemical accuracy for periodic calculations remain an unsolved challenge for these NNPs.

MethodTheoryLattice Energy MAE ↓Cell Volume MAPE (%) ↓
r2SCAN-3cDFT0.973.68
PBE-D4/QZ // PBE-D4/mTZDFT0.874.44
GFN2-xTBSE5.387.76
AIMNet2NNP9.4418.52
MACE-MP-0b2-L (with D3BJ)NNP3.473.03
MACE-MP-0b2-L (no D3BJ)NNP9.2822.39
Orb-v3NNP26.7912.30
Egret-1NNP2.614.38
Egret-1eNNP18.6614.73
Egret-1tNNP30.1912.11

Table 11: X23b molecular-crystal benchmark. Lattice energy is reported as mean absolute error (MAE) in kcal/mol; cell volume is reported as mean absolute percent error (MAPE).

Prediction of relative crystal-polymorph stability is crucial in drug formulation; in pathological cases like Abbott's anti-HIV drug ritonavir, the presence of unexpected low-energy polymorphs can lead to catastrophic manufacturing failure and hundreds of millions of dollars in estimated losses.1,109 An Abbott postmortem concluded that it was "highly advisable… to carry on exhaustive research to identify the most stable and all possible polymorphs" to prevent future ritonavir-level crises,1 and consequently experimental and computational methods for crystal-polymorph exploration have become key technologies in small-molecule process research and development, even though the requisite periodic DFT calculations typically require millions of CPU-hours on high-performance computing clusters.110

To assess Egret-1's ability to accurately identify low-energy crystal polymorphs, we evaluated it on a recent set of organic crystal polymorphs collected by Schrödinger and ranked with the r2SCAN functional.111 After excluding the pathological PULWIF structure, which led to erratic results with all methods surveyed, 63 sets of crystal polymorphs remained in our benchmark set (Table 12). Energy- and ranking-based benchmarks were computed separately for all 63 sets and then averaged to give the final values shown below.

MethodMAE ↓RMSE ↓R2 ↑Spearman ↑
AIMNet22.072.430.270.30
MACE-MP-0b2-L0.740.910.270.28
Orb-v30.760.940.250.26
Egret-10.760.970.340.33

Table 12: Schrödinger crystal-polymorph-ranking benchmark; MAE and RMSE reported in kcal/mol, alongside R2 and Spearman correlation coefficients.

While AIMNet2 performs poorly on this benchmark, the other three NNPs all achieve good relative accuracy here (as assessed by MAE and RMSE), but the large number of accessible low-lying polymorphs leads to poor Pearson and Spearman correlation values. We note that as described above,104,112 non-hybrid functionals often struggle with relative conformer energies, so the reference r2SCAN data may be somewhat inaccurate—the uniform c. 0.7 kcal/mol MAE may reflect a limitation of this benchmark set. Future work can study if methods like Egret-1 can be integrated into end-to-end crystal-structure-prediction workflows to increase efficiency and accuracy; recent results from Schrödinger indicate that NNPs can be gainfully employed as an intermediate filtering step before running full DFT calculations.111

Timing

A key advantage of NNPs relative to conventional quantum-chemical methods like DFT is the potential for dramatic speed increases. To assess the magnitude of the speedups possible with the Egret-1 models, we measured the speed of Egret-1 as compared to other levels of theory (Table 13). While Egret-1 is relatively slow compared to NNPs without equivariance or with fewer parameters, it remains significantly faster than even low-accuracy DFT methods with double-ζ\zeta basis sets like B3LYP/6-31G(d).

MethodTheoryComputeIbuprofen (s)Citalopram (s)Rapamycin (s)Insulin (s)
B3LYP/6-31(G)DFTCPU17.34176.88867.14Failed
GFN2-xTBSECPU0.050.080.42Failed
AIMNet2NNPCPU0.050.140.070.22
AIMNet2NNPGPU0.080.080.080.08
MACE-MP-0b2-LNNPCPU0.300.670.965.62
MACE-MP-0b2-LNNPGPU0.280.290.280.43
Orb-v3NNPCPU0.510.540.675.42
Orb-v3NNPGPU0.270.280.310.28
Egret-1tNNPCPU0.811.311.8012.50
Egret-1tNNPGPU0.850.861.011.09

Table 13: Time to compute a single-point energy by level of theory, in seconds.

Egret-1 also does not suffer from the SCF- and band-gap-related pathologies of DFT for large biomolecular systems,113 allowing for smooth and well-behaved optimizations to be easily conducted even on small proteins. Following sanitization and removal of water molecules, we were able to optimize an all-atom structure of human insulin (PDB: 3I40)114 using the FIRE optimizer in 140 seconds and 716 optimization steps on a single NVIDIA H100 (Figure 7).115

Comparison of initial (red) and optimized (blue) all-atom human insulin structures.

Figure 7. Comparison of initial (red) and optimized (blue) all-atom human insulin structures.

Catalysis

NNPs offer the promise of modeling larger systems than can currently be accessed with DFT with significantly fewer computational resources. In 2017, Daniel DiRocco and co-workers at Merck reported the development of a multifunctional organocatalyst for stereoselective prodrug assembly.116 Kinetic studies demonstrated catalyst cooperativity, leading DiRocco and co-workers to develop a preorganized dimeric catalyst that displayed significantly increased activity. As a part of this study, the authors found transition states with DFT for these large supramolecular assemblies, reporting a ΔΔG‡ for the two isomers of 2.3 kcal/mol for their initial catalyst and 2.6 kcal/mol for the linked dimeric catalyst. While the size of this system meant that even a single-point calculation with the ωB97X-3c DFT functional took over two hours, reoptimization of the transition state with Egret-1 could be run in under a minute on a consumer-grade NVIDIA RTX 4090 GPU. Egret-1 showed a highly conserved structure during re-optimization, but like all of the tested low-cost methods, overstabilized the lower-energy TS (Table 14).

MethodTheoryΔΔG‡ (Separate)ΔΔG‡ (Linked)
ReferenceaDFT2.292.60
GFN2-xTBSE3.094.72
AIMNet2NNP3.9210.17
Egret-1NNP5.726.37
Egret-1eNNP8.8710.33
Egret-1tNNP7.9611.25

Table 14: Gibbs free-energy difference between diastereomers of the transition state.
aM06L/6-31+G(d,p)//B3LYP-D3/6-31G(d,p)

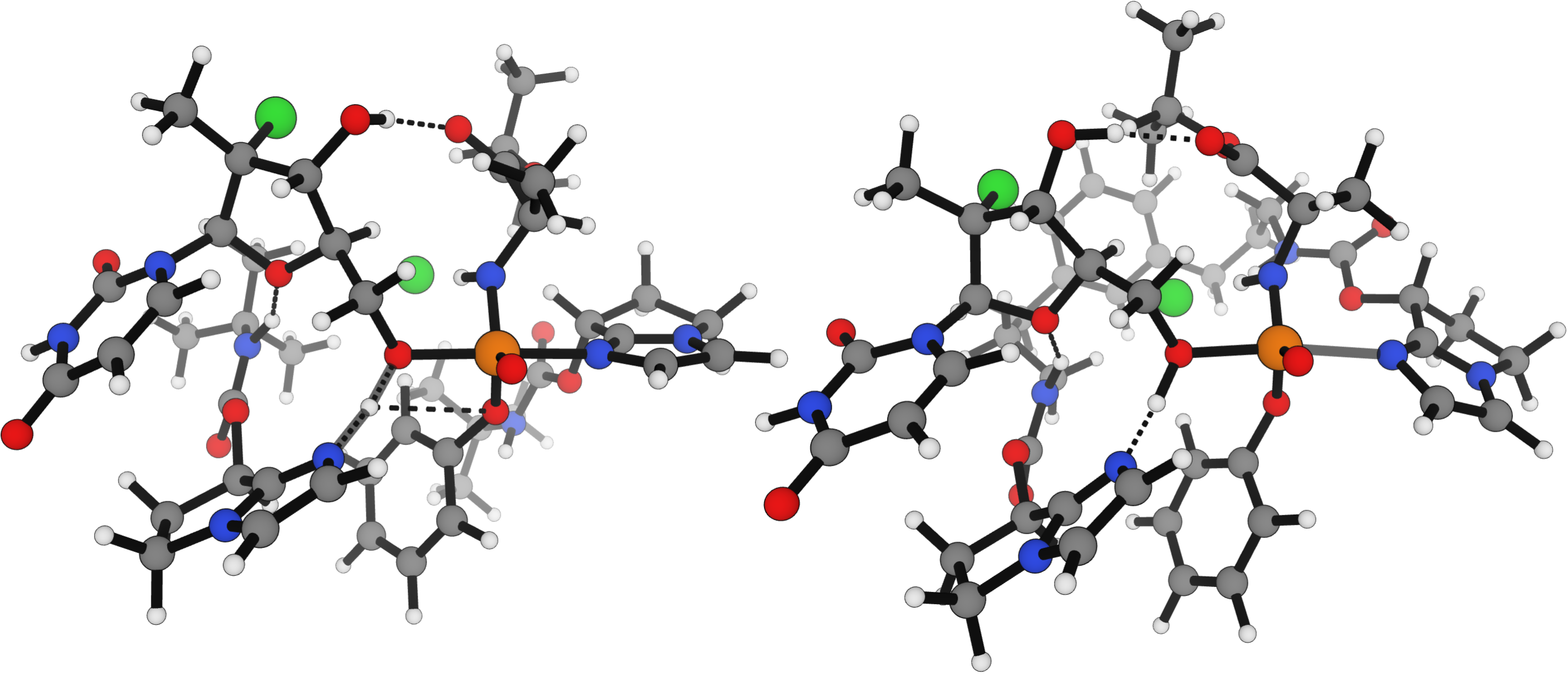
Egret-1 computed structures of the DiRocco transition states for the separate catalysts (left) and linked dimeric catalyst (right).

Figure 8. Egret-1 computed structures of the DiRocco transition states for the separate catalysts (left) and linked dimeric catalyst (right).

Discussion

In this work, we have shown that the Egret-1 models are capable of serving as drop-in replacements for DFT in a variety of applications important to drug discovery and materials science. Surprisingly, no massive fundamental advance in dataset scale or model architecture was necessary to achieve this result—we simply combine previously reported datasets with a well-studied model architecture, with a focus on maximizing accuracy.

Our models occupy a distinct niche in the emerging landscape of ML-based atomistic simulation methods. We focus on maximizing zero-shot accuracy versus experimental or high-level quantum-chemical benchmarks, not on inference speed or data efficiency; accordingly, we anticipate that the near-term use of the Egret-1 models will center around using them as fast surrogates for DFT, not as replacements for forcefields. This focus differs from other recent work in the field, like the optimized Orb models from Mark Neumann and coworkers at Orbital Materials64,65 or Ishan Amin and co-workers' development of student–teacher model-distillation strategies.97 In the future, cross-pollination between these different efforts will hopefully lead to the development of models which inherit the best characteristics of both.

Egret-1 is limited to predictions of energies, forces, and derivatives thereof (like frequencies). While these are by far the most commonly simulated properties, the lack of dipole moments, atom-centered charges, and other electronic properties limits the applicability of these models to certain tasks. Egret-1 also is only trained on gas-phase calculations and thus predicts properties only in the gas phase; we plan to address this limitation in the future, either through fine-tuning or by using an auxiliary solvent-correction model like GNNIS.117,118

Our work also illustrates important outstanding challenges in the NNP field. Unlike many domains of machine learning, atomistic simulation appears to not yet have reached a scale in which increasing dataset size has a uniformly positive effect. In many cases, adding data could be shown to reduce the performance of the model on virtually every test set, including benchmarks which appear similar to the new data. Even in cases when adding more data improved relevant benchmark scores, these improvements were often offset by losses in some other area—for instance, Egret-1e is best at thermochemistry, but produces significantly inferior frequencies. This "zero-sum" model behavior may suggest that more expressive architectures are needed for further systematic improvements—or simply that the scale of the Egret-1 models is insufficient.

We hypothesize that better training strategies and dataset-aggregation strategies will be key to continued improvement with today's datasets. While all of the models described in this work use a single-phase training procedure, more complex pretraining and fine-tuning protocols may make it possible to increase diversity by introducing new data distributions without causing catastrophic losses in general performance. We note that our observations are limited to a single architecture, and that dataset sensitivity may differ across architectures.

This study highlights the need for better ways to quantify diversity and similarity in training datasets. Here, we were able to identify productive combinations of existing datasets through essentially a trial-and-error approach, which quickly becomes expensive, time-consuming, and impractical. Data-driven methods to guide the construction of new, well-behaved datasets would be immensely valuable for future efforts, particularly because adding even small amounts of new data to a well-behaved dataset can result in substantial performance degradation. For example, simple heuristics about the optimal ratio of near-equilibrium to far-from-equilibrium structures to include, the optimal number of conformers per molecule, the best way to include transition states and other reaction-path structures, and so on would vastly simplify the process of creating new datasets and training more general NNPs moving forward.119

Our experience training the Egret-1 models also reinforces the importance of evaluating non-energy-based benchmarks throughout the training process. Based solely on energy benchmarks, we might easily have concluded that Egret-1e or a similar model was best, and discovered only later on that the gradients and frequencies were inaccurate—the sensitivity of these higher-order properties of the potential-energy surface to dataset construction makes it imperative to continuously monitor them. We observed a similar phenomenon when training EquiformerV2 models on this dataset.120

Conclusion

In this work, we report the Egret-1 family of neural network potentials, which aim to achieve zero-shot chemical accuracy for closed-shell bioorganic simulation tasks. Our benchmarks show that Egret-1 achieves this goal for many important simulation tasks—and, in many circumstances, Egret-1 is more accurate than the small-basis-set quantum-chemical methods routinely employed in academic research, drug discovery, and materials science. The models presented here can thus serve as replacements for quantum chemistry in many contexts, even without system-specific fine-tuning.

The Egret-1 models are available at github.com/rowansci/egret-public under an MIT license and can also be run through the Rowan computational-chemistry platform. While we have spent considerable time benchmarking these models on a wide variety of challenging tasks, we expect that broader scientific usage will be indispensable in driving further improvements, and look forward to learning more about these models' strengths and weaknesses.

The Egret-1 models have several obvious lacunae—such as being limited to relatively few elements and neutral closed-shell molecules in the gas phase—which we plan to address in the future. These models are also too slow for many important workflows, like molecular dynamics studies of large biomolecules or polymers, which limits their applicability and utility. Thus, while we feel this work represents an important step towards the "holy grail" of fast, accurate, and reliable molecular simulation,2 many more steps will be needed to fully achieve the goals outlined in the introduction. In particular, we anticipate that a combination of improved dataset scale and quality, more expressive architectures, and performance optimization will make it possible to achieve significantly improved accuracy, speed, and generality, which we expect to have a substantial impact on discovery across the chemical sciences.

Acknowledgments

The authors thank Keir Adams, Justin Airas, Ilyes Batatia, Simon Batzner, Cristian Bodnar, Jackson Burns, Tim Duignan, Zach Fried, Joe Gair, Ishaan Ganti, Kevin Greenman, Chandler Greenwell, Michael Hla, Patrick Hsu, Bowen Jing, David Klee, Veljko Kovac, Tony Kulesa, Eugene Kwan, Eli Laird, Yi-Lun Liao, Abhishaike Mahajan, Narbe Mardirossian, Alex Mathiasen, Tom McGrath, Gabriel Mongaras, Albert Musaelian, Mark Neumann, Vedant Nilabh, Sam Norwood, John Parkhill, Andrew Rosen, Marcus Sak, Justin Smith, Guillem Simeon, Hannes Stärk, Kayvon Tabrizi, Zach Ulissi, Nick Wall & Larry Zitnik for helpful discussions, and Tim Duignan, Joe Gair, Michael Hla, Alex Mathiasen, Mark Neumann, & Marcus Sak for editing early drafts of this manuscript.

Bibliography

  1. Chemburkar, S. R. et al. Dealing with the impact of ritonavir polymorphs on the late stages of bulk drug process development. Organic Process Research & Development 2000, 4, 5, 413–417.
  2. Houk, K.; Liu, F. Holy grails for computational organic chemistry and biochemistry. Accounts of Chemical Research 2017, 50, 3, 539–543.
  3. Van Drie, J. H. Computer-aided drug design: the next 20 years. Journal of Computer-Aided Molecular Design 2007, 21, 10, 591–601.
  4. Stephenson, N. The Diamond Age; Bantam Books:, 1995.
  5. Gao, H.; Imamura, S.; Kasagi, A.; Yoshida, E. Distributed implementation of full configuration interaction for one trillion determinants. Journal of Chemical Theory and Computation 2024, 20, 3, 1185–1192.
  6. Pederson, R. et al. Large Scale Quantum Chemistry with Tensor Processing Units. Journal of Chemical Theory and Computation 2022, 19, 1, 25–32. DOI: 10.1021/acs.jctc.2c00876
  7. Stocks, R.; Vallejo, J. L. G.; Fiona, C.; Snowdon, C.; Palethorpe, E.; Kurzak, J.; Bykov, D.; Barca, G. M. Breaking the Million-Electron and 1 EFLOP/s Barriers: Biomolecular-Scale Ab Initio Molecular Dynamics Using MP2 Potentials. SC24: International Conference for High Performance Computing, Networking, Storage and Analysis 2024, 1–12. DOI: 10.1109/SC41406.2024.00015
  8. Galvez Vallejo, J. L. et al. Toward an extreme-scale electronic structure system. The Journal of Chemical Physics 2023, 159, 4, 044112. DOI: 10.1063/5.0156399
  9. Wagen, C. Conventional Chemical Simulation Is Too Slow, and ML Can Help. https://rowansci.com/blog/conventional-chemical-simulation-too-slow (accessed 2025-05-01).
  10. Mahajan, A. A primer on molecular dynamics. https://www.owlposting.com/p/a-primer-on-molecular-dynamics (accessed 2025-05-01).
  11. Kanal, I. Y.; Keith, J. A.; Hutchison, G. R. A sobering assessment of small-molecule force field methods for low energy conformer predictions. International Journal of Quantum Chemistry 2018, 118, 5, e25512. DOI: 10.1002/qua.25512
  12. Folmsbee, D.; Hutchison, G. Assessing conformer energies using electronic structure and machine learning methods. International Journal of Quantum Chemistry 2021, 121, 1, e26381. DOI: 10.1002/qua.26381
  13. Winkler, L.; Galindo-Murillo, R.; Cheatham, T. E. I. Structures and Dynamics of DNA Mini-Dumbbells Are Force Field Dependent. Journal of Chemical Theory and Computation 2023, 19, 8, 2198-2212. DOI: 10.1021/acs.jctc.3c00130
  14. Nadeem, H.; Shukla, D. Ensemble Adaptive Sampling Scheme: Identifying an Optimal Sampling Strategy via Policy Ranking. Journal of Chemical Theory and Computation. DOI: 10.1021/acs.jctc.4c01488
  15. Piana, S.; Lindorff-Larsen, K.; Shaw, D. E. How Robust Are Protein Folding Simulations with Respect to Force Field Parameterization?. Biophysical Journal 2011, 100, 9, L47-L49. DOI: 10.1016/j.bpj.2011.03.051
  16. Moore, J. H.; Cole, D. J.; Csanyi, G. Computing hydration free energies of small molecules with first principles accuracy. arXiv preprint arXiv:2405.18171 2024. DOI: 10.48550/arXiv.2405.18171
  17. Rufa, D. A.; Bruce Macdonald, H. E.; Fass, J.; Wieder, M.; Grinaway, P. B.; Roitberg, A. E.; Isayev, O.; Chodera, J. D. Towards chemical accuracy for alchemical free energy calculations with hybrid physics-based machine learning molecular mechanics potentials. bioRxiv 2020. DOI: 10.1101/2020.07.29.227959
  18. Behler, J.; Parrinello, M. Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Physical Review Letters 2007, 98, 146401. DOI: 10.1103/PhysRevLett.98.146401
  19. Morawietz, T.; Sharma, V.; Behler, J. A neural network potential-energy surface for the water dimer based on environment-dependent atomic energies and charges. The Journal of Chemical Physics 2012, 136, 6.
  20. Smith, J. S.; Isayev, O.; Roitberg, A. E. ANI-1: an extensible neural network potential with DFT accuracy at force field computational cost. Chemical Science 2017, 8, 4, 3192–3203.
  21. Behler, J. Four Generations of High-Dimensional Neural Network Potentials. Chemical Reviews 2021, 121, 16, 10037-10072. DOI: 10.1021/acs.chemrev.0c00868
  22. Duval, A. et al. A hitchhiker's guide to geometric gnns for 3d atomic systems. arXiv preprint arXiv:2312.07511 2023. DOI: 10.48550/arXiv.2312.07511
  23. Brew, R. R.; Nelson, I. A.; Binayeva, M.; Nayak, A. S.; Simmons, W. J.; Gair, J. J.; Wagen, C. C. Wiggle150: Benchmarking Density Functionals and Neural Network Potentials on Highly Strained Conformers. Journal of Chemical Theory and Computation 2025, 21, 8, 3922-3929. DOI: 10.1021/acs.jctc.5c00015
  24. Wagen, A. NNP Arena. https://benchmarks.rowansci.com/ (accessed 2025-05-01).
  25. Pople, J. A. Nobel lecture: Quantum chemical models. Reviews of Modern Physics 1999, 71, 5, 1267.
  26. Wang, Y. et al. On the design space between molecular mechanics and machine learning force fields. Applied Physics Reviews 2025, 12, 2. DOI: 10.1063/5.0237876
  27. Musaelian, A.; Batzner, S.; Johansson, A.; Sun, L.; Owen, C. J.; Kornbluth, M.; Kozinsky, B. Learning local equivariant representations for large-scale atomistic dynamics. Nature Communications 2023, 14, 1, 579.
  28. Simeon, G.; Mirarchi, A.; Pelaez, R. P.; Galvelis, R.; De Fabritiis, G. Broadening the Scope of Neural Network Potentials through Direct Inclusion of Additional Molecular Attributes. Journal of Chemical Theory and Computation 2025. DOI: 10.1021/acs.jctc.4c01625
  29. Unke, O. T.; Chmiela, S.; Sauceda, H. E.; Gastegger, M.; Poltavsky, I.; Schütt, K. T.; Tkatchenko, A.; Müller, K. Machine Learning Force Fields. Chemical Reviews 2021, 121, 16, 10142-10186. DOI: 10.1021/acs.chemrev.0c01111
  30. Eastman, P.; Pritchard, B. P.; Chodera, J. D.; Markland, T. E. Nutmeg and SPICE: Models and Data for Biomolecular Machine Learning. Journal of Chemical Theory and Computation 2024, 20, 19, 8583-8593. DOI: 10.1021/acs.jctc.4c00794
  31. Lee Warren, G.; Davis, J. E.; Patel, S. Origin and control of superlinear polarizability scaling in chemical potential equalization methods. The Journal of Chemical Physics 2008, 128, 14, 144110. DOI: 10.1063/1.2872603
  32. Cheng, B. Latent Ewald summation for machine learning of long-range interactions. npj Computational Materials 2025, 11, 1, 80. DOI: 10.1038/s41524-025-01577-7
  33. Yu, H.; Hong, L.; Chen, S.; Gong, X.; Xiang, H. Capturing long-range interaction with reciprocal space neural network. arXiv preprint arXiv:2211.16684 2022. DOI: 10.48550/arXiv.2211.16684
  34. Frank, J. T.; Unke, O. T.; Müller, K. So3krates: Equivariant attention for interactions on arbitrary length-scales in molecular systems. arXiv preprint arXiv:2205.14276 2022. DOI: 10.48550/arXiv.2205.14276
  35. Nakago, K. Neural network potential with charge transfer. https://tech.preferred.jp/en/blog/neural-network-potential-with-charge-transfer (accessed 2025-05-01).
  36. Zhong, P.; Kim, D.; King, D. S.; Cheng, B. Machine learning interatomic potential can infer electrical response. arXiv preprint arXiv:2504.05169 2025.
  37. Kim, D.; King, D. S.; Zhong, P.; Cheng, B. Learning charges and long-range interactions from energies and forces. arXiv preprint arXiv:2412.15455 2024.
  38. Yao, K.; Herr, J. E.; Toth, D. W.; Mckintyre, R.; Parkhill, J. The TensorMol-0.1 model chemistry: a neural network augmented with long-range physics. Chemical Science 2018, 9, 8, 2261–2269.
  39. Najibi, A.; Goerigk, L. The nonlocal kernel in van der Waals density functionals as an additive correction: An extensive analysis with special emphasis on the B97M-V and ωB97M-V approaches. Journal of Chemical Theory and Computation 2018, 14, 11, 5725–5738. DOI: 10.1021/acs.jctc.8b00842
  40. Hellweg, A.; Rappoport, D. Development of new auxiliary basis functions of the Karlsruhe segmented contracted basis sets including diffuse basis functions (def2-SVPD, def2-TZVPPD, and def2-QVPPD) for RI-MP2 and RI-CC calculations. Physical Chemistry Chemical Physics 2015, 17, 2, 1010–1017. DOI: 10.1039/C4CP04286G
  41. Kovács, D. P. et al. MACE-OFF23: Transferable machine learning force fields for organic molecules. arXiv preprint arXiv:2312.15211 2023.
  42. Eastman, P. et al. Spice, a dataset of drug-like molecules and peptides for training machine learning potentials. Scientific Data 2023, 10, 1, 11.
  43. Isert, C.; Atz, K.; Jiménez-Luna, J.; Schneider, G. QMugs, quantum mechanical properties of drug-like molecules. Scientific Data 2022, 9, 1, 273. DOI: 10.1038/s41597-022-01390-7
  44. Christensen, A. S. et al. OrbNet Denali: A machine learning potential for biological and organic chemistry with semi-empirical cost and DFT accuracy. The Journal of Chemical Physics 2021, 155, 20. DOI: 10.1063/5.0061990
  45. Schreiner, M.; Bhowmik, A.; Vegge, T.; Busk, J.; Winther, O. Transition1x-a dataset for building generalizable reactive machine learning potentials. Scientific Data 2022, 9, 1, 779. DOI: 10.1038/s41597-022-01870-w
  46. Stuyver, T.; Jorner, K.; Coley, C. W. Reaction profiles for quantum chemistry-computed [3+ 2] cycloaddition reactions. Scientific Data 2023, 10, 1, 66. DOI: 10.1038/s41597-023-01977-8
  47. Spronk, S. A.; Glick, Z. L.; Metcalf, D. P.; Sherrill, C. D.; Cheney, D. L. A quantum chemical interaction energy dataset for accurately modeling protein-ligand interactions. Scientific Data 2023, 10, 1, 619. DOI: 10.1038/s41597-023-02443-1
  48. Khan, D.; Benali, A.; Kim, S. Y.; von Rudorff, G. F.; von Lilienfeld, O. A. Quantum mechanical dataset of 836k neutral closed shell molecules with upto 5 heavy atoms from CNOFSiPSClBr. arXiv preprint arXiv:2405.05961 2024. DOI: 10.48550/arXiv.2405.05961
  49. Ruddigkeit, L.; Van Deursen, R.; Blum, L. C.; Reymond, J. Enumeration of 166 billion organic small molecules in the chemical universe database GDB-17. Journal of Chemical Information and Modeling 2012, 52, 11, 2864–2875. DOI: 10.1021/ci300415d
  50. Sorokina, M.; Merseburger, P.; Rajan, K.; Yirik, M. A.; Steinbeck, C. COCONUT online: collection of open natural products database. Journal of Cheminformatics 2021, 13, 1, 2. DOI: 10.1186/s13321-020-00478-9
  51. Kaufman, B.; Williams, E. C.; Underkoffler, C.; Pederson, R.; Mardirossian, N.; Watson, I.; Parkhill, J. COATI: Multimodal contrastive pretraining for representing and traversing chemical space. Journal of Chemical Information and Modeling 2024, 64, 4, 1145–1157. DOI: 10.1021/acs.jcim.3c01753
  52. Riniker, S.; Landrum, G. A. Better informed distance geometry: using what we know to improve conformation generation. Journal of Chemical Information and Modeling 2015, 55, 12, 2562–2574. DOI: 10.1021/acs.jcim.5b00654
  53. Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-xTB—An accurate and broadly parametrized self-consistent tight-binding quantum chemical method with multipole electrostatics and density-dependent dispersion contributions. Journal of Chemical Theory and Computation 2019, 15, 3, 1652–1671. DOI: 10.1021/acs.jctc.8b01176
  54. Herr, J. E.; Yao, K.; McIntyre, R.; Toth, D. W.; Parkhill, J. Metadynamics for training neural network model chemistries: A competitive assessment. The Journal of Chemical Physics 2018, 148, 24.
  55. Gilmer, J.; Schoenholz, S. S.; Riley, P. F.; Vinyals, O.; Dahl, G. E. Neural message passing for quantum chemistry. International Conference on Machine Learning 2017, 1263–1272.
  56. Batatia, I.; Kovacs, D. P.; Simm, G.; Ortner, C.; Csányi, G. MACE: Higher order equivariant message passing neural networks for fast and accurate force fields. Advances in Neural Information Processing Systems 2022, 35, 11423–11436.
  57. Drautz, R. Atomic cluster expansion for accurate and transferable interatomic potentials. Physical Review B 2019, 99, 1, 014104.
  58. Falcon, W.; the PyTorch Lightning team. DOI: 10.5281/zenodo.3828935
  59. Yadan, O. Hydra - A framework for elegantly configuring complex applications. https://github.com/facebookresearch/hydra (accessed 2025-05-01).
  60. Weisfeiler, B.; Leman, A. The reduction of a graph to canonical form and the algebra which appears therein. Nauchno-Technicheskaya Informatsia 1968, 2, 9, 12–16.
  61. Hagberg, A. A.; Schult, D. A.; Swart, P. J. Exploring Network Structure, Dynamics, and Function using NetworkX. Proceedings of the 7th Python in Science Conference 2008, 11-15.
  62. Anstine, D.; Zubatyuk, R.; Isayev, O. AIMNet2: a neural network potential to meet your neutral, charged, organic, and elemental-organic needs. ChemRxiv preprint 10.26434/chemrxiv-2023-296ch 2023.
  63. Batatia, I. et al. A foundation model for atomistic materials chemistry. arXiv preprint arXiv:2401.00096 2023.
  64. Neumann, M.; Gin, J.; Rhodes, B.; Bennett, S.; Li, Z.; Choubisa, H.; Hussey, A.; Godwin, J. Orb: A fast, scalable neural network potential. arXiv preprint arXiv:2410.22570 2024.
  65. Rhodes, B.; Vandenhaute, S.; Šimkus, V.; Gin, J.; Godwin, J.; Duignan, T.; Neumann, M. Orb-v3: atomistic simulation at scale. arXiv preprint arXiv:2504.06231 2025.
  66. Kabylda, A.; Frank, J. T.; Dou, S. S.; Khabibrakhmanov, A.; Sandonas, L. M.; Unke, O. T.; Chmiela, S.; Müller, K.; Tkatchenko, A. Molecular simulations with a pretrained neural network and universal pairwise force fields. ChemRxiv preprint 10.26434/chemrxiv-2024-bdfr0-v2 2025.
  67. Barroso-Luque, L.; Shuaibi, M.; Fu, X.; Wood, B. M.; Dzamba, M.; Gao, M.; Rizvi, A.; Zitnick, C. L.; Ulissi, Z. W. Open Materials 2024 (OMat24) inorganic materials dataset and models. arXiv preprint arXiv:2410.12771 2024.
  68. Smith, D. G. et al. PSI4 1.4: Open-source software for high-throughput quantum chemistry. The Journal of Chemical Physics 2020, 152, 18. DOI: 10.1063/5.0006002
  69. Stratmann, R.; Scuseria, G. E.; Frisch, M. J. Achieving linear scaling in exchange-correlation density functional quadratures. Chemical Physics Letters 1996, 257, 3, 213-223. DOI: 10.1016/0009-2614(96)00600-8
  70. Add Fluorine to vDZP Basis Set (for wB97X-3c). https://github.com/psi4/psi4/issues/3205 (accessed 2025-05-01).
  71. Wang, L.-P.; Song, C. Geometry optimization made simple with translation and rotation coordinates. The Journal of Chemical Physics 2016, 144, 21, 214108. DOI: 10.1063/1.4952956
  72. Larsen, A. H. et al. The atomic simulation environment—a Python library for working with atoms. Journal of Physics: Condensed Matter 2017, 29, 27, 273002.
  73. Goerigk, L.; Hansen, A.; Bauer, C.; Ehrlich, S.; Najibi, A.; Grimme, S. A look at the density functional theory zoo with the advanced GMTKN55 database for general main group thermochemistry, kinetics and noncovalent interactions. Physical Chemistry Chemical Physics 2017, 19, 48, 32184–32215.
  74. Baker, J. Techniques for geometry optimization: A comparison of Cartesian and natural internal coordinates. Journal of Computational Chemistry 1993, 14, 9, 1085–1100.
  75. Zapata Trujillo, J. C.; McKemmish, L. K. VIBFREQ1295: A new database for vibrational frequency calculations. The Journal of Physical Chemistry A 2022, 126, 25, 4100–4122.
  76. Deng, B.; Choi, Y.; Zhong, P.; Riebesell, J.; Anand, S.; Li, Z.; Jun, K.; Persson, K. A.; Ceder, G. Overcoming systematic softening in universal machine learning interatomic potentials by fine-tuning. arXiv preprint arXiv:2405.07105 2024.
  77. Yuan, E. C.; Kumar, A.; Guan, X.; Hermes, E. D.; Rosen, A. S.; Zádor, J.; Head-Gordon, T.; Blau, S. M. Analytical ab initio hessian from a deep learning potential for transition state optimization. Nature Communications 2024, 15, 1, 8865.
  78. Risthaus, T.; Steinmetz, M.; Grimme, S. Implementation of nuclear gradients of range-separated hybrid density functionals and benchmarking on rotational constants for organic molecules. Journal of Computational Chemistry 2014, 35, 20, 1509-1516. DOI: 10.1002/jcc.23649
  79. Rodriguez, A.; Smith, J. S.; Mendoza-Cortes, J. L. Does Hessian Data Improve the Performance of Machine Learning Potentials?. arXiv preprint arXiv:2503.07839 2025.
  80. Karwounopoulos, J.; Bieniek, M.; Wu, Z.; Baskerville, A. L.; König, G.; Cossins, B. P.; Wood, G. P. F. Evaluation of Machine Learning/Molecular Mechanics End-State Corrections with Mechanical Embedding to Calculate Relative Protein–Ligand Binding Free Energies. Journal of Chemical Theory and Computation 2025, 21, 2, 967–977. DOI: 10.1021/acs.jctc.4c01427
  81. Rai, B. K.; Sresht, V.; Yang, Q.; Unwalla, R.; Tu, M.; Mathiowetz, A. M.; Bakken, G. A. Torsionnet: A deep neural network to rapidly predict small-molecule torsional energy profiles with the accuracy of quantum mechanics. Journal of Chemical Information and Modeling 2022, 62, 4, 785–800.
  82. Behara, P. K. et al. Benchmarking Quantum Mechanical Levels of Theory for Valence Parametrization in Force Fields. The Journal of Physical Chemistry B 2024, 128, 32, 7888–7902.
  83. Horton, J. T. et al. Open force field BespokeFit: automating bespoke torsion parametrization at scale. Journal of Chemical Information and Modeling 2022, 62, 22, 5622–5633.
  84. Ebejer, J.-P.; Morris, G. M.; Deane, C. M. Freely available conformer generation methods: how good are they?. Journal of Chemical Information and Modeling 2012, 52, 5, 1146–1158.
  85. Friedrich, N.-O.; de Bruyn Kops, C.; Flachsenberg, F.; Sommer, K.; Rarey, M.; Kirchmair, J. Benchmarking commercial conformer ensemble generators. Journal of Chemical Information and Modeling 2017, 57, 11, 2719–2728.
  86. McNutt, A. T.; Bisiriyu, F.; Song, S.; Vyas, A.; Hutchison, G. R.; Koes, D. R. Conformer generation for structure-based drug design: how many and how good?. Journal of Chemical Information and Modeling 2023, 63, 21, 6598–6607.
  87. Pracht, P. et al. CREST—A program for the exploration of low-energy molecular chemical space. The Journal of Chemical Physics 2024, 160, 11.
  88. Řezáč, J.; Bím, D.; Gutten, O.; Rulíšek, L. Toward accurate conformational energies of smaller peptides and medium-sized macrocycles: MPCONF196 benchmark energy data set. Journal of Chemical Theory and Computation 2018, 14, 3, 1254–1266.
  89. Appavoo, S. D.; Huh, S.; Diaz, D. B.; Yudin, A. K. Conformational Control of Macrocycles by Remote Structural Modification: Focus Review. Chemical Reviews 2019, 119, 17, 9724–9752.
  90. Diaz, D. B.; Appavoo, S. D.; Bogdanchikova, A. F.; Lebedev, Y.; McTiernan, T. J.; dos Passos Gomes, G.; Yudin, A. K. Illuminating the dark conformational space of macrocycles using dominant rotors. Nature Chemistry 2021, 13, 3, 218–225.
  91. Jain, A. N.; Brueckner, A. C.; Cleves, A. E.; Reibarkh, M.; Sherer, E. C. A distributional model of bound ligand conformational strain: from small molecules up to large peptidic macrocycles. Journal of Medicinal Chemistry 2023, 66, 3, 1955–1971.
  92. Poongavanam, V. et al. Conformational sampling of macrocyclic drugs in different environments: can we find the relevant conformations?. ACS Omega 2018, 3, 9, 11742–11757.
  93. Kim, T.; Baek, E.; Kim, J. Exploring Macrocyclic Chemical Space: Strategies and Technologies for Drug Discovery. Pharmaceuticals 2025, 18, 5, 617.
  94. Cleves, A. E. Obstacles and innovations of macrocyclic drug development. https://www.drugtargetreview.com/article/155484/obstacles-and-innovations-of-macrocyclic-drug-development (accessed 2025-05-01).
  95. Fu, X.; Wu, Z.; Wang, W.; Xie, T.; Keten, S.; Gomez-Bombarelli, R.; Jaakkola, T. Forces are not enough: Benchmark and critical evaluation for machine learning force fields with molecular simulations. arXiv preprint arXiv:2210.07237 2022. DOI: 10.48550/arXiv.2210.07237
  96. Fu, X.; Wood, B. M.; Barroso-Luque, L.; Levine, D. S.; Gao, M.; Dzamba, M.; Zitnick, C. L. Learning smooth and expressive interatomic potentials for physical property prediction. arXiv preprint arXiv:2502.12147 2025.
  97. Amin, I.; Raja, S.; Krishnapriyan, A. Towards Fast, Specialized Machine Learning Force Fields: Distilling Foundation Models via Energy Hessians. arXiv preprint arXiv:2501.09009 2025.
  98. Bigi, F.; Langer, M.; Ceriotti, M. The dark side of the forces: assessing non-conservative force models for atomistic machine learning. arXiv preprint arXiv:2412.11569 2024.
  99. Vanden-Eijnden, E.; Ciccotti, G. Second-order integrators for Langevin equations with holonomic constraints. Chemical Physics Letters 2006, 429, 1-3, 310–316. DOI: 10.1016/j.cplett.2006.07.086
  100. Wagen, C. Molecular and Periodic Calculations. https://rowansci.com/blog/molecular-vs-periodic (accessed 2025-05-01).
  101. Santra, G.; Martin, J. M. Some observations on the performance of the most recent exchange-correlation functionals for the large and chemically diverse GMTKN55 benchmark. AIP Conference Proceedings 2019, 2186, 1. DOI: 10.1063/1.5137915
  102. Santra, G.; Calinsky, R.; Martin, J. M. L. Benefits of Range-Separated Hybrid and Double-Hybrid Functionals for a Large and Diverse Data Set of Reaction Energies and Barrier Heights. The Journal of Physical Chemistry A 2022, 126, 32, 5492–5505. DOI: 10.1021/acs.jpca.2c03922
  103. Wang, Y.; Hait, D.; Unzueta, P. A.; Zhang, J. H.; Martìnez, T. J. Fast and Scalable GPU-Accelerated Quantum Chemistry for Periodic Systems with Gaussian Orbitals: Implementation and Hybrid Density Functional Theory Calculations. arXiv preprint arXiv:2410.22278 2024. DOI: 10.48550/arXiv.2410.22278
  104. Greenwell, C.; Beran, G. J. Inaccurate conformational energies still hinder crystal structure prediction in flexible organic molecules. Crystal Growth \& Design 2020, 20, 8, 4875–4881. DOI: 10.1021/acs.cgd.0c00676
  105. Zaverkin, V.; Holzmüller, D.; Schuldt, R.; Kästner, J. Predicting properties of periodic systems from cluster data: A case study of liquid water. The Journal of Chemical Physics 2022, 156, 11. DOI: 10.1063/5.0078983
  106. Daru, J.; Forbert, H.; Behler, J.; Marx, D. Coupled cluster molecular dynamics of condensed phase systems enabled by machine learning potentials: Liquid water benchmark. Physical Review Letters 2022, 129, 22, 226001. DOI: 10.1103/PhysRevLett.129.226001
  107. Reilly, A. M.; Tkatchenko, A. Understanding the role of vibrations, exact exchange, and many-body van der Waals interactions in the cohesive properties of molecular crystals. The Journal of Chemical Physics 2013, 139, 2.
  108. Dolgonos, G. A.; Hoja, J.; Boese, A. D. Revised values for the X23 benchmark set of molecular crystals. Physical Chemistry Chemical Physics 2019, 21, 44, 24333–24344. DOI: 10.1039/C9CP04488D
  109. Neumann, M. A.; van de Streek, J. How many ritonavir cases are there still out there?. Faraday Discussions 2018, 211, 441–458.
  110. Hunnisett, L. M. et al. The seventh blind test of crystal structure prediction: structure ranking methods. Structural Science 2024, 80, 6.
  111. Zhou, D. et al. A robust crystal structure prediction method to support small molecule drug development with large scale validation and blind study. Nature Communications 2025, 16, 1, 2210.
  112. Hoja, J.; Ko, H.; Neumann, M. A.; Car, R.; DiStasio Jr, R. A.; Tkatchenko, A. Reliable and practical computational description of molecular crystal polymorphs. Science Advances 2019, 5, 1, eaau3338.
  113. Slattery, S. A.; Yon, J. C.; Valeev, E. F. Revisiting artifacts of Kohn–Sham density functionals for biosimulation. Journal of Chemical Theory and Computation 2024, 110 20, 15, 6652–6660.
  114. Timofeev, V.; Chuprov-Netochin, R.; Samigina, V.; Bezuglov, V.; Miroshnikov, K.; Kuranova, I. X-ray investigation of gene-engineered human insulin crystallized from a solution containing polysialic acid. Structural Biology and Crystallization Communications 2010, 66, 3, 259–263.
  115. Bitzek, E.; Koskinen, P.; Gähler, F.; Moseler, M.; Gumbsch, P. Structural relaxation made simple. Physical Review Letters 2006, 97, 17, 170201.
  116. DiRocco, D. A. et al. A multifunctional catalyst that stereoselectively assembles prodrugs. Science 2017, 356, 6336, 426–430.
  117. Zubatyuk, R.; Smith, J. S.; Leszczynski, J.; Isayev, O. Accurate and transferable multitask prediction of chemical properties with an atoms-in-molecules neural network. Science Advances 2019, 5, 8, eaav6490.
  118. Katzberger, P.; Hauswirth, L. M.; Kuhn, A. S.; Landrum, G. A.; Riniker, S. Rapid Access to Small Molecule Conformational Ensembles in Organic Solvents Enabled by Graph Neural Network-Based Implicit Solvent Model. Journal of the American Chemical Society 2025.
  119. Explore various dataset generation strategies on simplified chemical space. https://github.com/openmm/spice-dataset/issues/89 (accessed 2025-05-01).
  120. Liao, Y.-L.; Wood, B.; Das, A.; Smidt, T. Equiformerv2: Improved equivariant transformer for scaling to higher-degree representations. arXiv preprint arXiv:2306.12059 2023.

Appendix: Hyperparameters

HyperparameterEgret-1Egret-1eEgret-1t
max_epochs190190190
batch_size128128128
val_split0.20.20.2
r_max666
atomic_inter_scale111
atomic_inter_shift000
num_bessel888
num_polynomial_cutoff555
max_ell333
num_interactions222
num_elements101110
num_channels192192192
max_L222
correlation333
gatesilusilusilu
pair_repulsionFalseFalseFalse
radial_typeBesselBesselBessel
distance_transformNoneNoneNone
learning_rate0.010.010.01
weight_decay5e-105e-105e-10
gradient_clip_val111
lr_scheduler_gamma0.990.990.99
lr_scheduler_patience202020
w_energy404040
w_forces100010001000
swaTrueTrueTrue
swa_lr0.000250.000250.00025
start_swa115115115
swa_w_energy100010001000
swa_w_forces101010
emaTrueTrueTrue
ema_decay0.99950.99950.9995
avg_num_neighbors22.91222.64220.033

Table 15: Hyperparameters for Egret-1 model variants.

ElementAtomic Energy (eV)
H−13.571965
C−1030.567165
N−1486.375026
O−2043.933693
F−2715.318529
Sia−7876.342032
P−9287.407133
S−10834.484471
Cl−12522.649269
Br−70045.283851
I−8105.734201

Table 16: Atomic-energy hyperparameters for Egret-1 models.
aOnly for Egret-1e.

Banner background image

What to Read Next

Modeling Thia-Michael Reactions

Modeling Thia-Michael Reactions

In which the addition of a thiolate to an enone proves to be unexpectedly difficult to model.
Jul 25, 2025 · Corin Wagen
API v2, New BDE Methods, MCP, And More

API v2, New BDE Methods, MCP, And More

new API philosophy; streamlined interfaces for workflows; using NNPs and g-xTB to predict bond strength; an MCP server; .sdf files; benchmarking protein–ligand interactions; Diels–Alder visualizations
Jul 21, 2025 · Spencer Schneider, Corin Wagen, Ari Wagen, Jonathon Vandezande, Ishaan Ganti, and Isaiah Sippel
ExpBDE54: A Slim Experimental Benchmark for Exploring the Pareto Frontier of Bond-Dissociation-Enthalpy-Prediction Methods

ExpBDE54: A Slim Experimental Benchmark for Exploring the Pareto Frontier of Bond-Dissociation-Enthalpy-Prediction Methods

ExpBDE54 is a benchmark dataset of experimental homolytic bond-dissociation enthalpies (BDEs) for 54 small molecules, used for benchmarking DFT, semiempirical methods, and NNPs.
Jul 17, 2025 · Jonathon E. Vandezande, Corin C. Wagen
Benchmarking Protein–Ligand Interaction Energy

Benchmarking Protein–Ligand Interaction Energy

How new low-cost computational methods perform on the PLA15 benchmark.
Jul 11, 2025 · Ishaan Ganti
Efficient Black-Box Prediction of Hydrogen-Bond-Donor and Acceptor Strength

Efficient Black-Box Prediction of Hydrogen-Bond-Donor and Acceptor Strength

Here, we report a robust black-box workflow for predicting site-specific hydrogen-bond basicity and acidity in organic molecules with minimal computational cost.
Jul 1, 2025 · Corin C. Wagen
Tracking Boltz-2 Benchmarks

Tracking Boltz-2 Benchmarks

Tracking the community's response to the new Boltz-2 model, plus some notes about Chai-2.
Jul 1, 2025 · Corin Wagen
g-xTB, Credit Usage, & More

g-xTB, Credit Usage, & More

the new g-xTB model from Grimme and co-workers; an easy visual overview of credit usage; better credit handling for organizations; bulk PDB download; a new collapsible JSON viewer
Jun 27, 2025 · Jonathon Vandezande, Ari Wagen, Spencer Schneider, and Corin Wagen
Representing Local Protein Environments With Atomistic Foundation Models

Representing Local Protein Environments With Atomistic Foundation Models

A guest post about how to use NNP embeddings for other prediction tasks.
Jun 20, 2025 · Meital Bojan and Sanketh Vedula
Co-Folding Updates

Co-Folding Updates

Boltz-2 FAQ and launch event recap; new visuals for co-folding workflows; new submission options; PDB bugfixes; new credit-management tools
Jun 12, 2025 · Ari Wagen, Spencer Schneider, and Corin Wagen
The Boltz-2 FAQ

The Boltz-2 FAQ

Questions and answers about the Boltz-2 biomolecular foundation model.
Jun 9, 2025 · Corin Wagen and Ari Wagen