Molecular and Periodic Calculations
by Corin Wagen · Nov 27, 2024
In computational chemistry, there are two types of calculations: molecular and periodic. This distinction is incredibly fundamental, but often underappreciated by people without deep computational experience. In this post, we'll examine the differences between molecular and periodic calculations and discuss when each sort of calculation is appropriate.
Molecular Calculations
Molecular calculations study finite molecular systems: isolated molecules or groups of molecules surrounded by a vacuum (or a dielectric field). This is good for studying small molecules, molecular clusters, or even larger biomolecules.
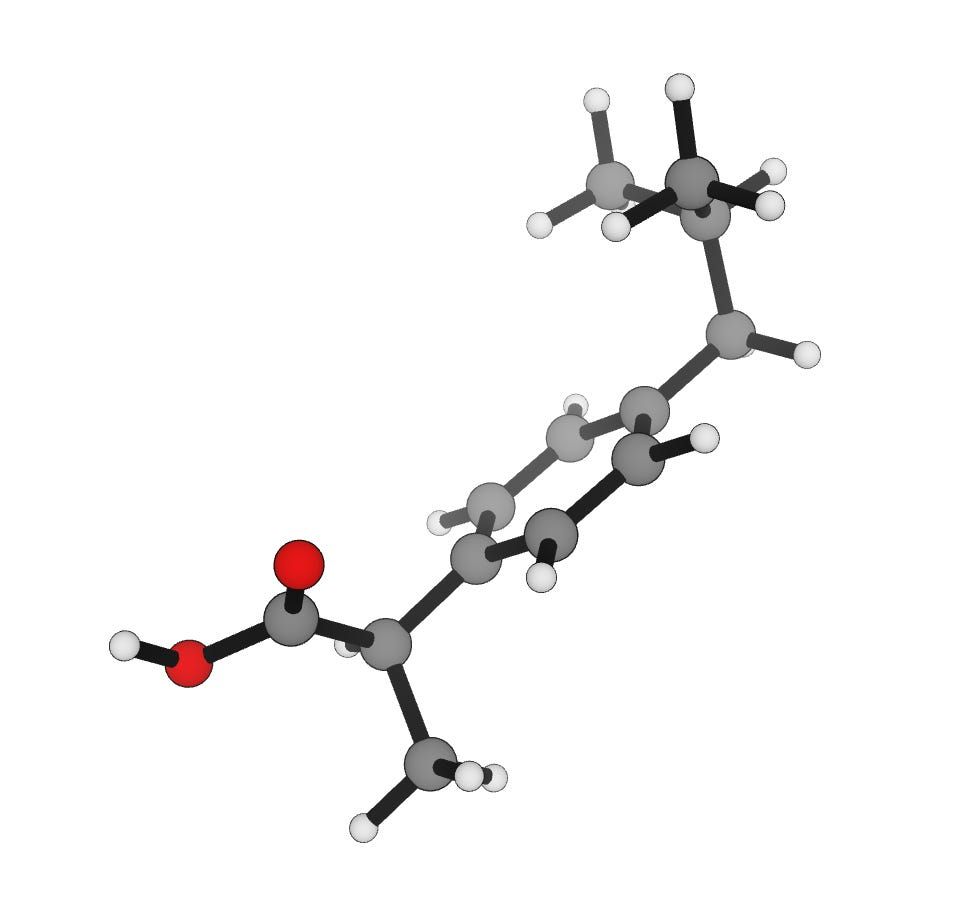
This molecule is surrounded by a vacuum.
Molecular calculations generally employ atom-centered real-space basis functions (like 6-31G(d), def2-TZVP, and so on). Since the systems under study are finite, a wide variety of advanced techniques can be used, like hybrid DFT functionals with long-range exact exchange or post-Hartree–Fock "gold standard" methods like coupled-cluster theory. It's possible to benchmark calculations in molecular systems with very high precision and rigorously approach or even exceed the accuracy of experimental values.
Most computational organic chemistry papers, like those exploring reaction mechanisms or homogenous catalyst design, employ molecular calculations. (Common programs like Gaussian, ORCA, TeraChem, Q-Chem, TURBOMOLE, and Psi4 almost always run molecular calculations.) This is possible because solvent effects can be modeled "implicitly" through solvent field methods like PCM, CPCM, and SMD, so there's no need to model vast numbers of solvent molecules.
Periodic Calculations
Molecular calculations are ill-suited to modeling continuous systems, like bulk liquids or solids: cutting out a chunk of these systems and modeling them with molecular calculations introduces significant edge effects. To solve this problem, we can use periodic calculations. Periodic calculations model infinite systems by using a repeating unit cell, where the molecule or group of molecules "sees" itself tiled infinitely in all dimensions.
For instance, here's a snapshot of seven periodic boxes of solid naphthalene. Where the molecule extends out of one side of the cell, it comes back on the other side:
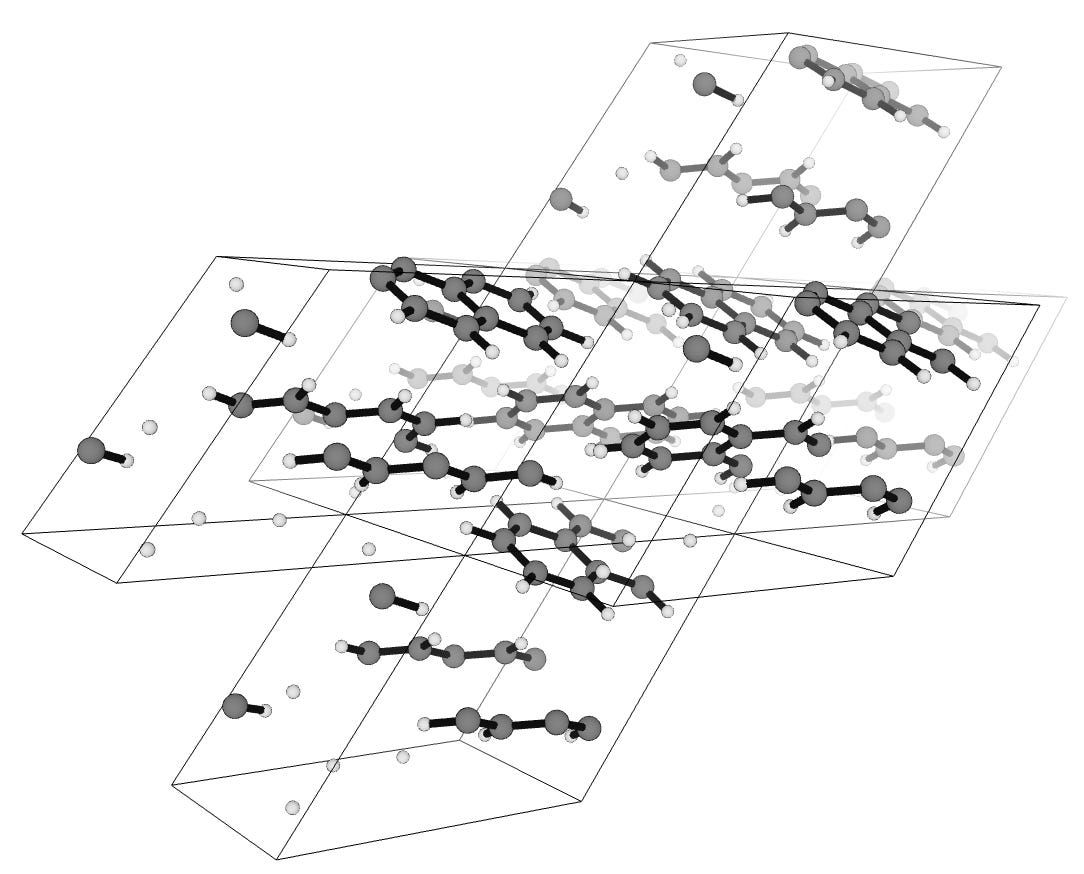
You can see that some atoms or molecules are "cut" by the unit cell boundaries; that's very normal. (You can view this calculation on Rowan.)
A wide suite of programs can be used to run periodic calculations, including VASP, Quantum ESPRESSO, FHI-aims, CP2K, and others. Most periodic DFT calculations employ plane-wave basis sets, although some periodic codes use atom-centered basis sets. This leads to a set of complex tradeoffs, which can be summarized in this excellent discussion. Most of the high-accuracy methods used in molecular DFT are unavailable to periodic DFT, making it considerably more challenging to benchmark periodic calculations in silico, and causing downstream inaccuracies in e.g. small molecule torsions.
Periodic calculations are great for a lot of tasks. To name just a few:
- Most crystals are inherently periodic, and periodic calculations allow direct study of the geometries, densities, and relative energies of different crystal structures. This is important in the pharmaceutical chemistry, where understanding the relative energetics of different crystal forms is crucial for ensuring reproducible and stable API crystallization. (Predicting crystal structures with DFT is also expensive. A recent crystal-structure-prediction competition saw 28 teams run over 46 million CPU-hours of computations!)
- Liquids have significant edge effects, so periodic calculations allow descriptions of liquid densities and dynamics. This is not only good for aqueous systems, like proteins and other biomolecules, but also solvent mixtures, battery electrolytes, melts, ionic liquids, and so on and so forth.
- Some reactions and processes are better described through periodic calculations. Heterogeneous catalysts are best modeled as an infinitely repeating surface on which a reaction takes place. Similarly, reactions in explicit solvent, phase transitions, or reactive polymerizations all require calculations that are devoid of edge effects.
Running Molecular and Periodic Calculations
As mentioned above, most tools in computational chemistry are intended for either periodic systems or molecular systems, not both. As a result, two largely separate ecosystems of researchers, software, and publications have emerged, and it's not uncommon for a given scientist to have extensive experience in molecular systems while never having run a periodic calculation.
However, recent advances in semiempirical methods and neural network potentials (NNPs) have made it possible to treat periodic and molecular calculations on the same footing. The xTB family of semi-empirical methods from Grimme and co-workers has full support for periodic systems, while graph-based NNPs like AIMNet2 and OMat24 can naturally work on both periodic and molecular systems. These methods are also orders of magnitude faster than conventional DFT methods, making them an appealing choice for rapid exploration or high-throughput in silico screening. For instance, this 250+ atom graphene system would take hours or days with DFT methods, but runs in only a few minutes with AIMNet2:
Rowan provides a unified interface for running both molecular and periodic calculations, making it simple to switch between different paradigms. Periodic cells will automatically be detected from input files as applicable, and these cells can be edited, added, or deleted to any structure in the Rowan platform. Both periodic and molecular optimizations can be conducted; Rowan will automatically adjust the optimizer and constraint schemas to make sure that calculations run as expected.