Quantum Chemistry in Drug Discovery

How it's used at present, and opportunities for the future.

Corin Wagen · Oct 12, 2023

Quantum chemistry—using quantum mechanics to model molecules and molecular processes—is a cornerstone of modern computational chemistry. This document aims to summarize the state-of-the-art of quantum chemistry, describe its existing applications to drug discovery, and imagine what the future of quantum chemistry for drug discovery might look like. The key conclusions are that (1) quantum chemistry is important to drug discovery and (2) improved quantum chemical software for drug discovery is surprisingly achievable.

1. Overview of Quantum Chemistry

What is quantum chemistry? We define it as the branch of science which attempts to apply quantum mechanics to the description of chemical systems. Quantum chemistry aims to construct detailed, physics-based models which accurately describe the structure, properties, and reactivity of molecules and molecular systems. Owing to the complexity of quantum mechanics and physics-based modeling, quantum chemistry has become almost exclusively a computational science, i.e. a science practiced through development and use of computer programs, although early quantum chemists didn't have this luxury.

In molecular simulation, a fundamental dichotomy exists between models employing quantum mechanics (i.e. quantum chemistry, also abbreviated “QM”) and models employing molecular mechanics (“MM”). MM methods (also known as “forcefields”) describe a molecule roughly like a series of balls and springs: each atom has a mass and a charge and each bond has a characteristic length and stiffness.¹1. You don't have to use a perfect Hooke's law energy expression, of course, and more complex polynomials are used.
(Additional parameters are used to describe the angular and torsional preferences of various bonds, and to account for non-bonding interactions.) Calculating forces and energies from a given list of coordinates mostly just requires evaluation of simple functions with the appropriate parameters; accordingly, MM is very fast and typically scales as O(NlnN).²2. This is of course a simplification: the most time-consuming part of most MM simulations is evaluation of long-range Coulombic interactions, which is typically not done naïvely (which would scale as O(N²)) but instead through an algorithm like particle mesh Ewald which decomposes the interaction into a near-field and far-field component.
The speed of MM allows thousands or tens of thousands of atoms to be simulated through molecular dynamics (MD) simulations, which frequently require a million or more individual calculations to achieve sufficient accuracy for the task at hand.³3. The length of simulation depends on the property under study, but the most common use of MD simulations in drug discovery is the study of (relative) binding affinity or protein conformational motion, for which timescales of 10–50 ns are commonly employed. (Longer timescales would certainly be helpful in many cases, but aren't easy to access.)

However, MM methods are fundamentally limited in important ways. Since they don't take electronic structure into account at all, they can't account for polarizability, changes in charge distribution, or changes in bonding.⁴4. Exceptions exist for all of these points, like TINKER and ReaxFF, but the claims in the text are true for the most common forcefields, like OPLS and GAFF.
Additionally, the functional forms and parameters typically employed are imperfect, leading to inaccurate conformations and energies. While accurate forcefields have been developed for relatively simple biopolymers, like proteins and nucleic acids, accuracy is much lower for arbitrary small molecules which may possess unusual structural features.⁵5. There are many interesting case studies of forcefields exhibiting dramatic failures in specific cases. A good general reference is this paper on the development of Schrodinger's OPLS4 forcefield, which highlights shortcomings of its predecessor OPLS3e across various regions of chemical space. One can safely assume that, as the bounds of “drug-like” chemical space evolve, OPLS4 will be found to have its own shortcomings.

Quantum chemical methods, in contrast, don't rely on user-specified bonding topologies and for the most part can faithfully reproduce the structure and reactivity of arbitrary molecules from only a list of atomic coordinates.⁶6. “High accuracy” is admittedly subjective, but we feel that this claim is broadly justified for most closed-shell organic molecules, solvation-related errors notwithstanding.
Their ability to describe the electronic structure of molecules enables them to predict a variety of physical and spectroscopic properties, and they typically show high accuracy across a range of benchmarks. The most significant limitation of QM methods is their speed: depending on the level of theory employed, calculations on 100–200 atoms can take days using state-of-the-art computers, making QM too slow for many applications. (To make matters worse, QM methods typically scale somewhere between O(N²) and O(N³)).⁷7. DFT and Hartree–Fock are often claimed to scale as O(N⁴) (sometimes O(N³) for non-hybrid DFT); as Johnson, Gill, and Pople point out in their landmark 1993 DFT paper, these claims are “strictly misleading” and assume “a naive implementation.” Linear scaling algorithms do exist for HF and DFT, but typical small molecules are too small to really reach the linear scaling regime, so we've gone with “O(N²)–O(N³)” in the text.

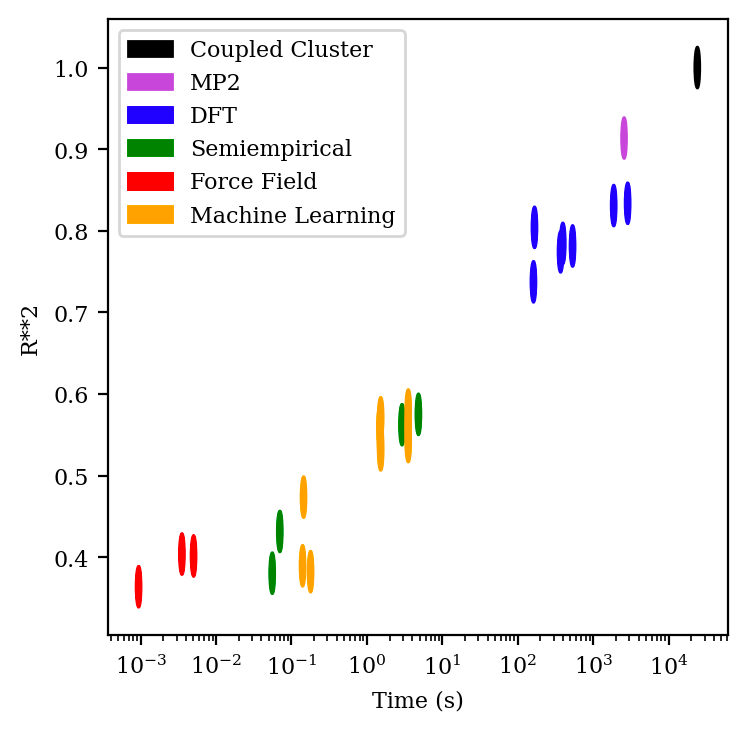
Figure 1. Speed–accuracy tradeoffs in computational chemistry: the x axis shows the mean time per calculation (in seconds), while the y axis shows the Pearson correlation coefficient of the resulting relative energy predictions. The width and height of the oval depict the standard deviation of the corresponding datum. Data from Dakota Folmsbee and Geoff Hutchinson; graph created by author.

This speed–accuracy tradeoff is vividly illustrated by data from Dakota Folmsbee and Geoff Hutchinson comparing the ability of different simulation methods to predict the relative energy of various conformations (Figure 1). The plot clearly illustrates a Pareto frontier, where MM methods (in red) and QM methods (in blue, purple, and black) possess different combinations of speed and accuracy. MM methods take fractions of a second to run but give very poor accuracy at conformational prediction, while QM methods take minutes or hours to run but give near-perfect accuracy. (The other methods depicted in Figure 1—semiempirical methods and machine learning—will be discussed later in this document.)

2. A Brief Introduction to how Quantum Chemistry Works

How does quantum chemistry work, and what makes it so slow and complicated? This section will attempt to summarize the key ideas behind quantum chemistry and introduce the necessary scientific concepts without alienating non-technical readers. Readers familiar with electronic structure theory (or those without any desire to become familiar with it) can safely skip this section.

At a high level, the complexity of quantum chemistry can be understood in analogy to the famous three-body problem from classical mechanics. The three-body problem studies a system of three particles, each possessing a mass, position, and velocity, which interact solely through long-range gravitational forces. This is a “problem” because, unlike the two-body case, there is no way to analytically predict the long-term behavior of the system: instead, expensive numerical simulations are required.

Quantum chemistry deals with very similar problems, but with a few important complications:

While the three-body problem has only three interacting bodies, molecules typically have hundreds or thousands of nuclei and electrons, all of which interact with one another through long-range Coulombic interactions.
Subatomic particles are delocalized (owing to wave–particle duality), so they can't be treated like point charges and must instead be modeled as probability densities. This makes evaluating interactions between them rather difficult.

Thus, exact numerical simulation of molecules is impossible for all but the smallest systems, and approximations are needed. The foundation of almost all quantum chemistry today is the Born–Oppenheimer approximation, which posits that the molecular wavefunction can be separated into the nuclear wavefunction and the electronic wavefunction. In colloquial terms, the timescale of nuclear motion is so much longer than the timescale of electronic motion that one can consider the nuclei as stationary with respect to the electrons.⁸8. There are plenty of important cases where this approximation is no longer valid, like electronic excited states or nuclear tunneling, but Born–Oppenheimer nevertheless reigns supreme for most applications.
The problem of quantum chemistry then becomes finding the lowest energy arrangement of electrons for a given arrangement of nuclei (the “electronic structure”). Practically speaking, this means that a quantum chemistry program accepts a list of elements and their positions and returns a description of the electronic structure of the molecule.

This problem is much more tractable, but is still very difficult, because each electron repels every other electron through Coulombic forces (“electron correlation”), and further approximations are needed. One foundational approach is the Hartree–Fock method (often abbreviated “HF”), which neglects specific electron–electron interactions and models each electron as instead interacting with the “mean field” exerted by the other electrons. Since the electronic mean field is itself a product of the position of the electrons, this becomes an iterative method: for a given electronic configuration, compute the mean field, and then compute the electronic configuration that this mean field gives rise to. For most systems, this “self-consistent field” (SCF) approach will yield a well-converged answer in 10–30 cycles.⁹9. It's worth noting, however, that SCF convergence is by no means guaranteed, and can be quite challenging in electronically complex systems (like many transition metals). There are intriguing parallels between SCF convergence and chaos theory explored here.

As discussed above, electrons are delocalized and reside in spatial distributions called orbitals. How are these orbitals described? For most applications, the desired “molecular orbitals” (MO) are constructed from linear combinations of atom-centered Gaussian spherical harmonics (“linear combination of atomic orbitals”, or LCAO for short). Selecting which atomic orbitals to employ for each atom (and how many) is difficult, and standard pre-optimized combinations of orbitals termed “basis sets” are typically used. Basis sets which contain the absolute minimum number of orbitals required for a given atom are called “single zeta” basis sets; basis sets which contain twice as many orbitals as needed are called “double zeta” basis sets, and so forth.

Use of the Hartree–Fock method requires computation of various integral quantities for each pair or quartet of basis functions, which are then used to construct matrices used to determine the energy of the system. The most demanding of the required integrals are the electron repulsion integrals (ERIs), which are evaluated over quartets of basis functions: for a molecule with 1000 basis functions, 1000⁴ = 10¹² ERIs must naïvely be evaluated.¹⁰10. In the late 20th century, a variety of algorithmic developments and insights in the computation and handling of ERIs led to a vast increase in the ability of quantum chemistry to describe medium-sized systems. For a good overview of how ERIs can be computed efficiently, see this review from Peter Gill; for an explanation of how a quantum chemistry program can be structured to scale to large molecules, see Almlöf, Fægri, and Korsell's landmark direct SCF paper.
Choice of basis set is thus an important consideration in the accuracy of a quantum chemical calculation; larger basis sets permit better resolution in describing electron distribution but require correspondingly more computational resources.

(So-called “semiempirical” methods eschew exact computation of these integral quantities, instead replacing them through heuristics and approximations determined by fitting experimental data. This makes them much faster, and less accurate, than full QM methods, as shown in Figure 1.)

The Hartree–Fock method's neglect of electron correlation leads to substantial errors (e.g. bonds that are too long and weak), and accordingly various ways to account for electron correlation have been developed. So-called “post-Hartree–Fock” wavefunction methods, like Møller–Plesset theory (cf. “MP2”, Figure 1) or coupled-cluster theory (cf. Figure 1) apply sophisticated physics-based corrections and achieve vastly improved accuracy, but at a much higher computational cost.¹¹11. Jack Simons has a good discussion of the requisite complexities here. Note that while there have been big advances in accelerating post-HF methods in recent years (e.g.), several factors still limit the broad applicability of these methods: (1) these algorithms require a huge amount of memory for even medium-sized molecules (on the order of 200 GB RAM per CPU core) and (2) for sufficient accuracy, post-HF methods generally require at least a triple-zeta basis set, whereas DFT can achieve adequate accuracy with a double-zeta basis set.

Probably the most widely used QM method today, however, is density-functional theory (DFT). Despite substantially different theoretical underpinnings than Hartree–Fock and related wavefunction theories, most implementations of DFT are nearly identical to Hartree–Fock, but with the addition of a “exchange–correlation potential” which approximates electron correlation as a function of the electron density and derivatives thereof. DFT is thus a mean-field method, like Hartree–Fock, and is much faster than post-HF methods while providing sufficient accuracy for most applications.¹²12. See, for instance, this benchmark from Stefan Grimme.

3. A Brief Introduction to how Computer-Assisted Drug Design Works

The central task of small-molecule drug design is multiparameter optimization over chemical space, as a drug molecule must balance many properties which are often anticorrelated with one another. Here are some of the most important:

Potency. The drug must have activity against its target—without this, nothing else matters.
Selectivity. There are many proteins in the body, and it's common for the target to be quite similar to innocuous proteins. Without selectivity for the desired target, off-target interactions can result, leading to decreased efficacy or even toxicity.
Bioavailability. The drug must actually be able to reach the intended target when administered. Ideally, the drug will be orally bioavailable, meaning it can be taken as a pill (although this isn't always possible). The drug must be able to enter into cells and, in the case of neurological targets, cross the blood–brain barrier.
Toxicity. The drug must not cause excessive toxicity. Of course, at sufficient doses every molecule can become toxic, but it's important that there's a “therapeutic window” where the drug can operate productively without excessive side-effects. (Certain functional groups frequently cause toxicity, like phenols, and thus are typically avoided.)
Metabolic Stability. The drug ought not to be metabolized too fast (or too slowly). This depends on the precise condition being treated and the desired properties of the drug.

Balancing these competing considerations is a complex task, made harder by the vast number of potential compounds (10⁶⁰ is generally considered a reasonable estimate). For a small-molecule drug, the process of preclinical drug development might, at a high level, look something like this:¹³13. For a great in-depth overview, see Austin et. al.’s “4DM map” (Nat. Rev. Drug Discov. 2018).

Target Identification. A biological target with disease relevance is identified and validated (e.g. a mutated protein that's driving cancer growth), and an assay for this target's activity is developed.
Hit Identification. A screening method is used to look through lots of potential drug-like molecules, and one or more molecules with some activity against the target are found. (High-throughput screening, DNA-encoded libraries, or virtual screening can all be employed here.)
Lead Optimization. The hit(s) found previously are modified, with the aim of finding a “lead candidate” with a good combination of properties. Potency is often the first variable optimized, but as the program advances the other properties above are also considered: rats or dogs can be used as model cases for bioavailability, toxicity, and pharmacokinetics, depending on the nature of the condition under study.
Candidate Selection. Based on all the data from the previous step, a clinical candidate is identified, and an IND application is filed to begin clinical trials.

While the bulk of the multi-billion dollar cost of bringing a drug to market resides in the clinical trial stage, the costs associated with the above steps are by no means trivial.¹⁴14. Some quantitative estimates can be found in the introduction to this paper: they estimate the total costs as $2 billion, and put preclinical costs at 43% of that. This suggests a rough figure of $840 million for all preclinical steps, of which the above workflow is a sizable fraction.
Over the past decades, molecular simulation has been used to substantially accelerate the steps shown above, with corresponding savings in time and money.

How does simulation help? For hit identification, virtual screening can be used in lieu of experimental screening methods: this is in theory an excellent use for computation, but in practice often yields underwhelming results, as the immense number of compounds under study limits the accuracy of the methods employed.¹⁵15. Derek Lowe has a number of nuanced posts on this topic: 1, 2, 3.
(Retrospective studies on virtual screening against COVID, for instance, have not been kind.) This is an active area of study, and significant further progress will doubtless be made (for instance, see this recent review from Gentile and co-workers.)

Perhaps the most common use of molecular modeling today, however, is in lead optimization, where the number of molecules under study is smaller and greater computational attention can be devoted to each one. One of the most common tasks is prediction of binding affinity through free energy methods, where the relative potency of different compounds against the target can be evaluated before synthesizing or purchasing any chemicals.¹⁶16. For a good overview, see this review from Cournia, Allen, and Sherman.
From a computational perspective, these methods typically involve relatively long molecular dynamics simulations, which makes them a good fit for forcefields. There are many other ways in which computational scientists can assist in lead optimization: constructing quantitative structure–activity relationship (QSAR) models, predicting metabolic sites, interpreting experimental spectral data, or designing new molecules with specific shapes or conformational preferences, to name just a few.

(It's worth noting here that many people outside of drug discovery seem to exhibit excessive computational optimism, bordering on naïvete—Derek Lowe has written about how many computational “breakthroughs” fail to address the actual rate-limiting steps in drug development. It's tempting to overreact and conclude that computation is a waste of time, but this is wrong: revealed preference demonstrates that computation is still valuable, even if it's only one piece among many.)

4. How Quantum Chemistry is Used in Drug Discovery

If quantum chemistry is too slow to predict binding affinities, how is it used in computer-assisted drug discovery (if at all)? We asked this question over a year ago, and spoke to about 50 scientists working in drug discovery in search of an answer. (My suspicion, before conducting these interviews, was that quantum chemistry had almost no practical uses outside academia.)

This suspicion was proven false. While quantum chemistry doesn't have a single big application to computer-assisted drug design (like FEP or docking), it finds use in plenty of ways, which we'll enumerate below:

Many small-molecule drugs are conformationally complex, and while MM methods can be used to generate conformational ensembles, they're not very good at scoring them (cf. Figure 1 again). Thus, conformations generated by MM programs are routinely reoptimized and scored by quantum chemistry. The output of these calculations can be used retrospectively to understand the orientation and shape of a successful compound, or prospectively to choose the starting coordinates for an MD simulation or identify compounds which fit into an active site in a new way.
Quantum chemistry is used to compute charges and electrostatic potentials for compounds, to help understand the physical origins of protein–ligand binding. This isn't necessarily a substitute for MD-based free energy calculations; rather, it's used in a supplemental way to build intuition.
Since off-the-shelf forcefields often struggle with arbitrary complex small molecules, it's becoming increasingly common to reparameterize forcefields for each compound under study. Quantum chemistry is used to generate the requisite data: this might involve charges, electrostatic potentials, torsional scans, and other calculations.
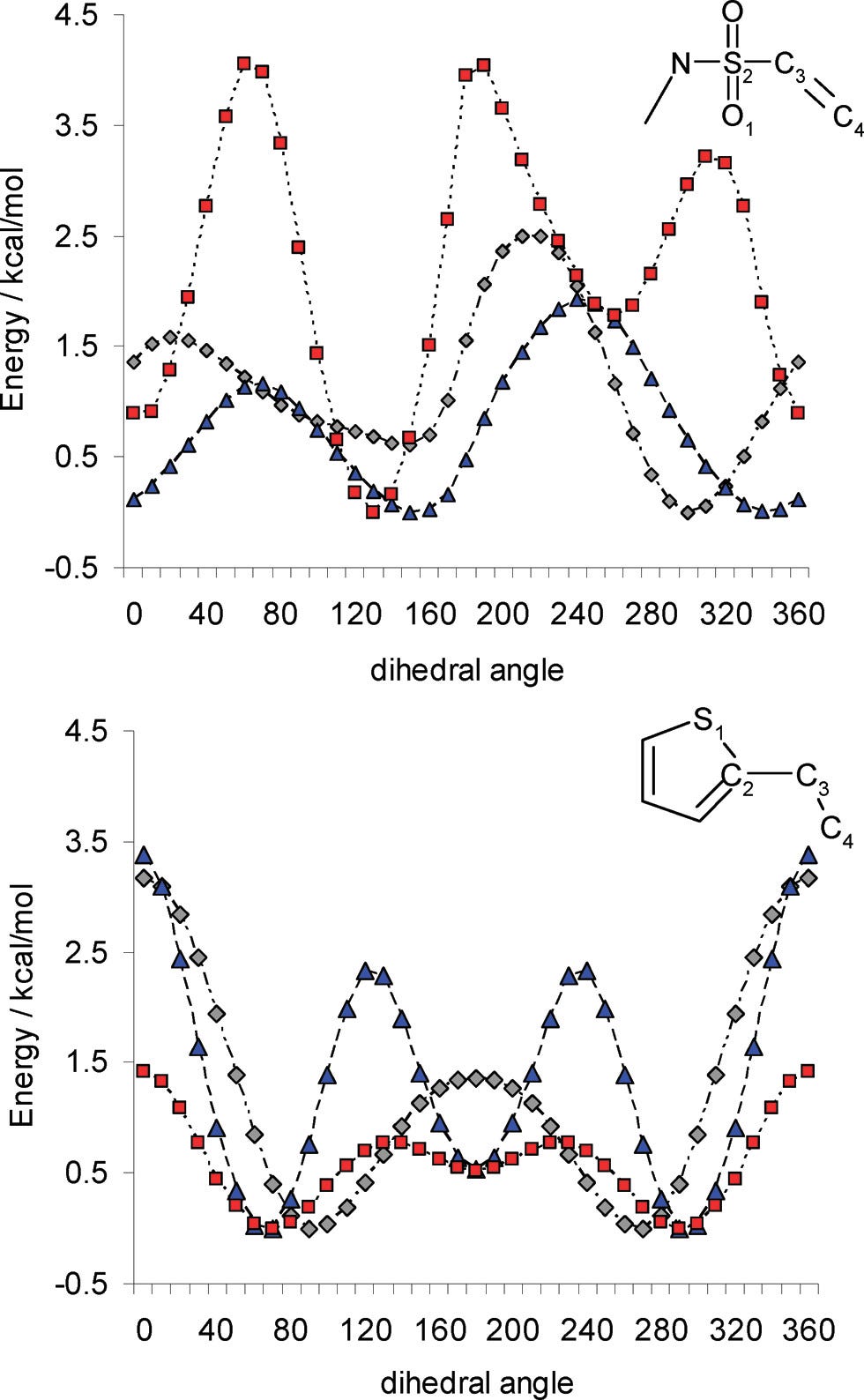
Figure 2. Illustrations of the difference between an accurate DFT torsional scan (red) and inaccurate MM torsional scans (OPLS in blue, MMFF in grey). From Gleeson and Gleeson, JCIM, 2009.
Similarly, torsional scans or ligand strain calculations can be done to understand unexpected increases or decreases in binding affinity across a series of ligands, or used prospectively to design a superior ligand without deleterious steric or conformational properties. One such case study from Roche is discussed here (see Figure 8).
Quantum chemistry is used to predict the pKa of various candidate molecules, which can be used to predict stronger binders. In particular, rapid evaluation of pKas across a library can be useful in “scaffold hop” scenarios, where a surrogate must be found for a previously conserved motif—in these cases, one can try to match important pKas and geometries between the different scaffolds as closely as possible.
Quantum chemistry is used to predict bond dissociation energies, which can be used to identify sites of potential metabolic instability. Since many metabolism pathways involve homolytic bond cleavage (e.g. CYP), the sites with the weakest bonds are often those which trigger metabolism first. (Metabolism is more complicated than just “weak bonds,” of course, so a QSAR/data science approach can be used in concert with QM calculations—a nice review can be found here.)
Many compounds can be found in multiple tautomers or protonation states, and identification of the correct tautomer/protonation state in the active site can be key to computing accurate binding affinities. (See this video for a detailed case study of how proper charge states can be crucial for correct MD simulations.)
Quantum chemistry can be used to model chemical reactivity and selectivity to assist process chemistry (the post-candidate selection step when a scalable route for compound manufacture is developed). Lam and co-authors from Merck Process have written a review highlighting uses of QM in process chemistry, which demonstrates how prospective calculations, e.g. on regiochemistry of aromatic substitution reactions, can help in route design. (The use of quantum chemistry in reaction design is a large topic which is too big to tackle here—as a starting point, the interested reader is referred to Mita and Schoenebeck's reviews on the topic.)
QM calculations are routinely used to model spectroscopic data to assist in experimental compound characterization. The most common forms of spectroscopy employed are NMR (for routine characterization) and vibrational circular dichroism (for determining absolute configurations of chiral molecules), although IR and UV-Vis also see use.
In the solid state, quantum chemistry is used to predict the relative stability of various crystal polymorphs, to inform scientists as they attempt to select a suitable formulation method. (This is a little different than the other applications; solid-state quantum chemistry requires periodic boundary conditions and plane-wave basis sets, not atom-centered basis sets, and as such typically employs different software packages.)
Covalent inhibitors, which react with their target to form a new chemical bond, are impossible to model with conventional forcefields, since the bonding of the system changes. Accordingly, QM calculations are needed to model the bond-forming process: either the entire system can be modeled in a multilayer scheme (e.g.), or bond formation can be studied in systems small enough to model entirely with QM.
Quantum chemistry is used to generate descriptors for QSAR studies, which use techniques from data science to predict various molecular properties. Quantum chemical descriptors include parameters like the ones discussed previously (pKa, charge, etc.) and a whole host of others.

Taken together, these applications differ in important ways from how quantum chemistry is used by academic researchers. Much more focus is placed on ground-state properties (relative energy of conformers, accurate prediction of torsional energy profiles, and property prediction), and prediction of barrier heights and reactivity—a cornerstone of academic applied computational chemistry—is correspondingly deemphasized.

Additionally, almost every application listed involves electronic ground states of high-bandgap organic molecules, the easiest molecules for quantum chemistry to handle. Many open problems in computational chemistry, such as accurate modeling of transition metals and other systems with substantial multireference or relativistic character, are completely avoided. Open-shell systems are almost completely ignored, with the exception of modeling bond dissociation energies.

Another surprising conclusion is that speed, not accuracy, is the main factor limiting the utility of quantum chemistry to pharmaceutical problems. Even relatively crude quantum chemical methods from an electron structure perspective, like DFT with double-zeta basis sets, are more than accurate enough for most of the applications listed above. At the margin, improvements in speed seem to be more important than improvements in accuracy.

(This implies that methods slightly faster and less accurate than DFT should be very popular. Unfortunately, quantum chemical methods are discrete, not continuous, and until recently few methods existed. While promising new methods have been reported in the last few years, broad adoption is inhibited by the limited availability of these methods.)

5. Characteristics of Existing Quantum Chemistry Software

Although over a hundred quantum chemistry packages exist, the industrial and academic markets are dominated by only a handful. The popularity of these packages among academics is monitored by the website atomistic.software, which publishes yearly rankings by citation count. While no such data exists for industrial usage, anecdotal evidence suggests that the rankings are similar.

By far the most popular software package is Gaussian, a venerable program dating back to the lab of Nobel laureate John Pople. The next most-used package is ORCA, which is under active development by the group of Frank Neese at Max Planck. Additional QC software packages include Molpro, GAMESS, TURBOMOLE, Q-Chem, NWChem, Jaguar, PySCF, Psi4, and MOLCAS (in order of popularity, excluding programs mainly used for other tasks which also have a quantum chemistry component).

There are considerable differences between these programs, both in terms of features and performance, but also many similarities. In particular, several important features are rare or non-existent. Almost all programs lack a working API, leaving users to parse giant text files by hand or with makeshift scripts, and only a handful of programs have any support for GPU-accelerated computing.

Furthermore, there is a need for quick incorporation of new advances. New algorithms are developed every year, but these algorithms find a home in (at most) one or two of the programs discussed above, leaving most scientists unable to take advantage of these discoveries. Among the important advances with limited availability are: occ-RI-K, a way to accelerate computation of two-electron integrals; r2-SCAN-3c, a lightweight “composite” DFT method that outperforms many more expensive methods; and wB97X-V, reportedly the one of the most accurate density functionals yet developed. Although these advances will no doubt trickle into most packages within the next handful of decades, the generally slow pace of academic software development leaves room for improvement.

6. Thoughts About the Future

Informed by the above considerations, what might the quantum chemistry software of the future look like? (This section is our opinion.)

As computing power becomes cheaper, calculations are increasingly run on ensembles, not single molecules: users want to see not just the ground state, but many different conformations, thermal perturbations, or analogues. Simultaneous consideration of many different structures is key to many of the applications listed above: conducting efficient virtual screens, performing accurate spectroscopic simulation, and determining complex reaction mechanisms. Accordingly, the chemistry software of the future ought to handle ensembles of structures naturally and efficiently. This will require improvements to both the user interface (making it easier to run and analyze calculations on ensembles) and the underlying software architecture (simple parallelization over different structures with minimal queue times). The massive on-demand CPU resources now available through cloud providers suggests that it should now be possible to run a thousand calculations in the same wallclock time it takes to run a single calculation.

Hardware heterogeneity also presents new challenges for quantum chemistry software. The plateau in single-CPU performance means that further speed improvements must come either from parallelization or use of specialized hardware like GPUs or TPUs. A recent perspective by Kowalski et al agrees:

While the homogeneity of CPU design has historically allowed for a certain level of hardware-software codesign in computational chemistry, particularly in its use of numerical linear algebra, it is clear that the dominance of graphics, artificial intelligence (AI), and machine learning (ML) will be the primary driver for specialized hardware innovation in the years to come. This paradigm shift is best represented by the introduction of accelerators, such as graphics processing units (GPU) and, more recently, AI-driven hardware such as tensor cores and tensor processing units (TPU), into the HPC ecosystem. In addition to a need for the development of novel programming models, compiler technologies, and optimized libraries to target these platforms, the move to accelerators often requires the re-evaluation of algorithmic design…

While a handful of quantum chemistry programs offer GPU support, like TeraChem and Psi4, in general it seems that broad adoption of these methods has not occurred, likely owing to the considerable technical challenges involved in adapting ERI evaluation to GPU architectures.¹⁷17. To my knowledge, no mainstream package yet offers TPU support, but there has been work showcasing the ability of TPUs to accelerate large-scale DFT.

From a design perspective, the “giant executable” model of quantum chemistry needs to be retired. New quantum chemistry programs ought to have simple Python APIs and integrate readily with multiple file formats and software packages, enabling easy workflow automation and scalability of protocols. The preponderance of competing software packages with different features means that multiple packages will likely be used in every workflow: even today it's not uncommon to start a task with molecular mechanics in RDKit, run intermediate semiempirical calculations in xtb, and finish with high-level calculations in Gaussian or ORCA. Interoperability and scripting will accordingly be key. (Kowalski et al make similar points here too.)

The user interface and user experience of computational chemistry will also need to evolve. Next-generation computational chemistry software should make it easier to generate, visualize, and export structural ensembles (either conformers or structural analogs), promoting best practices through its very design. As discussed above, new scientific advances also ought to be incorporated into software quickly and accurately, which suggests a non-academic approach to software development.

A unifying theme here is that many of the most needed short-term improvements to quantum chemistry require engineering advances, not scientific advances. As discussed above, the accuracy provided by existing levels of theory (e.g. DFT) seems sufficient for most current applications of quantum chemistry, and many of the improvements needed for pharmaceutical use cases require little to no scientific innovation. (Although, of course, pushing the Pareto frontier illustrated in Figure 1 outwards will always be important.)

A use for quantum chemistry that's rapidly growing in importance is generation of training data for machine learning. Existing machine-learned forcefields—both those trained on a whole set of compounds for broad usage, like ANI, and those intended to be trained anew for each molecule under study, like NequIP or atomic cluster expansion—rely on quantum chemistry, and particularly DFT, as a source of training data. Given that success in machine learning often relies on the use of massive training sets (e.g. the 13 trillion tokens used to train OpenAI's GPT4 model), it stands to reason that there will be a huge demand for quantum chemical data in the years to come. This application will require the same sorts of engineering advances mentioned above, namely easy parallelization across ensembles of structures, but on an even greater scale. (See also this review from von Lilienfeld which reaches a similar conclusion.)

What might more ambitious future uses of quantum chemistry be? The most obvious goal is QM-based prediction of binding affinities to biological targets. Quantum chemical accuracy can, in theory, mitigate the forcefield-induced errors which contribute to the less-than-perfect accuracy achieved by conventional free energy calculations (see e.g. this review by Schindler and Kuhn).

Unfortunately, this is very difficult; typical free energy perturbation calculations require around 10⁶–10⁷ individual calculations,¹⁸18. Alternative QM-based approaches to the problem of predicting binding affinities that rely on reduced sampling, like single point binding energies on protein–ligand complexes, seem like they will be poorly generalizable.
which means that each calculation must take about 50 milliseconds (or less) if a binding affinity is to be computed “overnight.”¹⁹19. 3600 s/hr * 10 hr for “overnight” / 10⁶ calculations = 0.036 s/calculation, rounded up in the text to 0.05 s = 50 ms to account for varying values of “overnight.”
It seems unlikely that quantum chemical methods will ever attain this speed for large systems like protein–ligand complexes. In their perspective on “Holy Grails” of computational chemistry, Liu and Houk agree:

We assume that even high accuracy DFT will always be too slow for billions of atoms problems that are at the heart of experimental chemistry. For example, even an invisible drop, like a micromole (∼10^–7 g) of water contains 10¹⁸ atoms! Classical force fields will be with us for a long time!

Accordingly, hybrid methods will be needed. Considerable success has been achieved with hybrid MM/ML methods employing neural networks trained with DFT data, suggesting that quantum chemistry can be used indirectly to assist in binding affinity prediction, if not directly. The problem of how best to integrate different levels of theory is a very challenging one, and it's likely that the next few years will see a huge amount of progress here. (One can imagine a tightly integrated QM-ML approach where training data is generated on the fly for unseen regions of chemical space, while faster ML calculations are run for regions with low uncertainty.)

Even more broadly, one can imagine fundamentally shifting the relationship between simulation and experiment in chemistry. In other fields, it's common for experimental practitioners to incorporate modeling into their workflow: designing a part, manufacturing it, testing it, and repeating this cycle a few times until the desired performance is achieved. This is currently more-or-less impossible in chemistry, but there's no fundamental reason why this should be the case. A powerful statement of this vision (albeit one more focused on “nanosystems” than drug design) can be found on the Astera Institute's page on molecular systems engineering:

Today, chemists have software to analyze small molecules and reactions in quantum detail, while protein and DNA nanostructure designers have specialized design tools, and other specialized tools exist for emerging molecular building blocks like spiroligomers. Non-quantum molecular dynamics simulations are possible but cumbersome to set up and don't readily support design. The barrier to entry is very large for people who would want to design and test, or simply envision, future molecular nano-systems, which would combine many of these elements in their functioning. We don't have anything analogous to AutoCAD or SolidWorks for “general” molecular systems engineering and atomically precise nano-machine design. Fortunately, making a much more general and useful molecular systems engineering CAD tool doesn't require any research breakthroughs, just good software engineering. (emphasis added)

What would it take to make chemical simulation software easy and robust enough for non-computational experts to use routinely? At a minimum, it means hiding unnecessary complexity and exposing only the necessary degrees of freedom to the end user, allowing them to make intelligent decisions without being experts on e.g. the minutiæ of SCF convergence parameters. But this vision also requires consideration of the “whole product”: what tasks scientists will want to perform, how they will set up their calculations, how data will be visualized and analyzed, how errors can be handled and detected automatically, and much more. Fortunately, as the text quoted above points out, these are ultimately hard, but not scientific, challenges, and thus can be overcome without the uncertainty of exploratory research.

There are many ways in which improved engineering and implementation can enhance the utility of QM software in the near future, and future scientific advances will doubtless help as well. Although quantum chemistry is still too slow for many key applications in drug discovery, the advent of machine-learned forcefields and the falling cost of computation suggests that the importance of high-accuracy quantum models will only increase in coming years. New software development, targeted at directly meeting the issues faced by pharmaceutical researchers, has the potential to make a big difference in this space.

Thanks to Ari Wagen for editing drafts of this piece, and to all the anonymous interviewees who contributed to Section 4. Any errors are mine alone.

You don't have to use a perfect Hooke's law energy expression, of course, and more complex polynomials are used.
This is of course a simplification: the most time-consuming part of most MM simulations is evaluation of long-range Coulombic interactions, which is typically not done naïvely (which would scale as O(N²)) but instead through an algorithm like particle mesh Ewald which decomposes the interaction into a near-field and far-field component.
The length of simulation depends on the property under study, but the most common use of MD simulations in drug discovery is the study of (relative) binding affinity or protein conformational motion, for which timescales of 10–50 ns are commonly employed. (Longer timescales would certainly be helpful in many cases, but aren't easy to access.)
Exceptions exist for all of these points, like TINKER and ReaxFF, but the claims in the text are true for the most common forcefields, like OPLS and GAFF.
There are many interesting case studies of forcefields exhibiting dramatic failures in specific cases. A good general reference is this paper on the development of Schrodinger's OPLS4 forcefield, which highlights shortcomings of its predecessor OPLS3e across various regions of chemical space. One can safely assume that, as the bounds of “drug-like” chemical space evolve, OPLS4 will be found to have its own shortcomings.
“High accuracy” is admittedly subjective, but we feel that this claim is broadly justified for most closed-shell organic molecules, solvation-related errors notwithstanding.
DFT and Hartree–Fock are often claimed to scale as O(N⁴) (sometimes O(N³) for non-hybrid DFT); as Johnson, Gill, and Pople point out in their landmark 1993 DFT paper, these claims are “strictly misleading” and assume “a naive implementation.” Linear scaling algorithms do exist for HF and DFT, but typical small molecules are too small to really reach the linear scaling regime, so we've gone with “O(N²)–O(N³)” in the text.
There are plenty of important cases where this approximation is no longer valid, like electronic excited states or nuclear tunneling, but Born–Oppenheimer nevertheless reigns supreme for most applications.
It's worth noting, however, that SCF convergence is by no means guaranteed, and can be quite challenging in electronically complex systems (like many transition metals). There are intriguing parallels between SCF convergence and chaos theory explored here.
In the late 20th century, a variety of algorithmic developments and insights in the computation and handling of ERIs led to a vast increase in the ability of quantum chemistry to describe medium-sized systems. For a good overview of how ERIs can be computed efficiently, see this review from Peter Gill; for an explanation of how a quantum chemistry program can be structured to scale to large molecules, see Almlöf, Fægri, and Korsell's landmark direct SCF paper.
Jack Simons has a good discussion of the requisite complexities here. Note that while there have been big advances in accelerating post-HF methods in recent years (e.g.), several factors still limit the broad applicability of these methods: (1) these algorithms require a huge amount of memory for even medium-sized molecules (on the order of 200 GB RAM per CPU core) and (2) for sufficient accuracy, post-HF methods generally require at least a triple-zeta basis set, whereas DFT can achieve adequate accuracy with a double-zeta basis set.
See, for instance, this benchmark from Stefan Grimme.
For a great in-depth overview, see Austin et. al.’s “4DM map” (Nat. Rev. Drug Discov. 2018).
Some quantitative estimates can be found in the introduction to this paper: they estimate the total costs as $2 billion, and put preclinical costs at 43% of that. This suggests a rough figure of $840 million for all preclinical steps, of which the above workflow is a sizable fraction.
Derek Lowe has a number of nuanced posts on this topic: 1, 2, 3.
For a good overview, see this review from Cournia, Allen, and Sherman.
To my knowledge, no mainstream package yet offers TPU support, but there has been work showcasing the ability of TPUs to accelerate large-scale DFT.
Alternative QM-based approaches to the problem of predicting binding affinities that rely on reduced sampling, like single point binding energies on protein–ligand complexes, seem like they will be poorly generalizable.
3600 s/hr * 10 hr for “overnight” / 10⁶ calculations = 0.036 s/calculation, rounded up in the text to 0.05 s = 50 ms to account for varying values of “overnight.”