Modeling Thia-Michael Reactions
by Corin Wagen · Jul 25, 2025
The addition of thiolates to α,β-unsaturated carbonyls (the "thia-Michael reaction") is an important reaction, not least because these conjugate acceptors are often used as electrophilic warheads for cysteine residues in covalent inhibitors (e.g. ibrutinib). Since modeling the reactivity of covalent warheads is one of the core uses of quantum chemistry in drug discovery, one might expect that commonly used density-functional-theory methods would be able to describe thia-Michael reactions with reasonable accuracy.
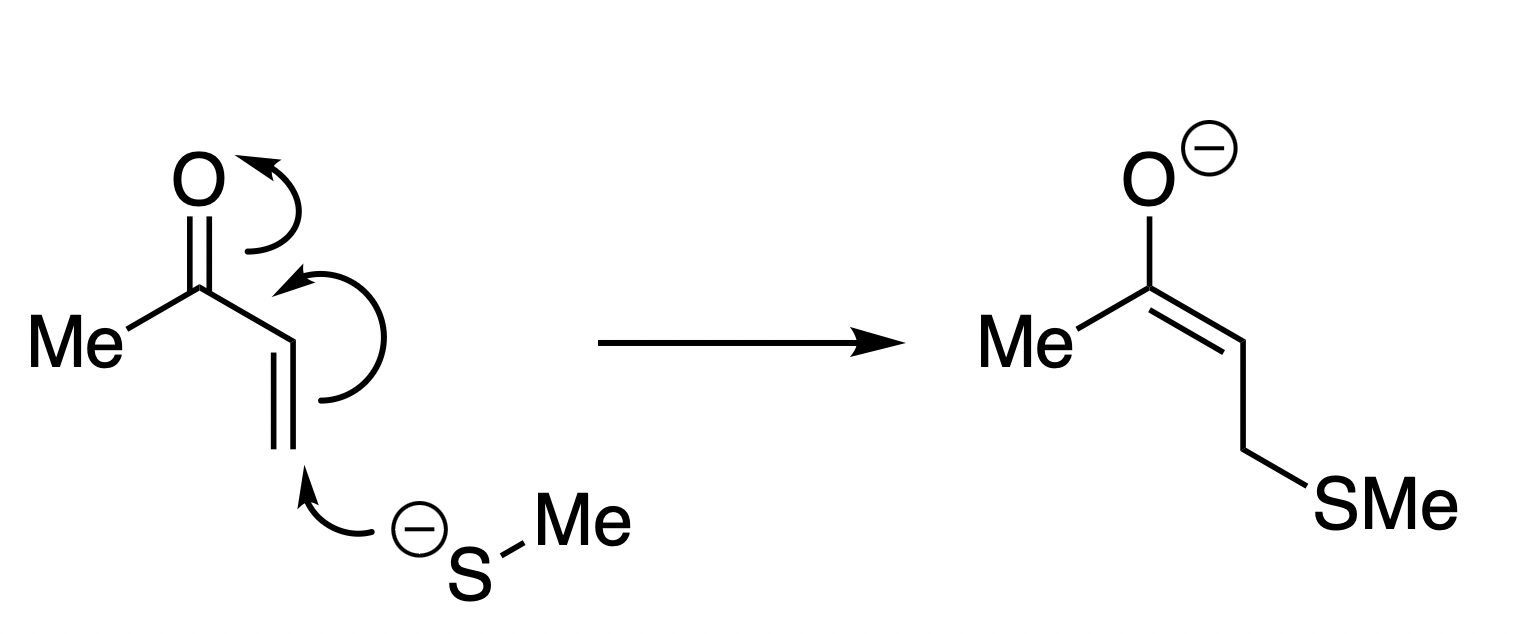
The thia-Michael reaction studied here.
This expectation is wrong. A fascinating 2013 article by Jennifer Smith, Yasaman Alahmadi, and Christopher Rowley demonstrates that many commonly used density functionals can't model this reaction. Only relatively sophisticated range-separated hybrids actually predict that the resulting enolate is a stable structure; methods without full exact exchange suffer from overdelocalization and predict that a charge-transfer complex will form instead. In the authors' words:
Functionals such as PBE and B3LYP favor long-range anion-to-π* charge transfer to reduce electron self-repulsion. This charge transfer distorts the potential energy surface to favor the noncovalent complex instead of the carbanion.
At Rowan, we're always interested in understanding how we can find practical low-cost solutions to useful scientific problems. We've been thinking a bit about covalent inhibition recently, so we decided to run a few tests on one of the systems that Smith et al studied here. Our goals were (1) to see if we can reproduce their results and (2) to understand how low-cost methods like semiempirical methods and neural network potentials fare here.
We started by comparing a few low-cost DFT methods: the ubiquitous workhorse, B3LYP-D3BJ/6-31G(d); the "Swiss-army-knife" pure functional, r2SCAN-3c; and the new composite range-separated-hybrid functional, ωB97X-3c. We chose methyl vinyl ketone and methanethiolate as our model system and ran a relaxed scan between the sulfur and the β carbon of the enone, scanning between 3.0 and 1.8 Å in 0.1 Å increments and using the wavefront propagation method to ensure that all scans were smooth and minimize hysteresis. Our results match what Smith et al report—only the range-separated hybrid ωB97X-3c correctly predicts that addition to the enone is (1) downhill and (2) produces a stable species.
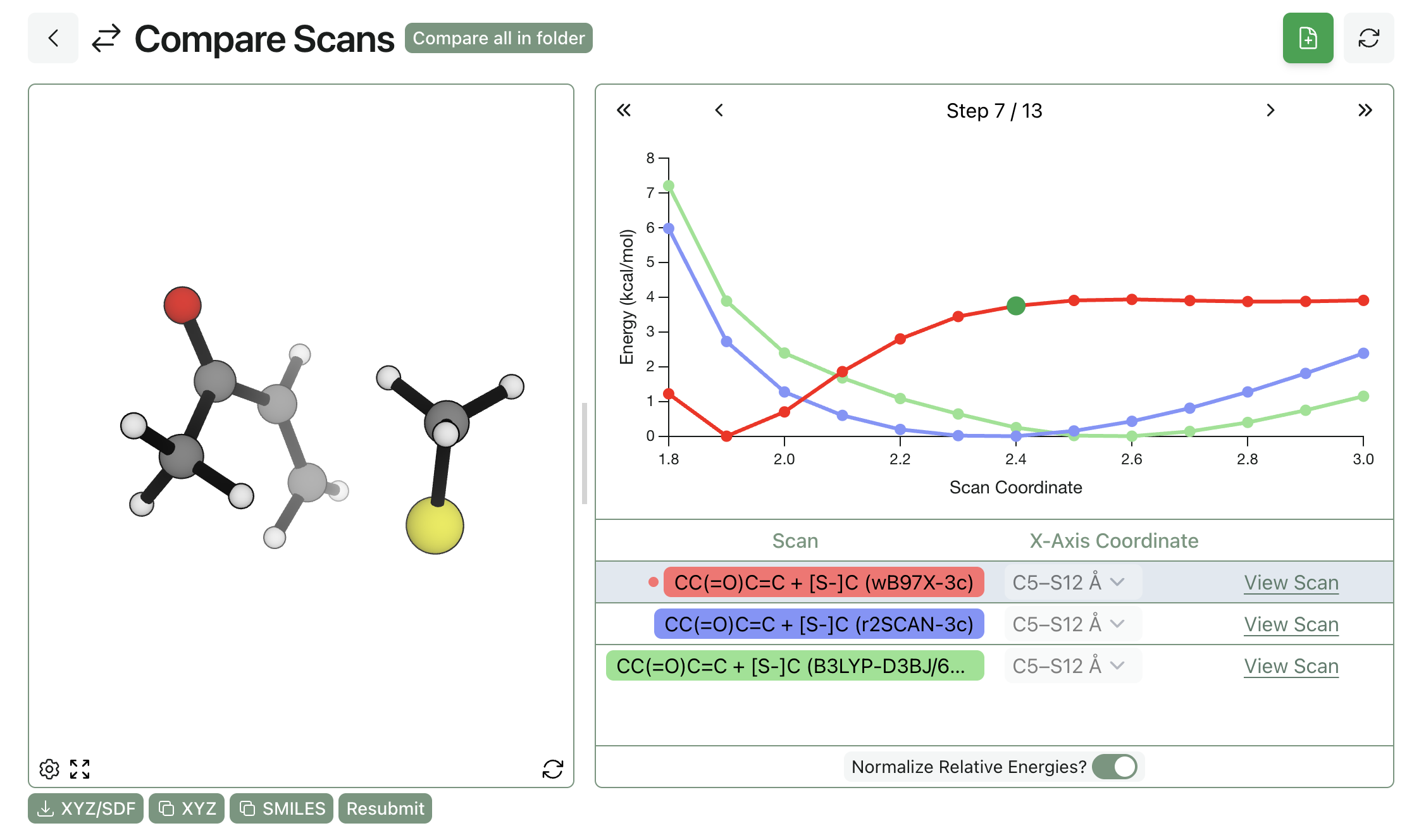
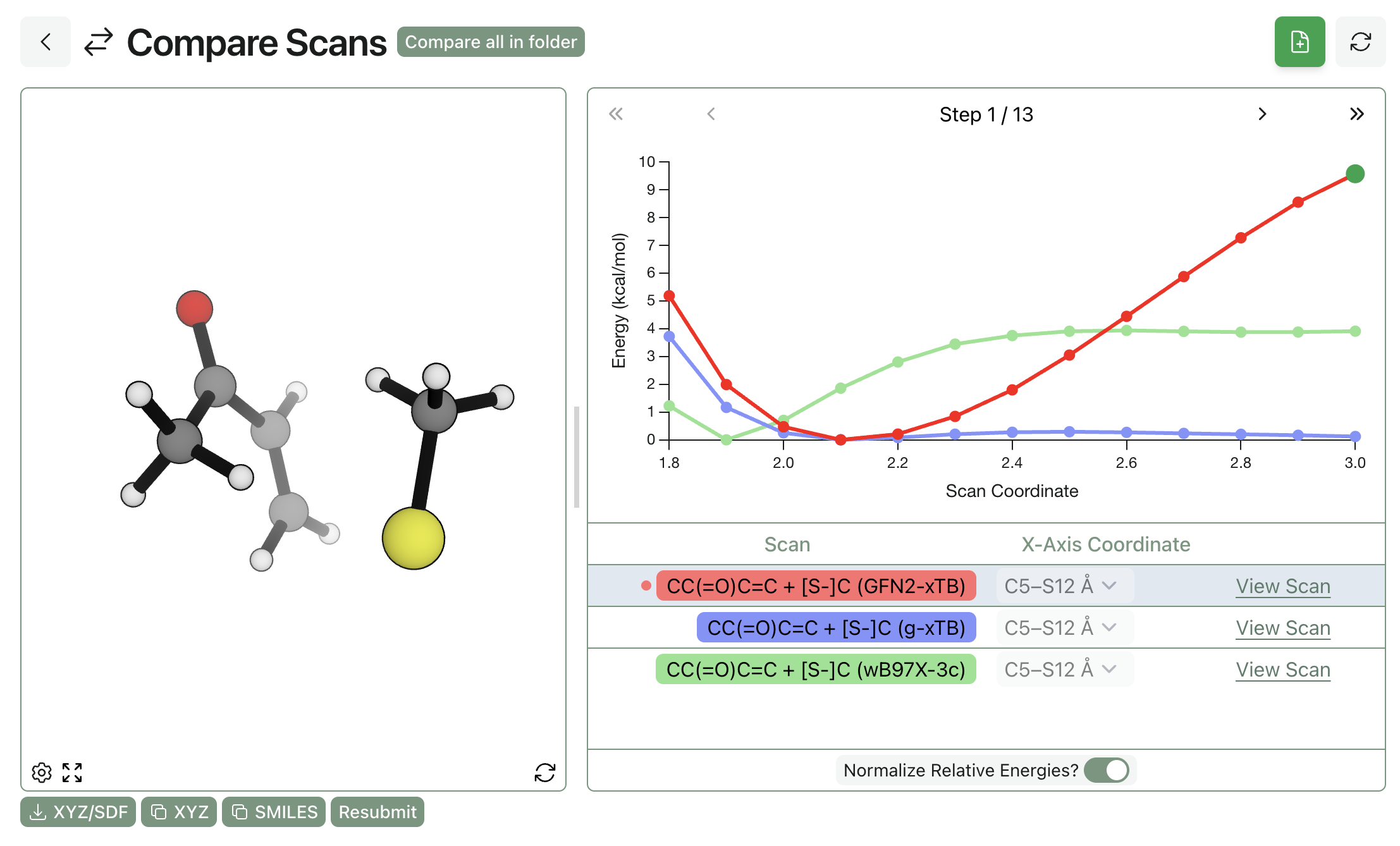
We next investigated the performance of two semiempirical methods: GFN2-xTB and g-xTB, both from Stefan Grimme and co-workers. We found that while g-xTB avoided the pathological charge-complex formation that occurred with r2SCAN-3c, the predicted enolate had an anomalously long C–S bond distance, and the overall reaction thermochemistry was wrong. GFN2-xTB predicts the reaction to be bombastically downhill but with the same incorrect minimum.
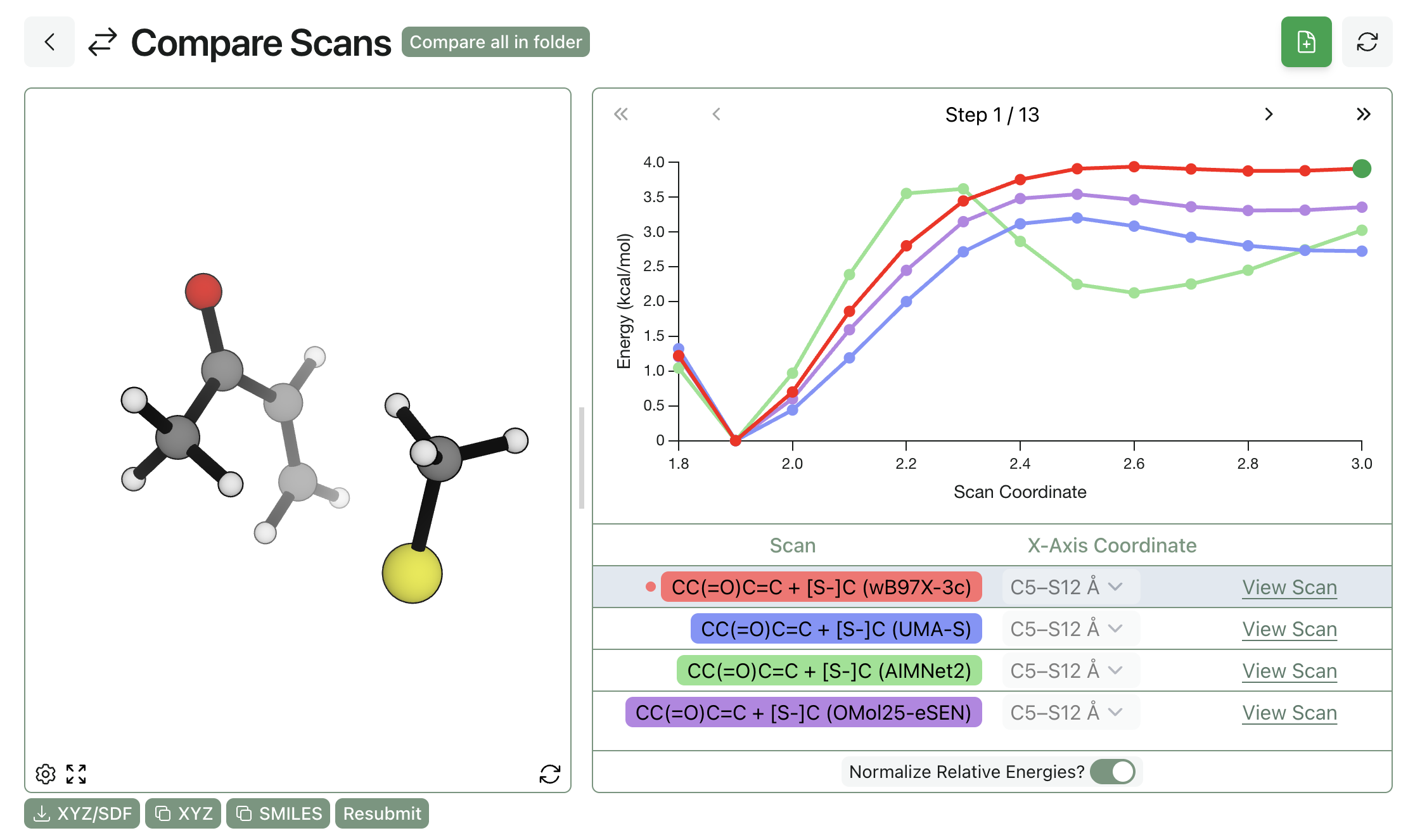
Finally, we looked at the performance of three new NNPs: AIMNet2, eSEN-OMol25-sm-conserving, and UMA-S. (The UMA-S model is the recent v1.1 release, not the original v1.0 release, although our tests indicate fairly small differences between the two versions.) We found that both eSEN-OMol25-sm-conserving and UMA-S give correct descriptions of the potential-energy surface, albeit with subtly different overall reaction thermochemistry—full benchmarking here would require a more detailed study. (This matches a lot of our other studies—the OMol25-based models seem very good across the board.)
AIMNet2 predicts a surprising pre-reactive complex at a C–S distance of approximately 2.6 Å and then a distinct barrier at around 2.2 Å: while this isn't as wrong as e.g. r2SCAN-3c or GFN2-xTB, it doesn't match the range-separated-hybrid calculations. (It's entirely plausible that AIMNet2-rxn fixes this, or the forthcoming new AIMNet2 release with improved electrostatics.)
This quick miniature study leaves many questions unanswered—how might this change in the presence of implicit solvent or other protein residues? Do larger basis sets make this better or worse? Which method's thermochemical predictions are most accurate? Nevertheless, I think these data demonstrate a few useful points.
First, the thia-Michael reaction is indeed a surprisingly challenging system even for modern computational methods. Some amount of care is needed to prevent bizarre phenomena from occurring in silico—while DFT experts might not be surprised by the delocalization errors seen here, I wouldn't have predicted this before reading the paper.
Second, good NNPs like the models trained on OMol25 can be an effective replacement for DFT calculations, and indeed give better accuracy than many of the quantum-chemical methods typically employed for such tasks. The NNPs are also much faster—the entire scan, including wavefront propagation, takes about two minutes using the eSEN-OMol25-sm-conserving model, whereas the ωB97X-3c scan takes almost two hours.
All the calculations run for this study can be viewed at this link. If you're interested in studying covalent inhibitors with modern computational methods, please reach out! We'd love to talk.