Common Errors in Density-Functional Theory
by Corin Wagen · Oct 15, 2024
Density-functional theory (DFT) calculations are a cornerstone of modern computational chemistry, but there are a lot of ways that they can go wrong. Here at Rowan, we often see calculations that have been run with suboptimal or unreliable settings, which makes it difficult to have confidence in the output results. Here are some of the most common and pernicious errors, and how we make sure they don't happen on our platform.
Grid Settings
DFT calculations evaluate the underlying density functional over a grid of points, and perform sums over the grid to obtain the final energy and gradients. "Denser" integration grids with more points per unit area are more accurate but also take more time to compute, while small integration grids are fast but yield unreliable answers.
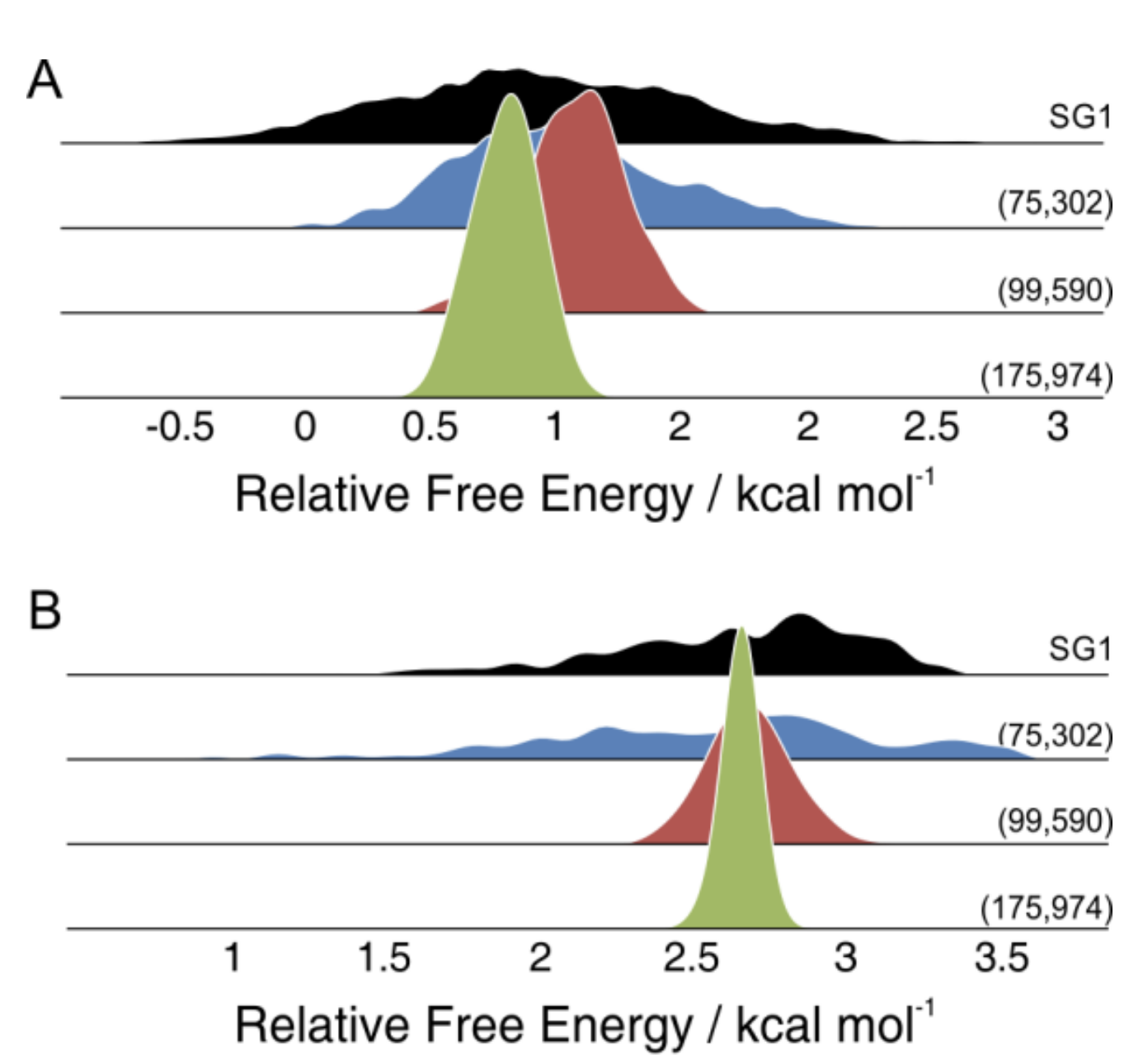
Integration grids typically have a radial component and an angular component, and the density of the grid is typically denoted by the combination of the two numbers. For instance, the "fine" grid in Gaussian is a (75,302) grid, meaning that there are 75 radial points * 302 angular points per radius = 22,650 points per atom. In practice, most integration grids are "pruned" to discard unimportant points, which typically reduces the size of the grid by 60–70%.
Relatively simple GGA functionals like B3LYP and PBE exhibit low grid sensitivity, meaning that small grids can safely be used. (The default in Q-Chem for a while was SG-1, a pruned (50,194) grid that showed good performance with these functionals.) Unfortunately more modern families of functionals, like mGGA functionals (e.g. M06, M06-2X) and many B97-based functionals (e.g. wB97X-V, wB97M-V), perform very poorly on these grids and require much larger grids. The SCAN family of functions, including r2SCAN and r2SCAN-3c, is particularly sensitive to these errors.
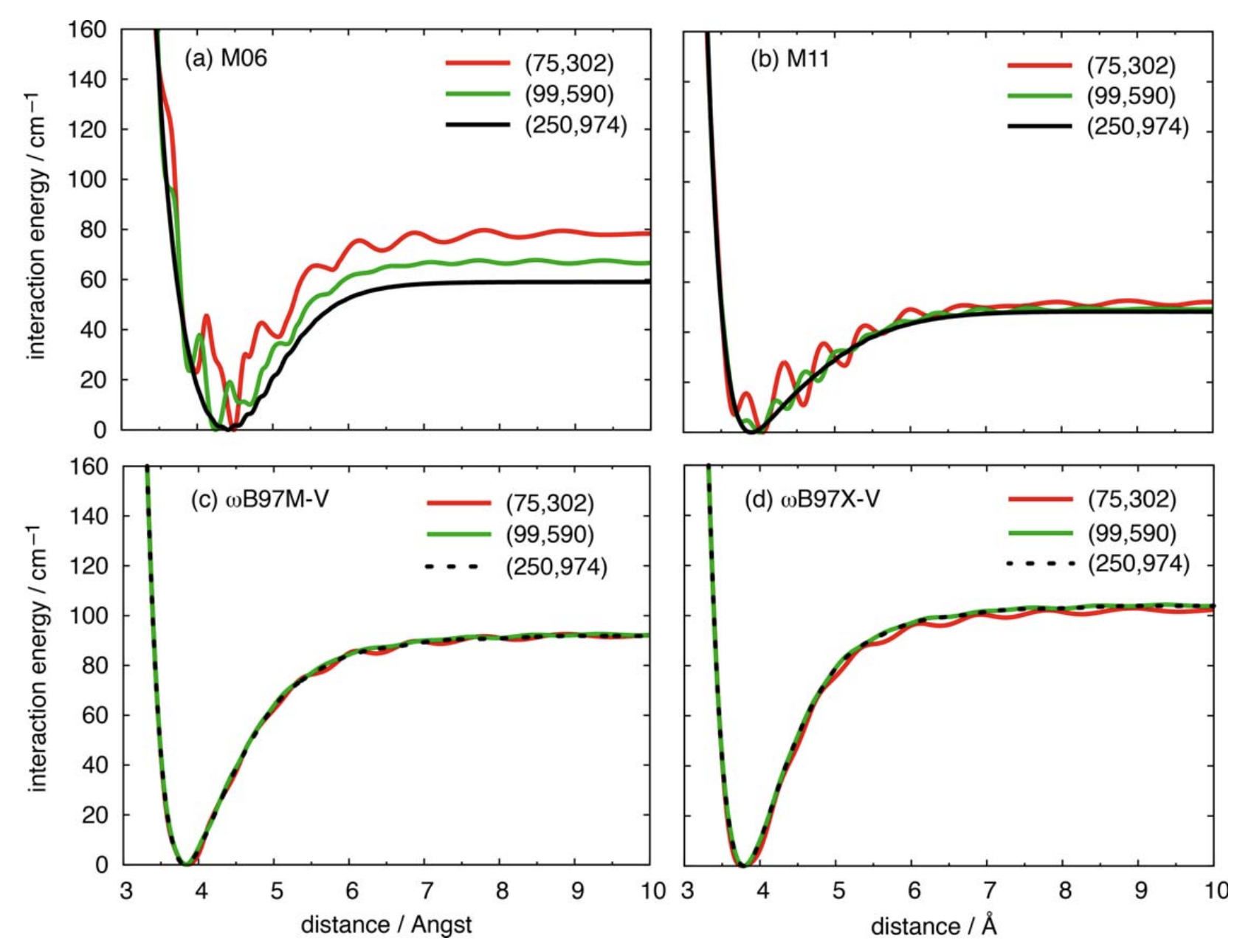
Slow DFT grid convergence for the Ar–Ar dimer. This is particularly bad for the Minnesota family of functionals, where even the largest grid evaluated doesn't fully eliminate the oscillations.
Furthermore, even functionals with low grid sensitivity for energies have recently been shown to exhibit much higher grid sensitivity for free energy calculations. A 2019 study by Andrea Bootsma and Steven Wheeler showed that even "grid-insensitive" functionals like B3LYP can exhibit surprisingly large variations in free energy depending on how the molecule is oriented: integration grids are not rotationally invariant, and so changing the exact pose of the molecule can lead to free energies that vary by 5 kcal/mol or more. These issues are dramatically reduced by using larger integration grids, and the authors recommend that no grids smaller than (99,590) should be used.
Small grids give dramatically different selectivity predictions based on the orientation of the molecule, and larger grids are needed to prevent this.
Today, it's generally accepted that a (99,590) grid should be used for almost all sorts of calculations, but many older computational chemistry programs still have smaller grids as the default. To help ensure that all answers are accurate and reproducible, Rowan automatically selects a pruned (99,590) grid for all DFT calculations (TeraChem has different grid specifications, so we select dftgrid 3, which is comparable).
Low Frequencies
Translations, rotations, and vibrations all contribute to the entropy of a system. Translations present a constant term based on the degrees of freedom (3 R/2 for a free molecule), rotations contribute inversely proportional to the rotational constants, and vibrations inversely proportional to the frequency of the vibration. This means that high-frequency vibrations (e.g. O–H stretches) contribute relatively little to the entropy of a system, whereas vibrational modes with small frequencies contribute much more.
Rowan automatically projects out translational and rotational modes from the Hessian matrix before computing the frequencies, and treats each type of mode separately. However, in some cases, the smallest vibrational modes also contain contributions from molecular rotation or translation (e.g. the "stretching" mode between two methanes at 10 Å apart, or the nearly unhindered rotation around an acetylenic group). These low-frequency modes can be due to incomplete optimization or be inherent to the system: in either case, treating them as vibrations can lead to an explosion in the entropic correction due to the inverse proportionality of the mode and the correction. Mookie Baik and co-workers have documented cases in which spurious low-frequency modes lead to incorrect prediction of reaction barriers or stereochemical outcomes.
To protect against cases where such low energy modes are present, Rowan applies the recommended Cramer–Truhlar correction, where all non-transition state modes below 100 cm–1 are raised to 100 cm–1 for the purpose of computing the entropic correction. This prevents quasi-translational or quasi-rotational modes from being incorrectly evaluated as anomalously low vibrational modes that lead to inaccurate entropy corrections in many literature results, and helps ensure that all free energies are as accurate as possible.
Symmetry Numbers in Entropy
One extremely common mistake in computational chemistry is to neglect the symmetry number of various species in a potential energy surface. High-symmetry species, like molecules with an axis of rotation, have fewer microstates. This lowers the entropy and can noticeably alter the thermochemistry of reactions that create or destroy a symmetry element.
Consider for example, the deprotonation of water: water is in the C2v point group and has a symmetry number of 2, while hydroxide is in the C∞v point group and has a symmetry number of 1. The overall ∆G0 must therefore be corrected by RTln(2), which at room temperature is 0.41 kcal/mol.
This effect is not always taken into account when computing thermochemistry, which leads to noticeable errors in the literature. Dan Singleton discusses this in the SI of his study of the Baylis–Hillman reaction:
For an entropy calculation to be properly compared with experimental observations, it should allow for a series of entropy effects that are not included in the entropies calculated from frequencies normally supplied by electronic structure calculations. This includes allowance for symmetry numbers and the effects of mixing of structures on entropy. The corrections are usually simple yet they are rarely done in computational mechanistic studies. A rationalization of this is that the effects are small and often make no difference for the results of greatest interest in papers. However, the effects can at times be quite large (see for example Seal, P.; Papajak, E.; Truhlar, D. G. J. Phys. Chem. Lett. 2012, 3, 264-271). Judging by papers where the consideration of symmetry numbers and entropy of mixing would make a difference but is ignored (for one example, see J. Chin. Chem. Soc. 2001, 48, 193-200), the ideas are not as widely recognized as needed.
Unlike the programs that Singleton discusses, Rowan automatically detects the point group and symmetry number of every species and applies the appropriate entropy correction, thus ensuring that computed values are maximally accurate. (We perform this analysis through the pymsym library, which we also maintain.)
SCF Convergence
Conventional electronic-structure-theory-based methods like DFT rely on a self-consistent-field (SCF) process, where an initial guess for the electron density is generated and then iteratively refined through repeated computation of electron–electron repulsion. This process frequently exhibits chaotic behavior, and SCF convergence can become extremely time-consuming or even impossible.
SCF convergence is a massive topic, and many different strategies can be employed: direct inversion in the iterative subspace (DIIS), augmented DIIS (ADIIS), tighter two-electron integral tolerances, level shifting, and so on. Rowan automatically employs all of these methods: we use a hybrid DIIS/ADIIS strategy where possible, apply a 0.1 Hartree level shift by default, and employ a tight integral tolerance (10–14). While these settings don't work for every system, we've found them to be very effective in our hands, and we rarely encounter cases where SCF convergence is difficult. (If this is happening with your system, reach out!)