Rowan

Physics-Informed Machine Learning Enables Rapid Macroscopic pKa Prediction

Corin C. Wagen
Apr 25, 2025
Accurate prediction of macroscopic pKa values remains a central challenge in computational chemistry, critical for modeling pH-dependent properties like solubility, membrane permeability, and charge state. Here we introduce Starling, a physics-informed neural network based on the Uni-pKa architecture trained to predict per-microstate free energies and compute macroscopic pKa values via thermodynamic ensemble modeling. Unlike approaches that treat protonation events in isolation, Starling explicitly resolves protonation and tautomeric microstates, enabling robust handling of complex molecules with multiple ionizable sites. We show that Starling achieves comparable or superior accuracy to leading commercial tools on multiple benchmark datasets, and demonstrate its utility in predicting isoelectric points, logD profiles, and blood–brain-barrier permeability. By maintaining thermodynamic consistency and enabling rapid microstate-ensemble generation, Starling enables accurate physicochemical property prediction with broad relevance to drug discovery and molecular design.

This preprint can also be viewed on ChemRxiv.

Introduction

The acid-dissociation constant (pKa) is a fundamental descriptor of molecular behavior in solution: it governs membrane permeability, solubility, charge distribution, and available reaction mechanisms. Accurate, rapid prediction of pKa values is critical to lead-optimization campaigns, physicochemical property modeling, and pH-dependent biophysical simulations.1,2

There are two complementary approaches to in silico pKa prediction. Microscopic models target single protonation events at specific atoms, allowing local rationalization of substituent effects, while macroscopic models describe the ensemble free-energy landscape spanning all protonation and tautomeric microstates (Figure 1).3,4 For properties governed by overall speciation at a given pH, macroscopic pKa prediction is indispensable—but exhaustive enumeration and weighting of all relevant microstates leads to a combinatorial explosion.

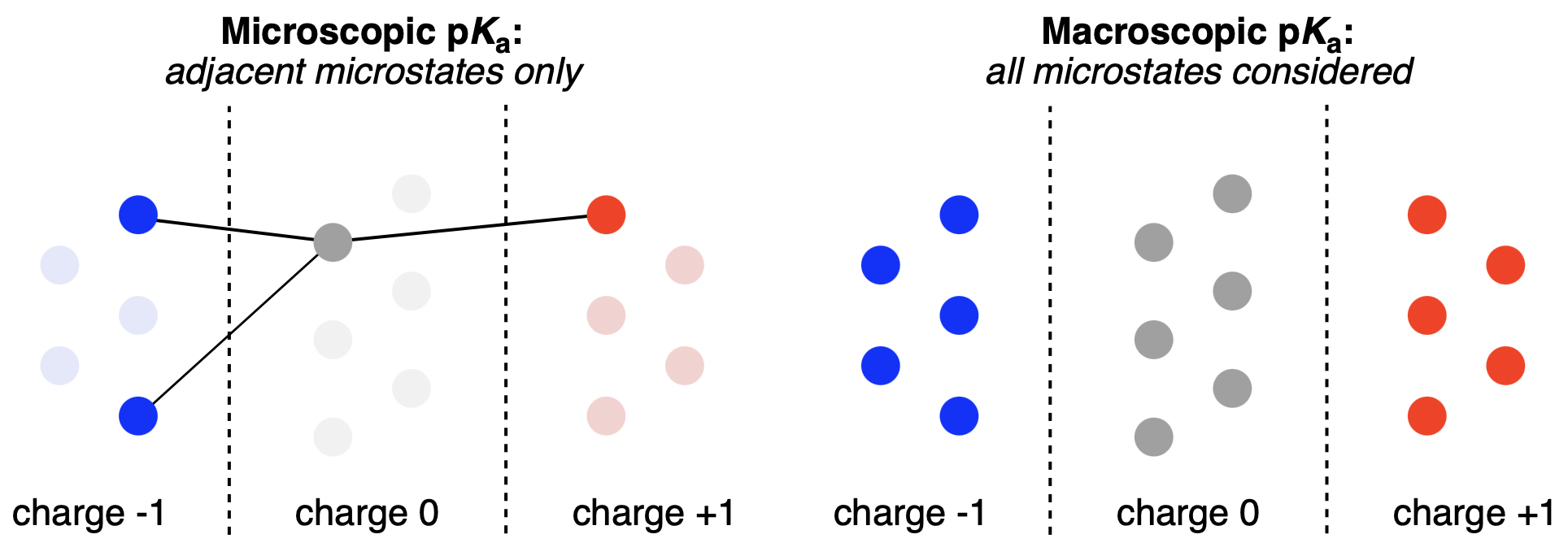
Figure 1: Macroscopic and microscopic pKa prediction strategies compared. Individual circles represent microstates.

Consequently, most open-source and commercial workflows employ the microscopic pKa paradigm, which breaks down in molecules with multiple, coupled protonation sites. Microscopic pKa methods often generate bizarre or invalid predictions in cases where multiple microstates are relevant, as highlighted by recent work from Jonathan Zheng, Ivo Leito, and William Green.3 In contrast, the recently reported Uni-pKa model from Weiliang Luo and co-workers satisfies thermodynamic constraints by learning per-microstate free-energy predictions that are combined into an overall macroscopic pKa.5 Zheng and co-workers specifically highlight the thermodynamic validity of this model in their article (emphasis added):3

Uni-pKa, published in 2024, also leverages the ChEMBL dataset to pretrain a module that leverages 3D information and computed free energies of individual microstates to calculate the overall macroscopic pKa. The model accounts for tautomerism, capturing the microscopic pKa of both the uncharged and zwitterionic tautomers. To our knowledge, this is the only recently released ML model that correctly distinguishes between those microstates.

While the original Uni-pKa paper focused on matching experimental pKa measurements on benchmark datasets, we hypothesized that the free energies generated by this physics-informed neural network might be gainfully employed in a variety of contexts. Here, we report Starling, a re-trained Uni-pKa model that retains state-of-the-art accuracy while accelerating inference relative to the original report. We integrate Starling into an end-to-end workflow that enumerates all potential microstates, predicts per-microstate free energies and populations, and uses these values to predict downstream properties like logD, isoelectric points, and unbound brain-to-plasma partition coefficient (Kp,uu).

Methods

Model Training

We retrained the Uni-pKa model of Luo and co-workers, introducing several modifications to improve inference speed and reduce training time. During the ChEMBL pretraining phase, we limited 3D conformer generation to three conformers per molecule (compared to ten in the original work), enabling dataset preprocessing to finish within several days. For fine-tuning on the Dwar-iBond dataset and test-time inference, the full ten-conformer set was used, as in the original Uni-pKa workflow. Training was conducted on a single NVIDIA H100 GPU via DigitalOcean.

For benchmarking, Luo and co-workers employed an ensemble of five models.5 In discussions on GitHub, Gengmo Zhou (one of the Uni-pKa authors) noted that "the five models are relatively large and not very convenient to use" and recommended using only a single fine-tuned model for inference.6 Following this advice, we employed only a single fine-tuned model for inference. The resulting model retained the same architecture and input format as Uni-pKa and is compatible with the original inference pipeline.

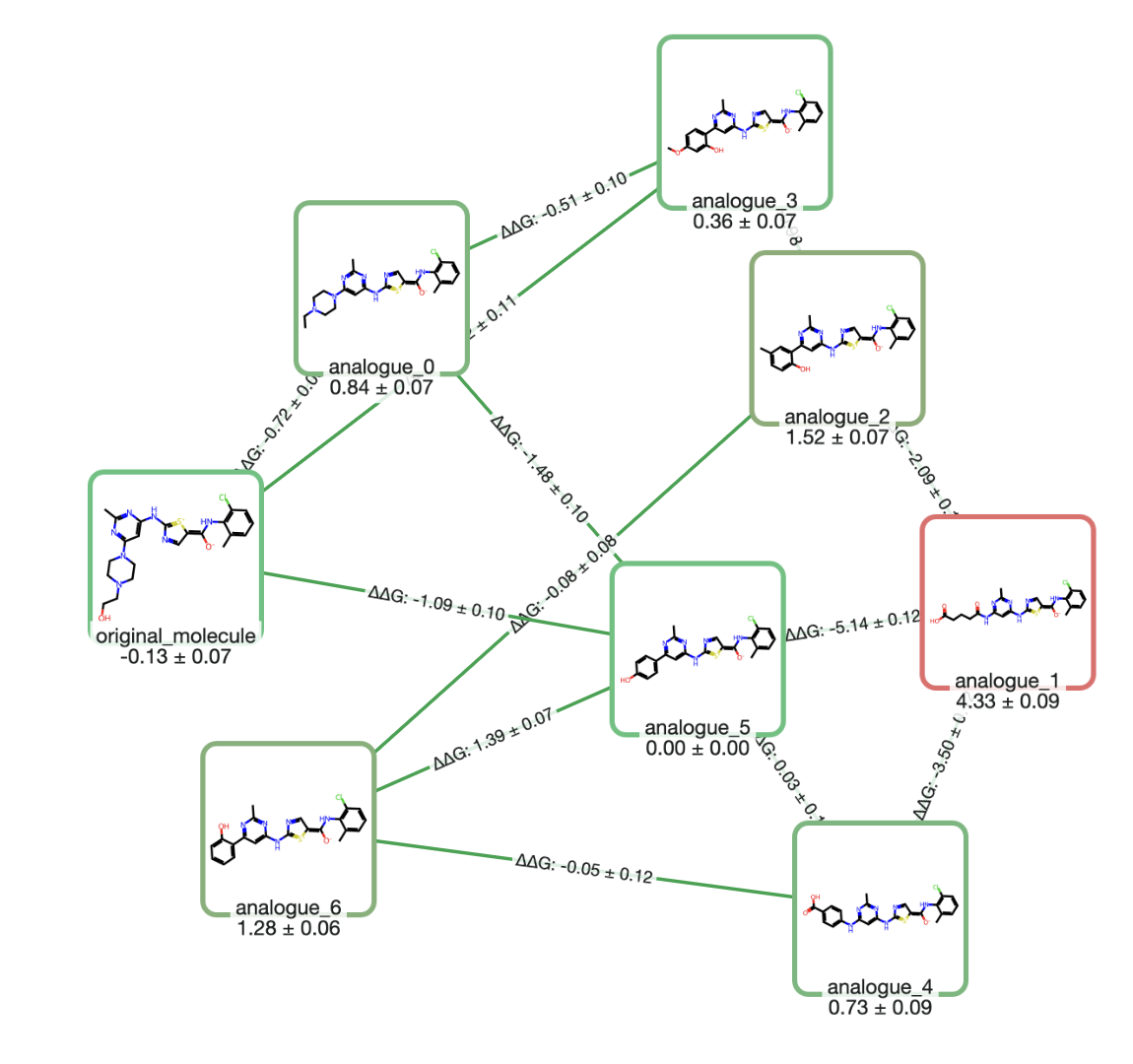
To enable subsequent comparison to the original Uni-pKa work (and disambiguate comments about the model from comments about the Uni-pKa architecture), the retrained Uni-pKa model will hereafter be referred to as "Starling" (Figure 2). Starlings are extremely social birds which often congregate in large flocks and engage in emergent behavior called ``murmuration," similar to how macroscopic pKa values emerge naturally from large numbers of microstates.

Figure 2: A common starling (Sturnus vulgaris), also known as a European starling in the United States.7

Microstate Enumeration

We employed a breadth-first-search (BFS) algorithm to enumerate protonation microstates within a formal charge window, by default [−2-2, +2+2]. Starting from the input molecule, we generated new microstates via formal charge edits using an RDKit-based substructure matching protocol.8 Atom-wise transformations were applied based on SMARTS patterns (adapted from the Uni-pKa data processing pipeline) and sanitized using RDKit's built-in sanitization routines.8

For each molecule, we applied both protonation and deprotonation transformations, iteratively exploring new states until all reachable microstates in the allowed charge range were visited. Chemically unreasonable structures (e.g. pentavalent carbon) were filtered out using a list of hard-coded substructure patterns (also from the Uni-pKa data processing pipeline). Each unique microstate was tracked using its canonical SMILES as an identifier.

We note that this approach does not account for the entropy of symmetry of individual microstates (e.g. monoprotonated diamines). Future work could apply an entropic correction to the free energy of each microstate based on its symmetry number, by analogy to conventional best practices in quantum chemistry.9 However, the low symmetry of most druglike molecules means that this inaccuracy will not impact most practical applications.

Free Energy Prediction

We used the Starling model to predict dimensionless free energies for each microstate. Conformers were generated via ETKDG10,11 and MMFF9412 optimization as implemented in RDKit.8 For each conformer, a feature representation was constructed using atom and formal charge tokenization, spatial distance matrices, and edge-type encoding, as required by the Uni-pKa architecture.

Predictions for each conformer were aggregated using a log-sum-exponential (LSE) procedure to yield a Boltzmann-averaged microstate energy:

Emicro=−log⁡∑iexp⁡(−Ei)E_\text{micro} = -\log \sum_i \exp(-E_i)

where EiE_i is the predicted energy of conformer ii.

Energies were further adjusted by adding a per-charge offset to account for the free energy of solvation of a proton. This offset, approximately −14.96-14.96 in model units, was inferred from the original Uni-pKa training data and computed as −6.50×ln⁡(10)-6.50 \times \ln(10), where −6.50-6.50 is the shift applied to the Uni-pKa model to align with experimental pKa data.

Macroscopic pKa Calculation

Macroscopic pKa values were computed by grouping microstates by formal charge and comparing free energies between adjacent charge states. For a charge transition c→c+1c \rightarrow c+1, the macroscopic pKa was computed using:

pKa=1ln⁡(10)[log⁡∑i∈c+1exp⁡(−Ei)−log⁡∑j∈cexp⁡(−Ej)]\text{p}K_\text{a} = \frac{1}{\ln(10)} \left[ \log \sum_{i \in c+1} \exp(-E_i) - \log \sum_{j \in c} \exp(-E_j) \right]

Microstate Populations and Derived Properties

By default, microstate populations were computed across pH 0–14 in 0.1 pH steps. The relative population wi(pH)w_i(\text{pH}) of microstate ii was calculated as:

wi(pH)=exp⁡(−Ei−qiln⁡(10)⋅pH)Z(pH)w_i(\text{pH}) = \frac{\exp(-E_i - q_i \ln(10) \cdot \text{pH})}{Z(\text{pH})}

where qiq_i is the charge of microstate ii and Z(pH)Z(\text{pH}) is the pH-dependent partition function.

logD Prediction: logD(pH) was calculated using weighted averaging of logP values in linear space:

log⁡D(pH)=log⁡10(∑iwi(pH)⋅10log⁡Pi)\log D(\text{pH}) = \log_{10} \left( \sum_i w_i(\text{pH}) \cdot 10^{\log P_i} \right)

logP values were computed using the Crippen logP function in RDKit for neutral species and set to −2-2 for ionic species.13 Proper handling of distribution coefficients for ionic species requires handling contact- and solvent-separated-ion pairs and becomes rather complex;14 based on previous reports,15 we found that simply employing a fixed logP of –2 for all non-neutral species gave results in good qualitative agreement with experiment. Since quantitative accuracy in the ionic limit is rarely needed in drug discovery, we expect this approximation to be suitable for routine use.

Isoelectric Point (pI): The average net charge across pH was computed, and the pI was defined as the pH where the net charge crossed zero, using bisection search with a convergence tolerance of 10−310^{-3}. If no sign change in net charge was detected across the pH range, the isoelectric point was omitted and a warning was logged.

Unbound Brain-to-Plasma Ratio Prediction

Following Morgan Lawrenz and co-workers at Schrödinger,16 we compute the aqueous solvation energy by comparing the electronic energies of conformer ensembles with and without solvent. The reported workflow takes up to 40 hours per molecule: to accelerate our implementation, we employ the AIMNet2 neural network potential from Dylan Anstine and co-workers to conduct geometry optimizations, and correct the optimized conformer energies using the CPCM-X implicit water model.17,18 Conformer ensembles are generated using the ETKDG algorithm as implemented in RDKit.8,10,11 Geometry optimizations were run using geomeTRIC 1.0.2.19

We generalize the Lawrenz state-penalty concept by directly computing the free-energy penalty associated with the molecule not being in a chemically neutral, non-zwitterionic form at physiological pH. Specifically, we evaluate the Boltzmann-weighted population of microstates that are formally neutral and minimize atom-centered charges—preferring, for example, the glycine microstate with a neutral backbone (i.e., protonated carboxylic acid and deprotonated amine) over its zwitterionic counterpart. When no fully neutral form exists, we select the microstate with the fewest formal atom-centered charges. The state penalty is then defined as the free energy required to shift the ionization equilibrium toward this reference state:

SP:=−RT⋅ln⁡(∑i∈neutral pi)\text{SP} := -RT \cdot \ln \left( \sum_{i \in \text{neutral }} p_i \right)

where pip_i is the population of neutral microstates at pH 7.4. This approach accounts for multiple protonation sites, tautomerism, and protonation-coupled conformational changes, and it avoids the need to heuristically assign a single dominant pKa or ionizable group.

To compare the predictive efficacy of the Schrödinger-reported solvation energy to our AIMNet2/CPCM-X(water)/Starling solvation energy, we binarized log-transformed Kp,uu values at 0.3 to define a "brain-penetrant" class, trained logistic-regression models using both descriptors, and assessed model performance by 5-fold stratified cross validation and receiver operating characteristic (ROC).

Results and Discussion

pKa Prediction

Our focus here is on pragmatic physics-informed macroscopic pKa modeling that can be deployed in a variety of tasks, not in maximizing benchmark accuracy. Towards this end, we reduced the size of the parent Uni-pKa model by employing only a single model and not an ensemble of five models, following the authors' advice.6 The resultant Starling model is small enough to easily run inference on CPU-only machines, dramatically simplifying usage and deployment.

To assess the impact of this change on overall pKa-prediction accuracy, we compared our Starling model to a wide variety of pKa-prediction models: the original Uni-pKa model,5 the MolGpka graph-convolutional model from Xiaolin Pan and co-workers,20 ChemAxon's commercial Marvin pKa plugin, Schrödingers commercial Epik Classic and Epik 7 models,21,22 and the QupKake model from Omri Abarbanel and Geoff Hutchison.23 Following the original Uni-pKa publication, we benchmarked Starling on the Czodrowski Novartis dataset and the SAMPL6, SAMPL7, and SAMPL8 pKa-prediction challenges (Table 1).4,24,25,26

MethodNovartis BaseNovartis AcidSAMPL6SAMPL7SAMPL8
Uni-pKa0.6531.0610.7160.7350.878
MolGpka1.0641.2870.7730.9801.150
ChemAxon Marvin1.1451.1441.2480.7081.511
Epik Classic1.1751.5310.9621.648---
Epik 7 (ensemble)------0.61------
QupKake------0.440.851.04
Starling0.7971.1091.1020.7461.141

Table 1: Root-mean-squared error of pKa predictions by benchmark set. Blank entries denote benchmarks for which data is not available. All results taken from the SI of the Uni-pKa manuscript5 except for Starling, which was computed for this manuscript, and Epik 7.22

As expected, we found that going from an ensemble of five models (Uni-pKa) to a single model (Starling) produced a consistent but modest increase in RMSE across all benchmark sets (Table 1). Nevertheless, Starling itself maintains equal or superior accuracy to existing commercial pKa-prediction methods. Analysis of the root-mean-squared error across the pKa scale shows that the model achieves maximum accuracy in the medicinally relevant 4–12 window, while high or low pKa values are predicted with less accuracy (Figure 3).

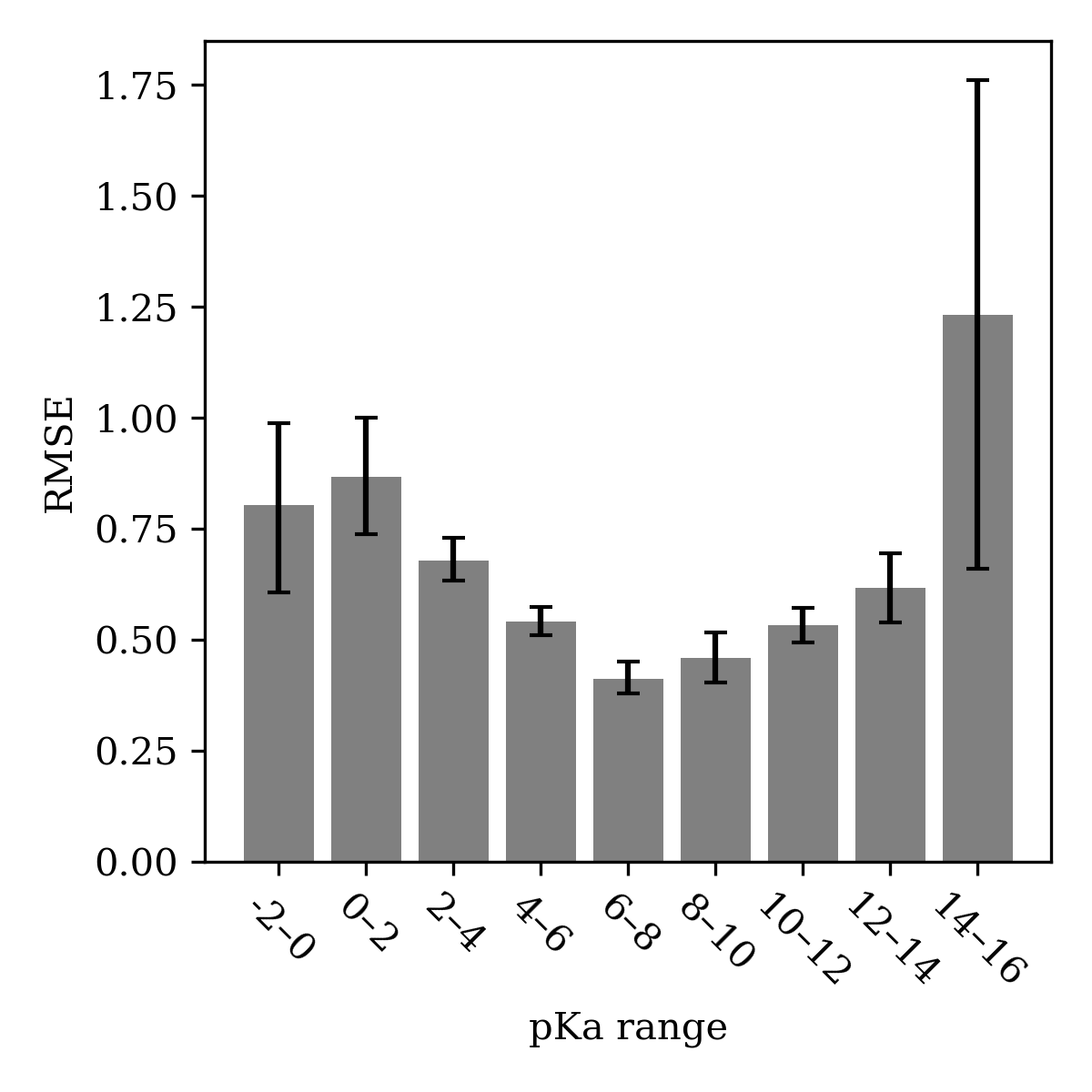
Figure 3: Root-mean-squared error across the pKa scale, as assessed on the finetuning Dwar-iBond set. Error bars denote bootstrap 95% confidence intervals (5000 samples).

At the outset of this project, we envisioned that pruning could lead to further reductions in size while maintaining useful accuracy. We applied L1-unstructured pruning to Starling to yield a further 67% reduction in size. While pruning caused minimal changes in RMSE for some benchmark sets, other benchmark sets saw substantially increased error. The pruned model also showed significant systematic error: low pKa values were overpredicted, while high pKa values were underpredicted. This led to poor performance in downstream tasks like isoelectric-point prediction (vide infra)—accordingly, we did not investigate pruning-based strategies further.

Challenging Molecules

Unlike many of the models discussed above, the Uni-pKa architecture used in Starling explicitly considers microstates, allowing it to produce reasonable predictions in more complex cases. Glycine is a particularly troublesome case, as highlighted by Zheng and co-workers—the microscopic pKa values predicted from the canonical "neutral" microstate are quite different from the macroscopic pKa values, leading to pathological behavior in many pKa prediction workflows.3 Starling correctly predicts that the zwitterionic microstate dominates at physiological pH (Figure 4), and the predicted pKa values (2.23 and 9.81) comport with experimental pKa values (2.34 and 9.60).27

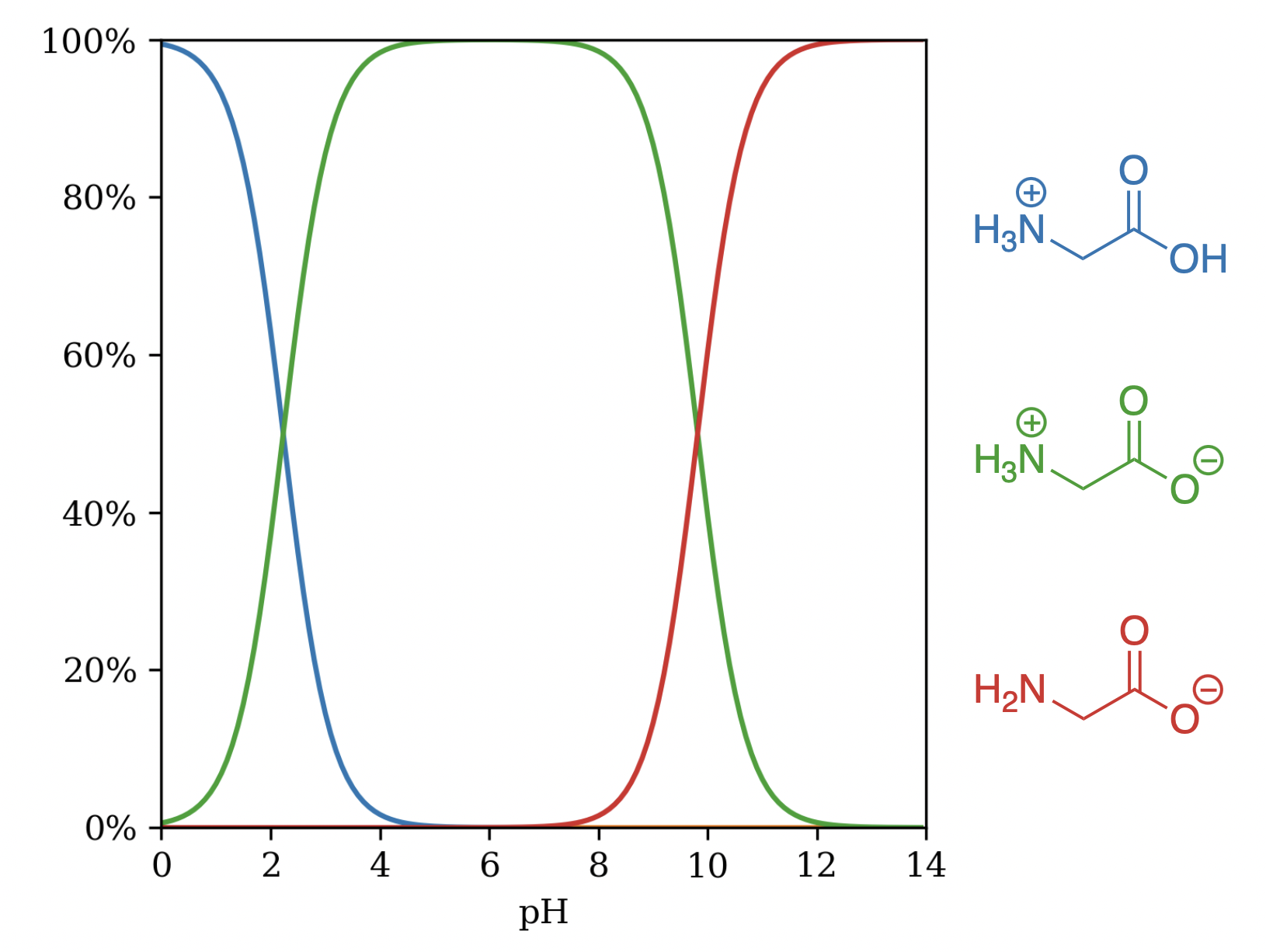
Figure 4: Significant microstates of glycine by pH.

Starling can also account for symmetry breaking in molecules containing multiple ionizable sites. Succinic acid is a C\textsubscript2-symmetric dicarboxylic acid which has experimental pKa values of 4.21 and 5.64.27 While MolGpka predicts identical pKa values of 3.4 and 3.4 for both acids,20 Starling correctly predicts non-symmetric pKa values of 3.80 and 5.10 (Figure 5). This case study highlights the advantages of considering multiple microstates, as methods that look only at the neutral microstate are fundamentally constrained to predict two identical pKa values.

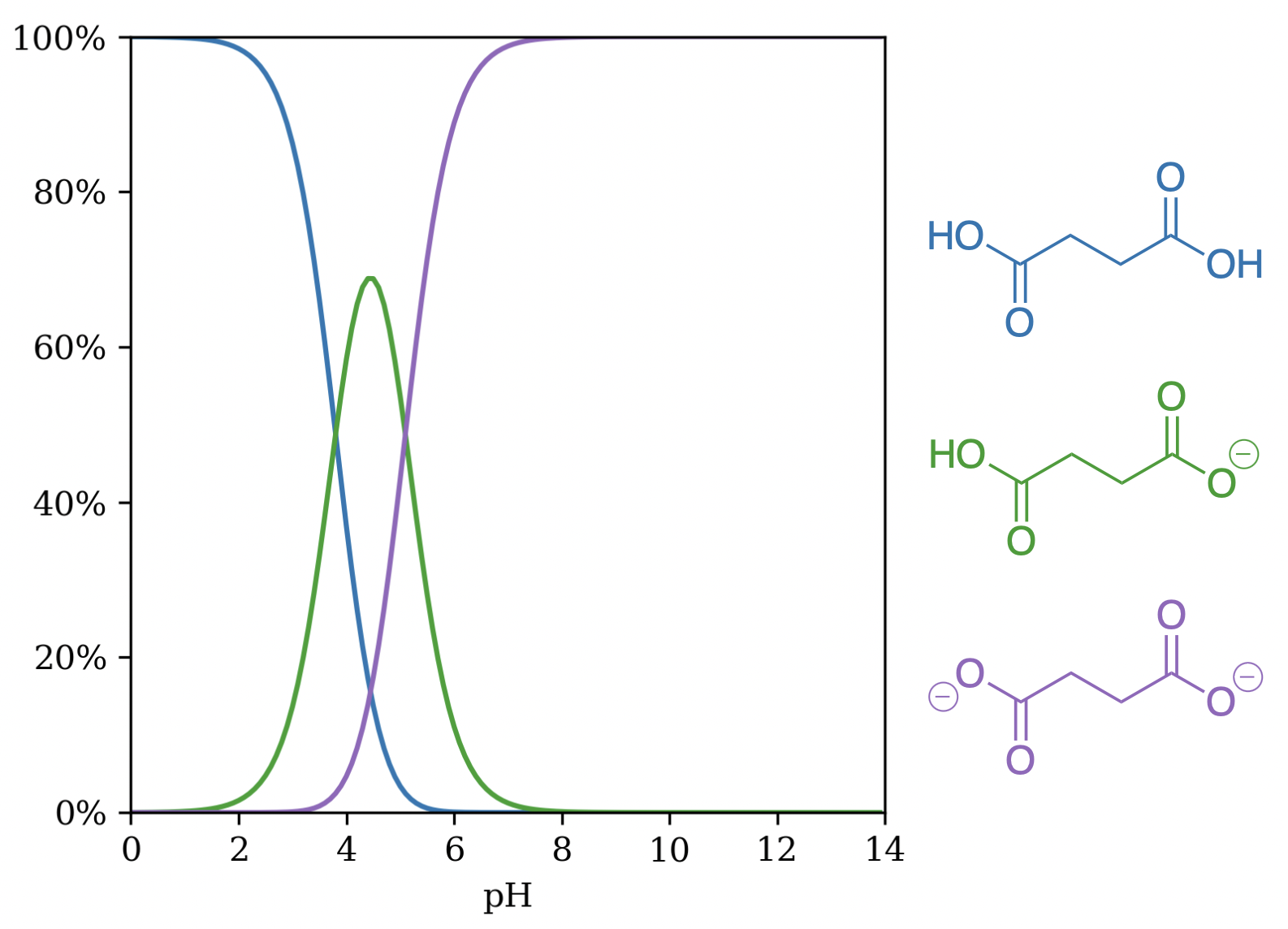
Figure 5: Unique microstates of succinic acid by pH. (Note that this approach does not differentiate between the two symmetry-equivalent singly deprotonated microstates.)

In proteolysis-targeting chimeras (PROTACs) and other bifunctional degraders, saturated N-heterocycles like piperazines are frequently found to be effective linkers.28 While the protonation state of these heterocycles has a massive impact on the physicochemical properties of the resultant molecule, predicting the effect of chemical modifications on these linkers remains challenging, and most microstate-based methods struggle with the aforementioned symmetry considerations. We evaluated Starling on a database of PROTAC-relevant fragments with associated experimental pKa values that was reported in 2022 by Jenny Desantis and co-workers.29 Starling predicts pKa values of 5.64 and 9.46 for piperazine (Figure 6), closely matching the experimental pKa values of 5.44 and 9.67. Over the entire set, Starling shows excellent performance (MAE: 0.432, RMSE: 0.668), with the biggest errors originating from the overestimation of low pKa values (Figure 7).

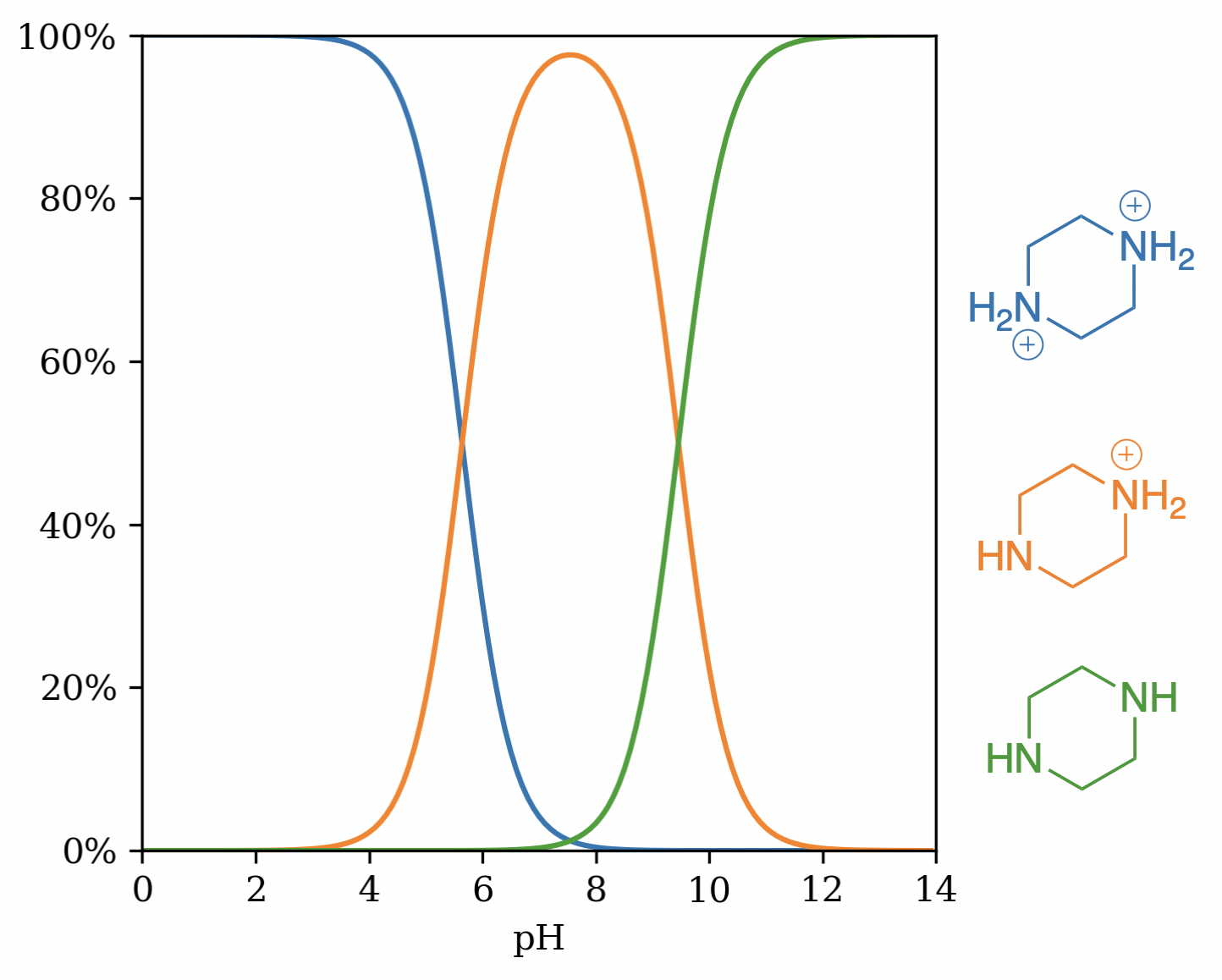
Figure 6: Unique microstates of piperazine by pH. (Note that this approach does not differentiate between the two symmetry-equivalent monoprotonated microstates.)

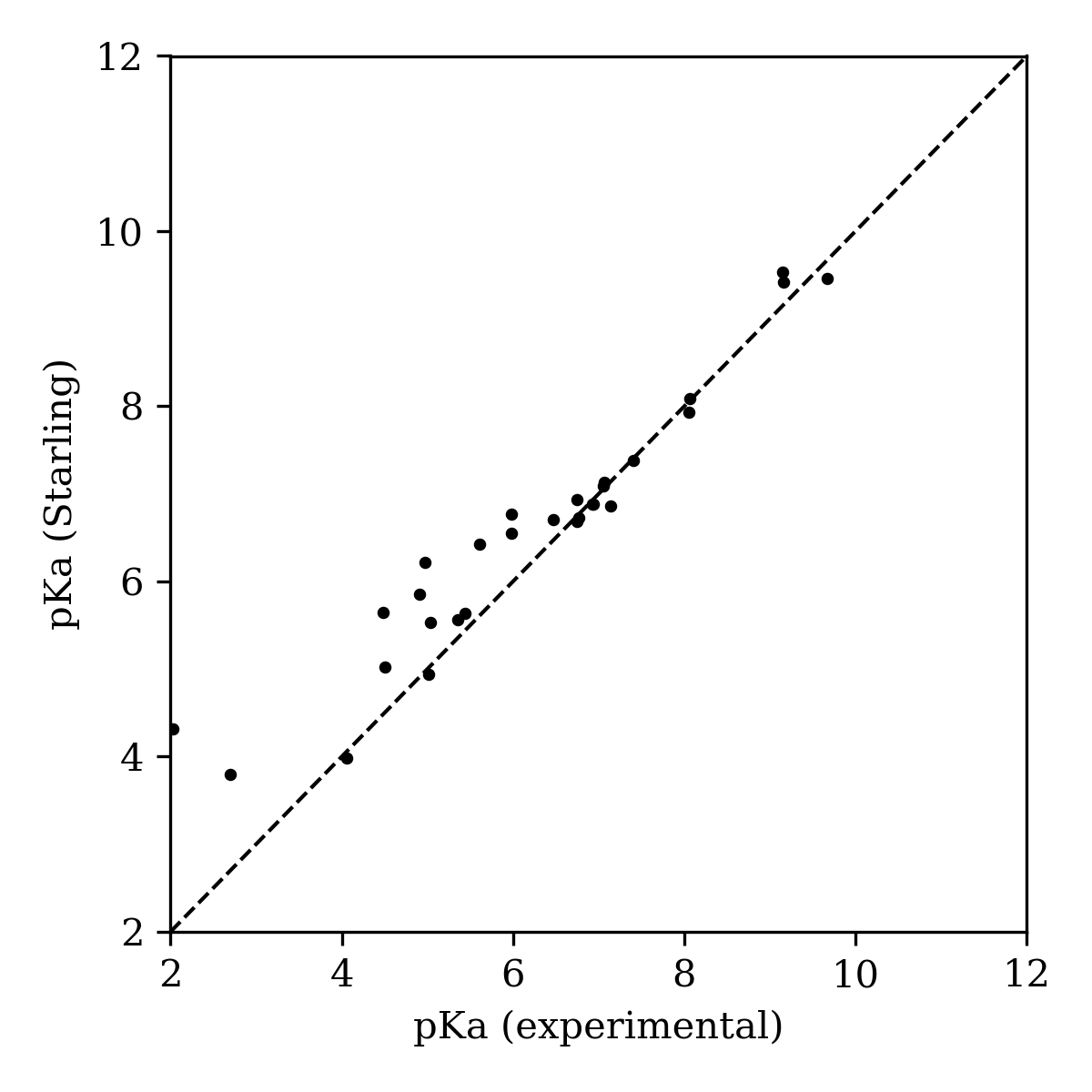
Figure 7: Performance on the Desantis PROTAC pKa dataset.29

Some limitations of the Uni-pKa architecture merit mention. While the strategy of predicting per-microstate free energies does, in general, seem more robust than direct prediction of pKa values, in certain complex cases with many similar ionizable groups the predictions can become confused and incoherent. For instance, ethylenediaminetetraacetic acid (EDTA) has six experimental pKa values and 21 relevant microstates; in this complex case, the computational predictions generated by Starling are improperly ordered and not particularly accurate (Table 2). While cases like this are currently rare in small-molecule drug discovery, we anticipate that the rise of oligopeptide therapeutics and other beyond-rule-of-five compounds will make accuracy in this regime more important moving forward, and plan to address this shortcoming in future pKa-prediction work.

Initial ChargeFinal ChargepKa (Exp.)pKa (Starling)
+2+10.002.29
+101.503.55
0-12.004.87
-1-22.693.57
-2-36.135.58
-3-410.378.37

Table 2: Comparison of experimental30 and Starling-computed pKa values for EDTA.

Microstate Distribution

As a part of the SAMPL6 pKa challenge, Ikenna Ndukwe and co-workers at Merck measured which microstates were responsible for the observed (de)protonation events for two compounds, SM07 and SM14.4 We used this experimental data to assess the accuracy of the microstates predicted by Starling. For SM07, we found that the observed protonation event at pH 6.08 was predicted to occur at pH 5.13 by Starling. NMR spectroscopy predicted that this mainly corresponded to protonation at N1 of the 4-aminoquinazoline ring, while Starling predicted that N1 protonation and aniline protonation were equally favorable (Figure 8). For SM14, Starling predicted benzimidazole protonation at pH 5.71 and aniline protonation at pH 2.48, matching the experimental microstates (pKa of 5.30 and 2.58, respectively) (Figure 8).

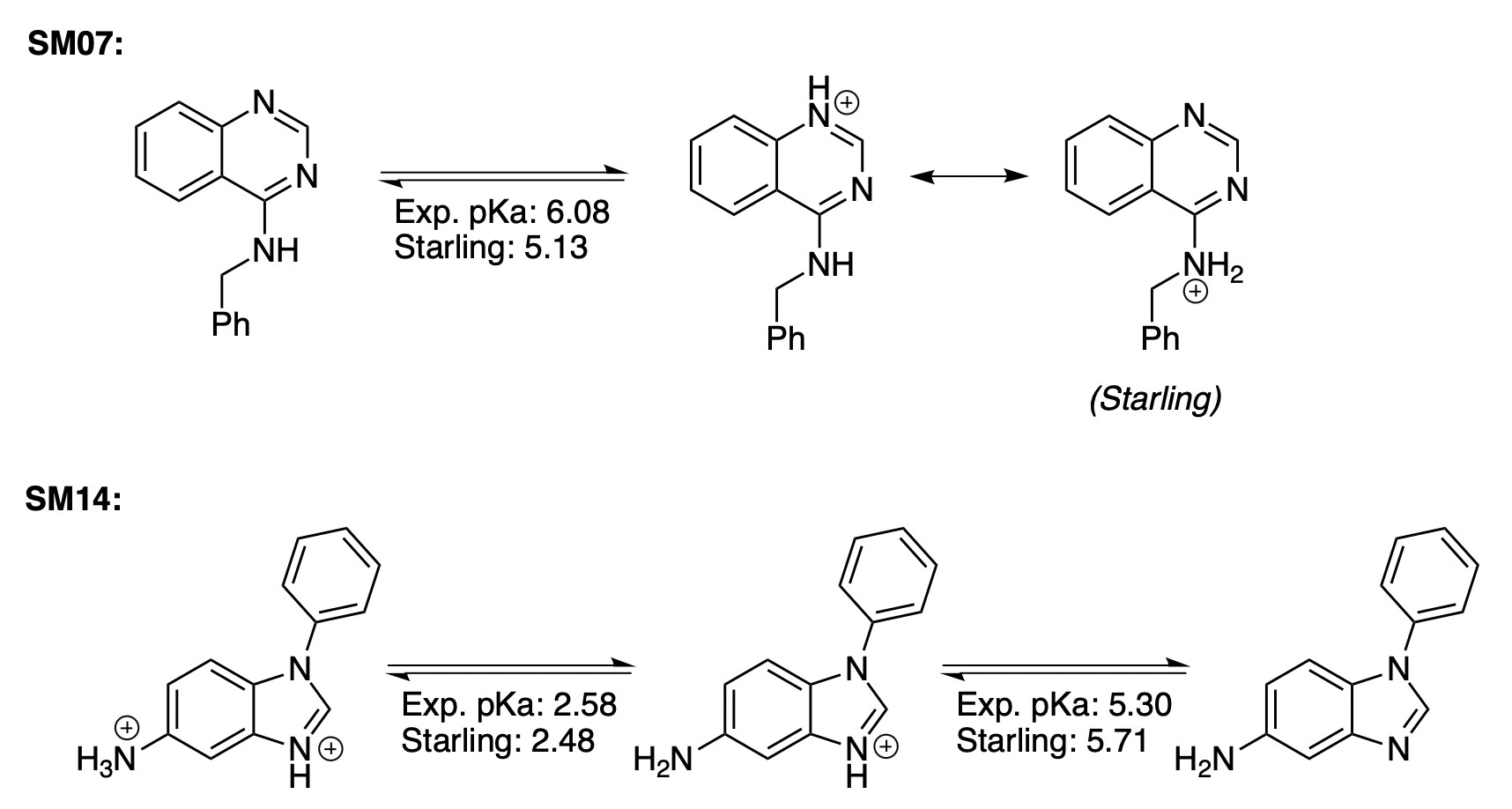
Figure 8: ChemDraw visualization of microstate transitions in SM07 and SM14.

SAMPL6 does not quantify the relative abundance of minor microstates, making it difficult to assess the accuracy of the entire microstate ensemble, but these results indicate at a minimum that training a Uni-pKa model on macroscopic pKa values yields generally reasonable microstate predictions. We note that the original Uni-pKa paper reports low accuracy on tautomer-specific benchmarks, commenting that "the model tends to attach similar free energies to different tautomers and fails to distinguish the tautomers with drastic energy differences."5 These results comport with our observations.

Isoelectric Points

With a list of pH-dependent microstate populations, determining the isoelectric point—the pH at which the average charge across all microstates is zero—is straightforward. We benchmarked the accuracy of Starling's isoelectric-point predictions for the 20 canonical amino acids, for which experimental isoelectric-point measurements are readily available.27 The Starling-predicted isoelectric points were somewhat compressed relative to experiment—high isoelectric points were underpredicted, while low isoelectric points were overpredicted (Figure 9).

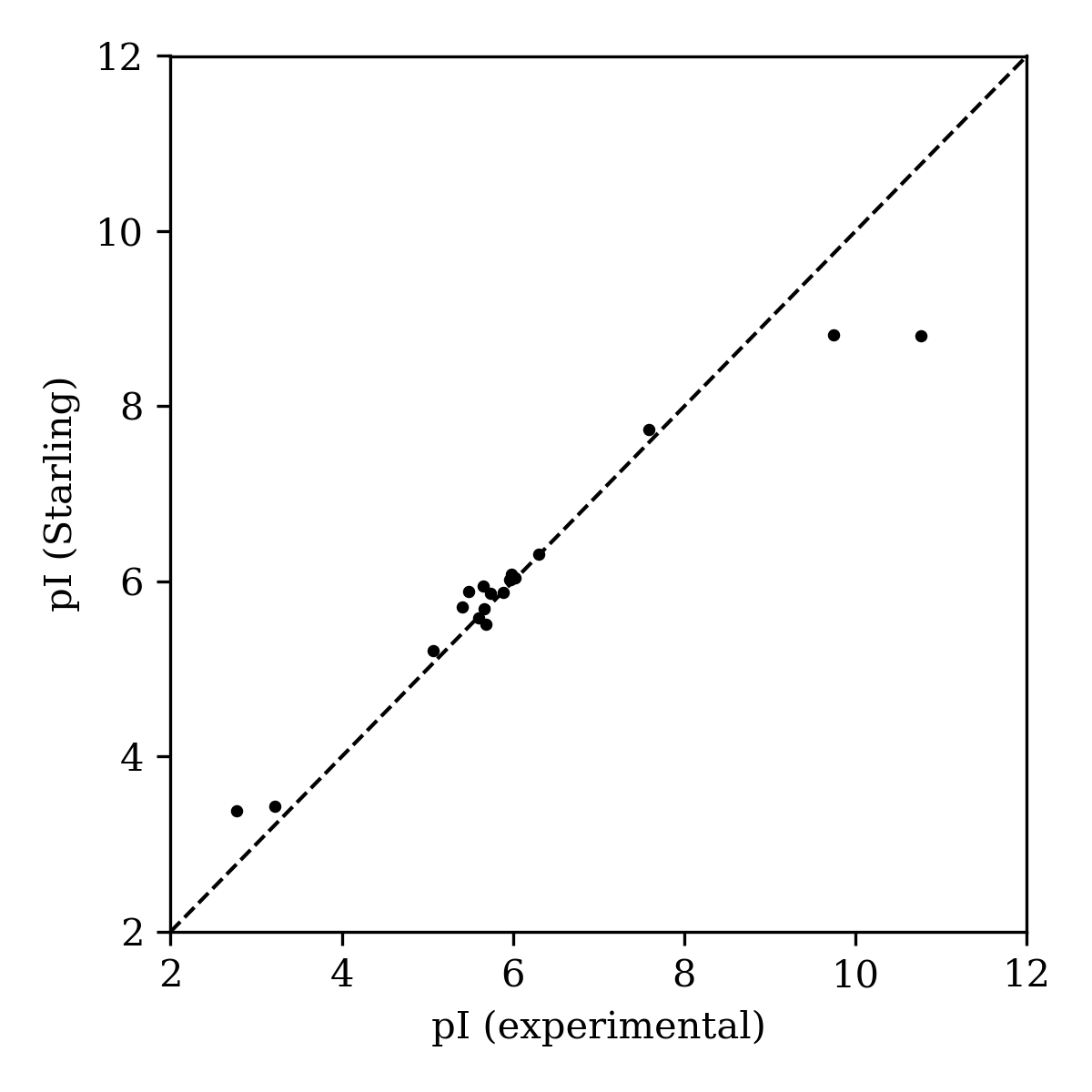
Figure 9: Experimental isoelectric points of canonical amino acids compared to Starling-predicted values.

This approach leads to good error metrics (MAE: 0.282, RMSE: 0.527) and an excellent Pearson correlation coefficient (0.979). While Starling likely underperforms modality-specific isoelectric-point-prediction algorithms like pIChemiSt,31 this approach is quick and requires no isoelectric-point-specific fine-tuning, making it a useful way to estimate the isoelectric points of novel chemical scaffolds.

logD/pH Profile Prediction

As described in the "Methods" section, the pH-dependent microstate populations produced by the global pKa prediction workflow can be used to predict logD, the distribution coefficient between water and n-octanol at a given pH. This approach gives good quantitative agreement with reported logD/pH studies for pentachlorophenol (Figure 10) and metoprolol (Figure 11).14,32 Pentachlorophenol is predicted to be highly lipophilic at low pH values, but to become hydrophilic after deprotonation at higher pH values. In contrast, the amine of metoprolol is protonated at low pH values, making the molecule strongly hydrophilic; only at higher pH is the molecule predicted to populate the octanol phase.

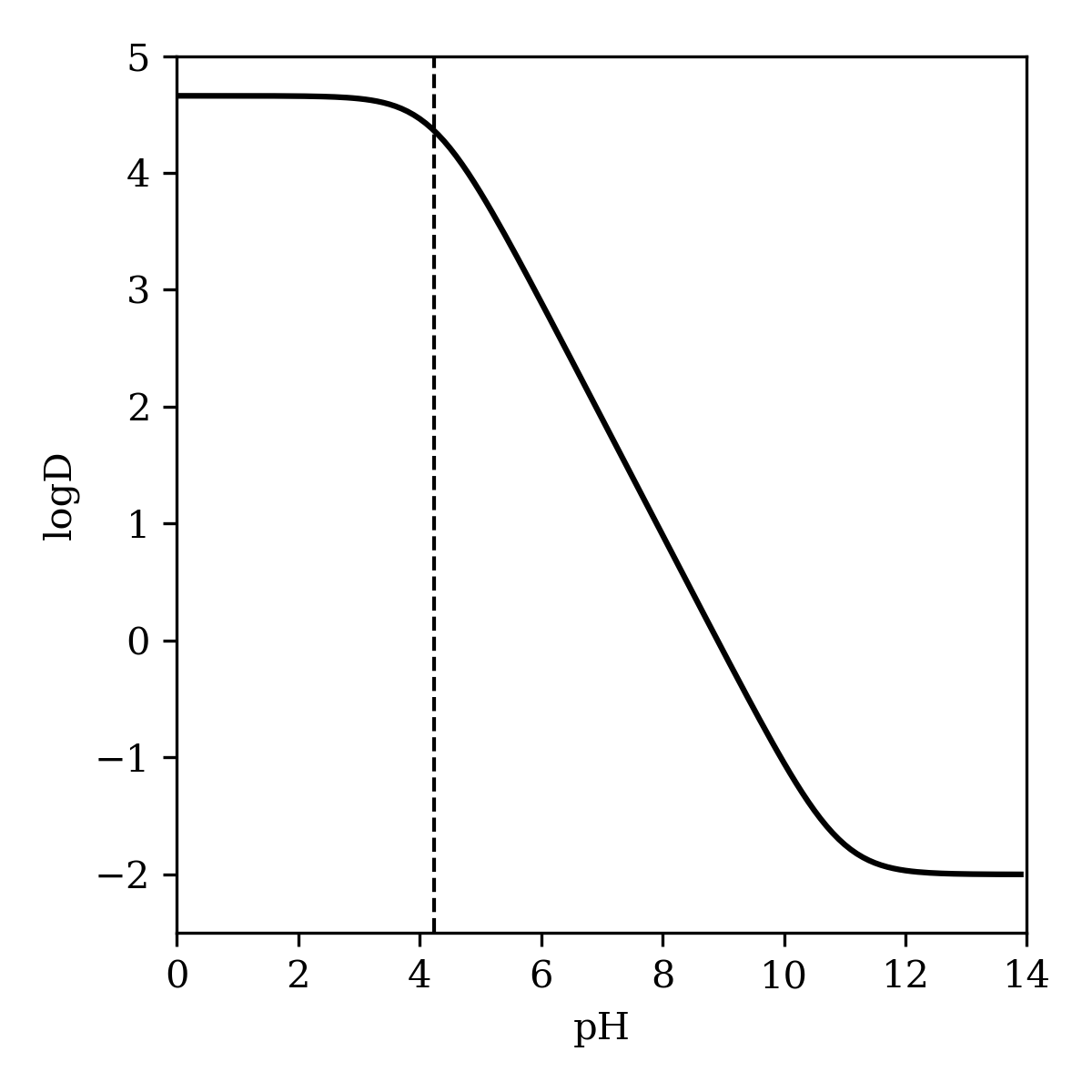
Figure 10: Predicted logD of pentachlorophenol as a function of pH. The dashed line corresponds to the predicted pKa of 4.24.

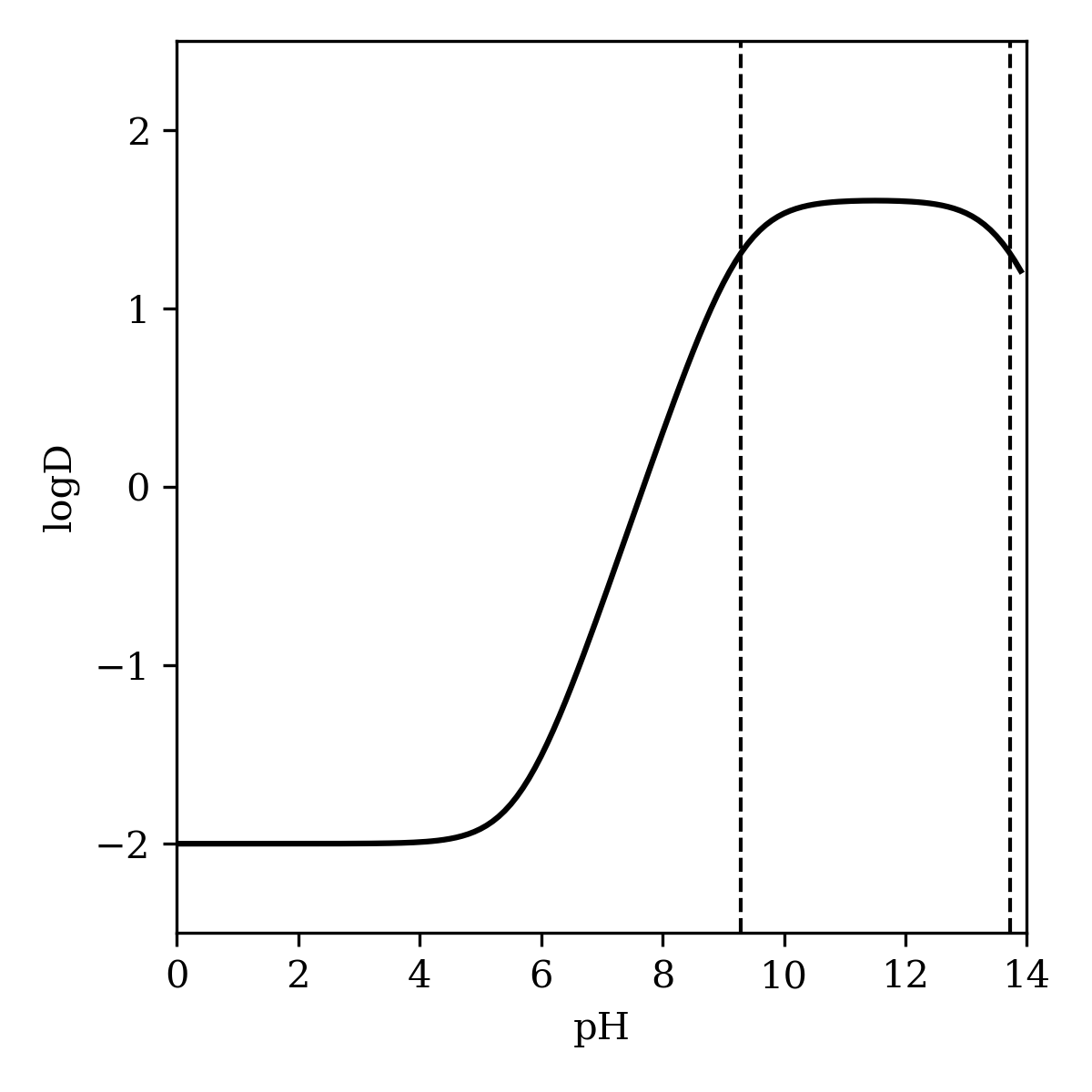
Figure 11: Predicted logD of metoprolol as a function of pH. The dashed line corresponds to the predicted pKa values of 9.29 and 13.72.

These logD predictions rely on the venerable Crippen logP-prediction scheme and, while qualitatively reasonable, are unlikely to be quantitatively accurate.13 Nevertheless, this scheme is minimally parameterized and does not require fitting to any experimental logD data, making it well-suited to extrapolation to data-scarce regions of chemical space. We expect that improvements to the underlying logP-prediction method will dramatically increase the accuracy of these predictions.

More abstractly, our approach partitions the task of predicting logD into two smaller subtasks: (1) predicting per-microstate weights at a given pH and (2) predicting logP values for a given microstate. Each of these subtasks can be independently trained and benchmarked to experimental data, making it possible to interpret errors and systematically improve the quality of output predictions. The notorious difficulty of predicting logD may stem from the fact that most logD-prediction algorithms attempt to implicitly learn both subtasks from the same dataset; we suspect that this two-task strategy may prove more tractable.

Kp,uu Prediction

Blood–brain-barrier permeability is a critical factor in developing effective central nervous system (CNS) therapeutics. The most common metric used to quantify blood–brain-barrier penetrance is unbound brain-to-plasma drug partition coefficient, or Kp,uu; in a 2022 study, over 3/4ths of drug-discovery companies surveyed found that the use of Kp,uu had a "game-changing" impact on their preclinical research.33 Unfortunately, experimental measurement of Kp,uu requires time-consuming animal studies and non-trivial amounts of material. A high-throughput computational method capable of accurate Kp,uu prediction could drive improved decision making in preclinical CNS campaigns.

Recently, Morgan Lawrenz and co-workers at Schrödinger found that the energy of solvation predicted by density-functional theory (DFT) was highly predictive of Kp,uu, the unbound brain-to-plasma ratio.16 Lawrenz and co-workers compute the solvation energy only for neutral species: to correct for cases in which the molecule is protonated at physiological pH and must undergo an uphill deprotonation, Lawrenz and co-workers add a pKa-dependent "state penalty" corresponding to the energy needed to neutralize a molecule at pH 7.4. Unfortunately, their expression only accounts for cases in which a single site on the molecule is protonated at low pH and deprotonated at high pH, making it poorly suited for complex zwitterionic cases and limiting the method's applicability to high-throughput screening or black-box usage.

We envisioned that our rapid macroscopic pKa-prediction algorithm might provide a more robust and physically accurate way of estimating the free energy of neutralization. Here, we use Starling-computed microstate weights at pH 7.4 to directly compute the free-energy penalty associated with the molecule not being in a chemically neutral, non-zwitterionic form. We also dramatically accelerate the underlying solvation energy prediction by using the AIMNet2 neural network potential to optimize conformer ensembles and computing the solvation energy using the CPCM-X implicit water model.17,18 Overall, our method is approximately two orders of magnitude faster than the reported speed of the Lawrenz workflow, and will almost certainly be faster if hardware acceleration is employed.

We evaluated our solvation-energy-prediction workflow against a dataset of 123 experimental Kp,uu values and DFT-computed solvation energies reported by Schrödinger. The solvation energies predicted by our AIMNet2/CPCM-X(water)/Starling workflow were in good agreement with the solvation energies computed at the M06-2X/LACVP**/PBF(water) // B3LYP/LACVP* level of theory. (We also note that our method does not employ any experimentally measured data, unlike the method of Lawrenz and co-workers.)

To compare the ability of both solvation-energy schemes to predict experimental Kp,uu data, log-transformed Kp,uu values were binarized at 0.3 to define a ``brain-penetrant" class (following Lawrenz and co-workers) and logistic-regression models were trained using both energy values. The model based on the Lawrenz solvation-energy workflow achieved an AUC=0.91 and 85% accuracy at a 0.5 decision threshold, while the Starling-based model yielded AUC=0.85 and 75% accuracy (mainly due to an increased number of false positives). Thus, while the high-level DFT solvation energies do yield improved categorization accuracy, AIMNet2/CPCM-X(water)/Starling-computed solvation energies remain highly predictive of experimental Kp,uu.

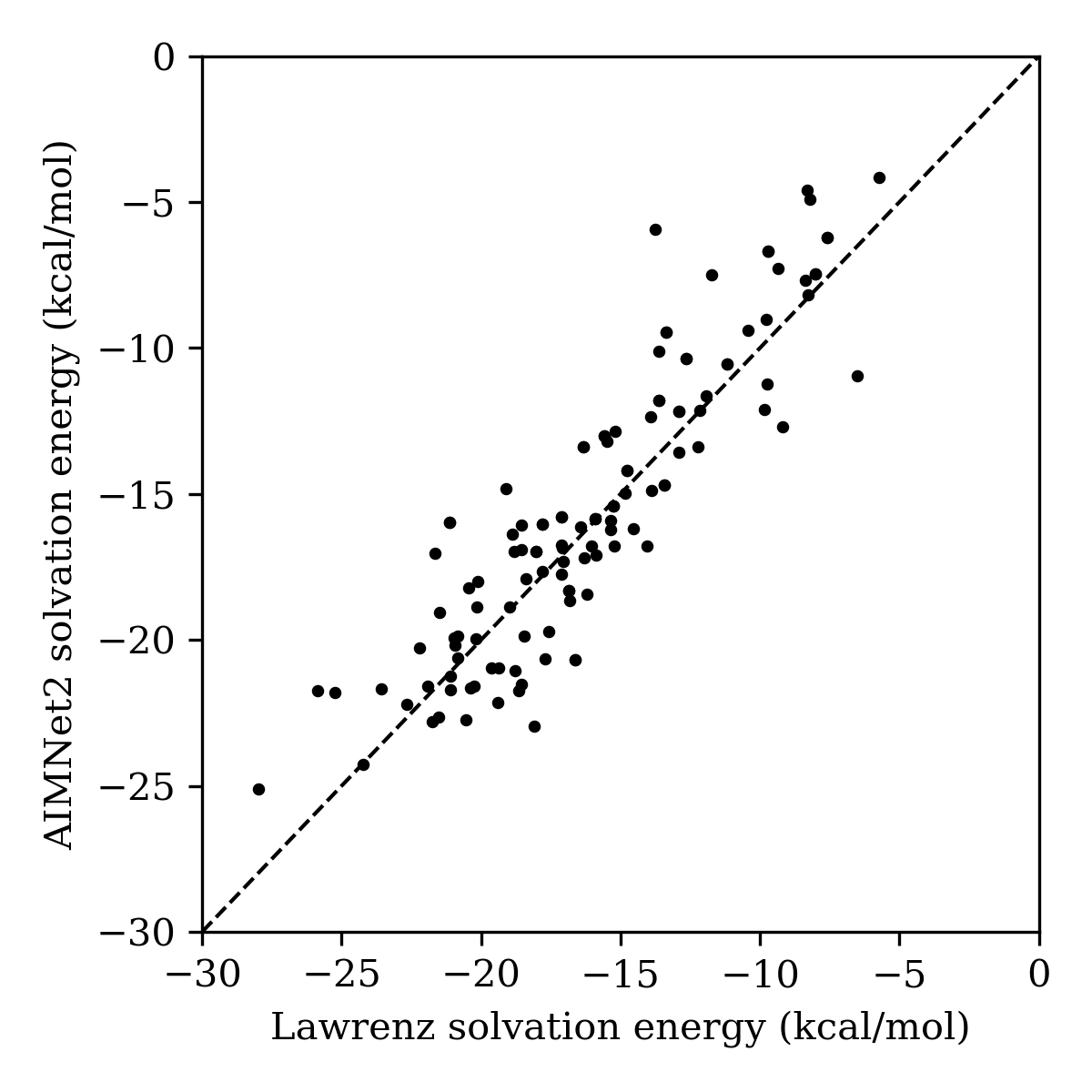
Figure 12: Comparison of DFT-based solvation energies from Lawrenz and coworkers and AIMNet2/CPCM-X(water)/Starling-computed solvation energies.

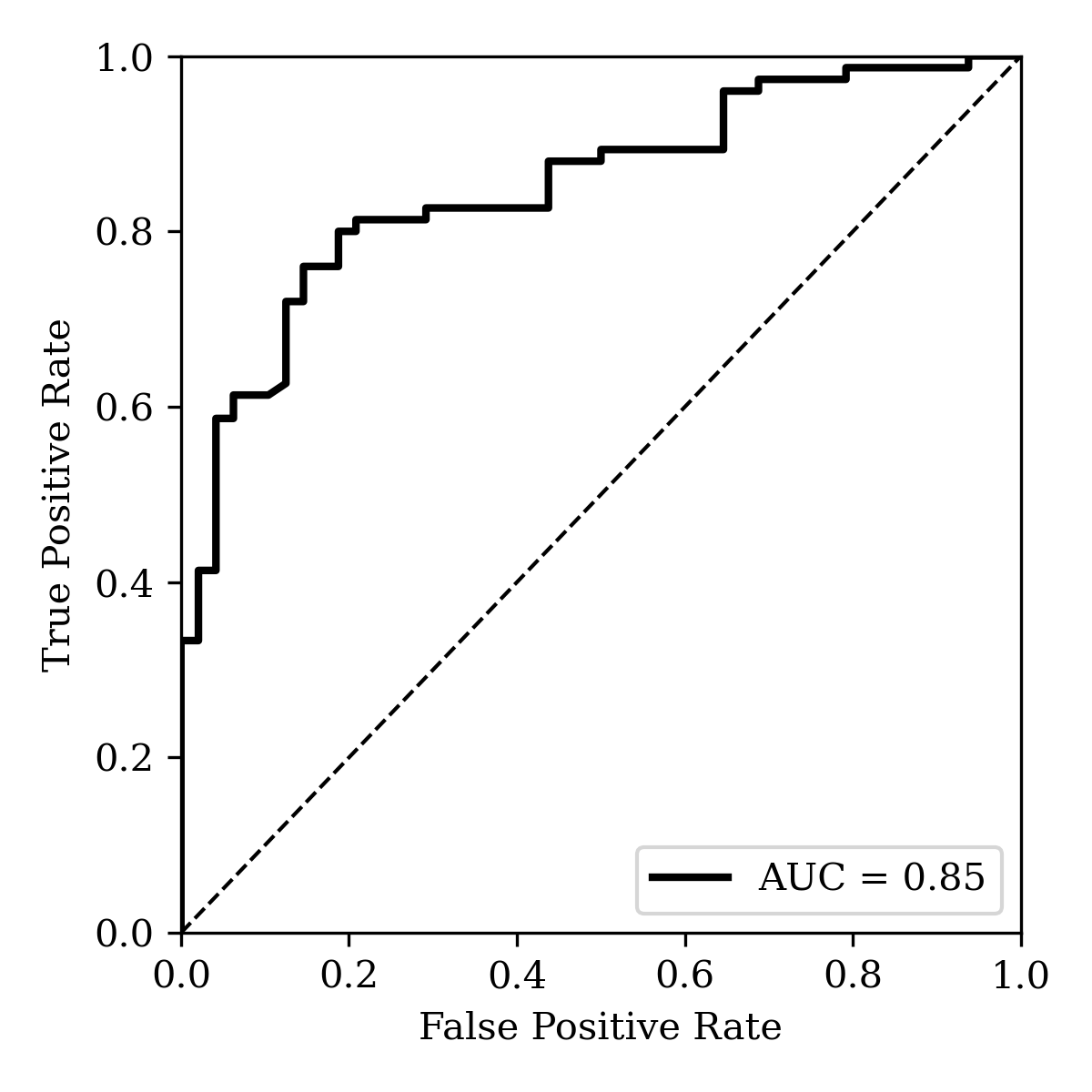
Figure 13: ROC/AUC analysis of employing AIMNet2/CPCM-X(water)/Starling-predicted energy of solvation to predict Kp,uu at a threshold of 0.3.

Conclusion

We present Starling, a lightweight, physics-informed neural network for macroscopic pKa prediction. Starling explicitly resolves microstate ensembles and their populations, enabling the prediction of derived properties including logD, isoelectric point, and neutralization free energy—all from a single forward pass. Furthermore, the underlying free-energy-prediction scheme employed by the Uni-pKa architecture make Starling robust to failure modes common to other pKa-prediction methods. We expect Starling to be capable of generating immediate practical insights in medicinal chemistry, from estimating logD/pH profiles to guiding the development of CNS-active therapeutics through rapid blood–brain-barrier predictions.

Nevertheless, considerable theoretical improvements to Starling are possible. Because the Uni-pKa architecture explicitly resolves the microstate ensemble, it can naturally accommodate new multiobjective training targets: tautomer equilibrium data, experimental isoelectric points, experimental logD measurements, and more. This flexibility could allow similar microstate-scoring architectures to incorporate larger and more diverse datasets. We anticipate that further efforts in this area can address the limitations of Starling and reach unprecedented levels of accuracy for physicochemical property-prediction tasks.

Acknowledgement

C.C.W. thanks Ari Wagen, Jonathon Vandezande, Elias Mann, and Spencer Schneider for editing drafts of this manuscript. C.C.W also thanks Jonathan Zheng for helpful discussions.

References

  1. Di, L.; Kerns, E. H. Drug-Like Properties: Concepts, Structure Design and Methods from ADME to Toxicity Optimization, 2nd ed.; Academic Press: Boston, 2016.
  2. Navo, C. D.; Jiménez-Osés, G. Computer Prediction of pKa Values in Small Molecules and Proteins. ACS Med. Chem. Lett. 2021, 12, 1624–1628.
  3. Zheng, J. W.; Leito, I.; Green, W. H. Widespread Misinterpretation of pKa Terminology for Zwitterionic Compounds and Its Consequences. J. Chem. Inf. Model. 2024, 64, 8838–8847.
  4. Işık, M.; Rustenburg, A. S.; Rizzi, A.; Gunner, M. R.; Mobley, D. L.; Chodera, J. D. Overview of the SAMPL6 pKa Challenge: Evaluating Small Molecule Microscopic and Macroscopic pKa Predictions. J. Comput.-Aided Mol. Des. 2021, 35, 131–166.
  5. Luo, W. et al. Bridging Machine Learning and Thermodynamics for Accurate pKa Prediction. JACS Au 2024, 4, 3451–3465.
  6. Pretrained Models For Inference? GitHub issue comment, https://github.com/dptech-corp/Uni-pKa/issues/3#issuecomment-2604100717 (accessed 2025-04-18).
  7. Hsu, F. Common Starling at Half Moon Bay. https://en.wikipedia.org/wiki/Common_starling, 2018.
  8. RDKit: Open-source cheminformatics. https://www.rdkit.org. https://www.rdkit.org, 2013–2025.
  9. Plata, R. E.; Singleton, D. A. A Case Study of the Mechanism of Alcohol-Mediated Morita Baylis–Hillman Reactions. The Importance of Experimental Observations. J. Am. Chem. Soc. 2015, 137, 3811–3826.
  10. Riniker, S.; Landrum, G. A. Better Informed Distance Geometry: Using What We Know To Improve Conformation Generation. J. Chem. Inf. Model. 2015, 55, 2562–2574.
  11. Wang, S. et al. Improving Conformer Generation for Small Rings and Macrocycles Based on Distance Geometry and Experimental Torsional-Angle Preferences. J. Chem. Inf. Model. 2020, 60, 2044–2058.
  12. Halgren, T. A. Merck molecular force field. I. Basis, form, scope, parameterization, and performance of MMFF94. J. Comput. Chem. 1996, 17, 490–519.
  13. Wildman, S. A.; Crippen, G. M. Prediction of Physicochemical Parameters by Atomic Contributions. J. Chem. Inf. Comput. Sci. 1999, 39, 868–873.
  14. Chen, C.-S.; Lin, S.-T. Prediction of pH Effect on the Octanol–Water Partition Coefficient of Ionizable Pharmaceuticals. Ind. Eng. Chem. Res. 2016, 55, 9284–9294.
  15. Avdeef, A. pH-Metric log P. II: Refinement of partition coefficients and lonization constants of multiprotic substances J. Pharm. Sci. 1993, 82, 183–190.
  16. Lawrenz, M. et al. A Computational Physics-based Approach to Predict Unbound Brain-to-Plasma Partition Coefficient, Kp,uu. J. Chem. Inf. Model. 2023, 63, 3786–3798.
  17. Anstine, D.; Zubatyuk, R.; Isayev, O. AIMNet2: A Neural Network Potential to Meet Your Neutral, Charged, Organic, and Elemental-Organic Needs. ChemRxiv, 2024.
  18. Stahn, M.; Ehlert, S.; Grimme, S. Extended Conductor-like Polarizable Continuum Solvation Model (CPCM-X) for Semiempirical Methods. J. Phys. Chem. A 2023, 127, 7036–7043.
  19. Wang, L.-P.; Song, C. Geometry optimization made simple with translation and rotation coordinates. J. Chem. Phys. 2016, 144, 214108.
  20. Pan, X. et al. MolGpka: A Web Server for Small Molecule pKa Prediction Using a Graph-Convolutional Neural Network. J. Chem. Inf. Model. 2021, 61, 3159–3165.
  21. Shelley, J. C. et al. Epik: a software program for pK( a ) prediction and protonation state generation for drug-like molecules. J. Comput.-Aided Mol. Des. 2007, 21, 681–691.
  22. Johnston, R. C. et al. Epik: pKa and Protonation State Prediction through Machine Learning. J. Chem. Theory Comput. 2023, 19, 2380–2388.
  23. Abarbanel, O. D.; Hutchison, G. R. QupKake: Integrating Machine Learning and Quantum Chemistry for Micro-pKa Predictions. J. Chem. Theory Comput. 2024, 20, 6946–6956.
  24. Machine learning meets pKa. https://github.com/czodrowskilab/Machine-learning-meets-pKa (accessed 2025-04-18).
  25. Grosjean, H. et al. SAMPL7 Protein-Ligand Challenge: A community-wide evaluation of computational methods against fragment screening and pose-prediction. J. Comput.-Aided Mol. Des. 2022, 36, 291–311.
  26. The SAMPL8 Blind Prediction Challenges for Computational Chemistry. https://github.com/samplchallenges/SAMPL8 (accessed 2025-04-18).
  27. Gokel, G. W.; Dean, J. A. Dean's handbook of organic chemistry, 2nd ed.; McGraw-Hill: New York, 2004.
  28. Troup, R. I.; Fallan, C.; Baud, M. G. J. Current strategies for the design of PROTAC linkers: a critical review. Explor. Target. Anti-tumor Ther. 2020, 1, 273–312.
  29. Desantis, J. et al. PROTACs bearing piperazine-containing linkers: what effect on their protonation state? RSC Adv. 2022, 12, 21968–21977.
  30. Harris, D. C. Quantitative Chemical Analysis, 8th ed.; Macmillan Learning: New York, 2010.
  31. Frolov, A. I. et al. pIChemiSt Free Tool for the Calculation of Isoelectric Points of Modified Peptides. J. Chem. Inf. Model. 2023, 63, 187–196.
  32. Markovic, M. et al. Segmental-Dependent Solubility and Permeability as Key Factors Guiding Controlled Release Drug Product Development. Pharmaceutics 2020, 12.
  33. Loryan, I. et al. Unbound Brain-to-Plasma Partition Coefficient, Kp,uu,brain—A Game Changing Parameter for CNS Drug Discovery and Development. Pharm. Res. 2022, 39, 1321–1341.
Banner background image

What to Read Next

Starling: Macroscopic pKa, logD, and Blood–Brain-Barrier Permeability

Starling: Macroscopic pKa, logD, and Blood–Brain-Barrier Permeability

microscopic vs. macroscopic pKa; Uni-pKa and Starling; microstate ensembles; logD and Kp,uu predictions
Apr 25, 2025 · Corin Wagen
Physics-Informed Machine Learning Enables Rapid Macroscopic pKa Prediction

Physics-Informed Machine Learning Enables Rapid Macroscopic pKa Prediction

Here we introduce Starling, a physics-informed neural network based on the Uni-pKa architecture trained to predict per-microstate free energies and compute macroscopic pKa values via thermodynamic ensemble modeling.
Apr 25, 2025 · Corin C. Wagen
Predicting Infrared Spectra and Orb-v3

Predicting Infrared Spectra and Orb-v3

light and its manifold interactions with matter; why IR spectroscopy is useful; predicting IR spectra through Rowan; Orb-v3
Apr 17, 2025 · Ari Wagen, Corin Wagen, and Jonathon Vandezande
What's in a Name?

What's in a Name?

Why our company is named after a tree with no obvious connection to what we do.
Apr 11, 2025 · Corin Wagen and Ari Wagen
2D Scans, More Fukui Options, & Max Concurrency

2D Scans, More Fukui Options, & Max Concurrency

escape from scan-land; making More O'Ferrall–Jencks plots in Rowan; extending Fukui calculations to more levels of theory; managing large numbers of concurrent jobs
Apr 10, 2025 · Corin Wagen, Ari Wagen, Spencer Schneider, and Jonathon Vandezande
Can AI Can Accelerate Scientific Research?

Can AI Can Accelerate Scientific Research?

New research from Aiden Toner-Rodgers at MIT suggests the answer is yes, but with important caveats.
Apr 2, 2025 · Corin Wagen
"Glitch Mode" and Concerted Scans

"Glitch Mode" and Concerted Scans

the longue durée history of human communication; today only, a new modality in scientific visualization; concerted scans
Apr 1, 2025 · Corin Wagen and Ari Wagen
Rowan Research Spotlight: Ameer Nizami

Rowan Research Spotlight: Ameer Nizami

How Rowan helps Concordia researchers discover better batteries.
Mar 25, 2025 · Corin Wagen
Modeling Addition and Substitution Reactions

Modeling Addition and Substitution Reactions

Modeling addition and substition reaction thermodynamics for cyclohexane and benzene with diatomic bromine.
Mar 20, 2025 · Milca Pierre and Ari Wagen
Protein–Ligand Docking

Protein–Ligand Docking

critical contemplation of the merits and demerits of docking; unphysical poses and how to find them; machine learning offers a pragmatic solution; running docking on Rowan; future protein aspirations
Mar 14, 2025 · Ari Wagen, Corin Wagen, and Spencer Schneider