The "Charlotte's Web" of Density-Functional Theory (DFT)
by Jonathon Vandezande · Dec 20, 2024 · updated Oct 27, 2025
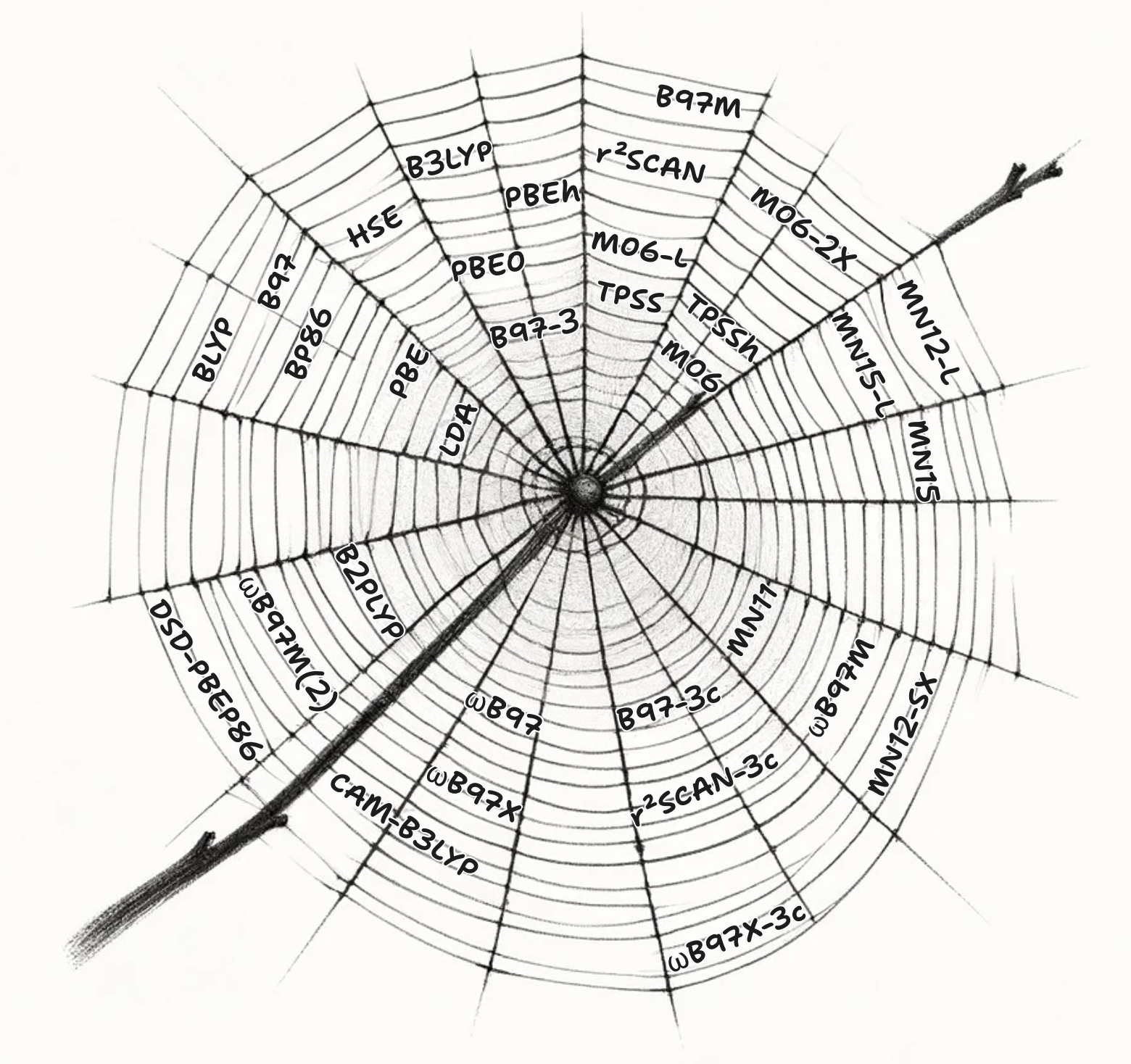
The "Charlotte's web" of density functionals (jump to the web)
Density-functional theory (DFT) is a cornerstone of modern computational quantum chemistry, offering a balance between computational efficiency and accuracy. Unlike Hartree–Fock (HF) and wavefunction-based methods, which explicitly solve for the electronic wavefunction, DFT focuses on the electron density, , to predict the properties and energies of molecular and condensed matter systems. This essay explains the foundational principles of DFT, the evolution of exchange–correlation functionals, and the myriad corrections developed to address DFT's limitations.
This guide contains the following sections:
- Theoretical Background
- Key Concepts in DFT
- Local (Spin) Density Approximation (LDA/LSDA)
- Density Inhomogeneity
- Inclusion of Hartree–Fock Exchange
- Correlation
- Machine-Learned Functionals
- Charlotte's Web
- External Corrections
- Conclusion
Theoretical Background
(We advise most readers to skim through or skip this section.)
DFT is grounded in two theorems from Hohenberg and Kohn (1964):
- The ground-state energy of an interacting electron system is uniquely determined by the electron density .
- The functional that provides the ground-state energy achieves its minimum value for the true ground-state density.
Kohn and Sham extended this framework by introducing non-interacting electrons that reproduce the same density as the interacting system. The total energy functional in Kohn–Sham DFT is expressed as:
where:
- is the kinetic energy of non-interacting electrons,
- is the external potential energy,
- is the classical Coulomb energy, and
- is the exchange–correlation energy, incorporating all quantum many-body effects.
The success of DFT hinges on , which must be approximated since its exact form is unknown.
Key Concepts in DFT
"Electron exchange" is the quantum mechanical effect enforcing the Pauli exclusion principle. This term describes the reduction in Coulomb repulsion between electrons due to the antisymmetry of the wavefunction, effectively lowering the total energy.
"Electron correlation" is the interaction between electrons that is not captured via the mean-field approximation (Hartree–Fock theory), but instead reflects individual electron–electron interactions.
And:
- is electron density.
- is the derivative of electron density.
- refers to molecular orbital .
Local (Spin) Density Approximation (LDA/LSDA)
Since the exact form of the "true density functional" from Hohenberg and Kohn is not known, simple models are used to approximate the physics and functionals are evaluated on a grid, to make the calculations tractable.
For an infinite homogeneous electron gas, the exchange–correlation functional would be . Early approximations such as the local-density approximation (LDA) and its open-shell analogue, the local-spin-density approximation (LSDA), evaluate each point on the grid as though it were part of this homogeneous gas (often called the uniform electron density approximation):
While far less accurate than post-HF wavefunction methods, it is very easy to calculate and was useful for early computational work. LDA models tend to underestimate the exchange contribution and overestimate the correlation. Because of this, LDA predicts binding energies which are too large and bond distances which are too short.
There have been a variety of attempts to improve the LDA model, which have been likened to climbing Jacob's ladder, but the variety of directions that have been taken make it perhaps more like Charlotte's web.
The following improvements to LDA will be discussed herein:
- Description of inhomogeneity in the density
- Inclusion of HF exchange
- Dispersion corrections
- Post-SCF corrections to correlation
Additionally, since finite basis sets are used, additional corrections have been developed that better replicate the complete basis set limit without changing the functional form:
Density Inhomogeneity
One of the simplest ways to correct the LDA exchange correlation functional is to move from a model of uniform electron density to one with inhomogeneous density by evaluating the exchange correlation part of the functional on both the density and its derivatives.
Generalized Gradient Approximation (GGA)
Including the first derivative of the density, , in the functional evaluation leads to the generalized-gradient approximation (GGA, also referred to as semi-local DFT), which calculates exchange-correlation energy as:
BLYP was the first widely successful GGA, and provided a significant improvement in molecular properties over LDA. GGAs are generally useful for geometry optimizations, but tend to perform poorly for energetics.
meta-Generalized Gradient Approximation (mGGA)
Including the kinetic energy density (or occasionally the Laplacian of the density, ) can further improve the properties, and is referred to as a meta-generalized gradient approximation (abbreviated meta-GGA or mGGA), calculating exchange–correlation energy as:
mGGAs provide significantly more accurate energetics than GGAs, at only slightly increased cost. However, they can be more sensitive to grid effects, requiring larger grid sizes and higher computational cost.
meta-Nonseparable Gradient Approximation (mNGA)
Higher order corrections have been tried, such as the meta-nonseparable gradient approximation (mNGA), but have not yet found significant use in computational workflows.
Table 1: Select pure DFT functionals
Inclusion of Hartree–Fock Exchange
"Pure" density functionals discussed above suffer from self-interaction error (SIE) due to each electron interacting with the entire electron cloud (including its own contribution to the electron cloud) and incorrect asymptotic behavior of the exchange–correlation potential. Consequently, valence orbital energies are overestimated and HOMO–LUMO gaps are systematically underestimated. This is especially detrimental for electron-rich species, as the improper asymptotic form hinders their ability to effectively bind the additional electrons.
Hybrids
Hartree–Fock (HF) exchange does not suffer from SIE or incorrect asymptotic behavior; in fact, HF tends to underbind and have bond distances which are too long (the exact opposite of "pure" density functionals). Hybrid density functionals combine DFT exchange (also termed local exchange) and HF exchange (also termed nonlocal exchange) to provide cancellation of errors and more accurate results, calculating exchange–correlation energy as:
where is a mixing parameter indicating the fraction of the exchange coming from HF (e.g., in B3LYP).
Popularized in 1993 with the B3PW91 density functional, HF exchange has conventionally been of the global variety, meaning that the fraction of HF exchange is uniform for all inter-electronic distances. The inclusion of HF exchange significantly increases the accuracy relative to non-hybrid (pure) functionals, but at a large increase in computational cost due to the need to construct the exact exchange matrix, which scales poorly with increasing system size.
Table 2: Select hybrid DFT functionals
Range-Separated Hybrids (RSH)
Since HF has the correct asymptotic behavior for the XC potential, but does poorly for short-ranged interactions, while DFT is the opposite, it can also be useful to combine them in a non-uniform manner, with a stronger HF contribution at long-range and a stronger DFT contribution at short range. Typically formulated as range-separated hybrids (RSH), the exchange functions are mixed using the error function or similar shapes to smoothly transition between the exchanges, calculating exchange–correlation energy as:
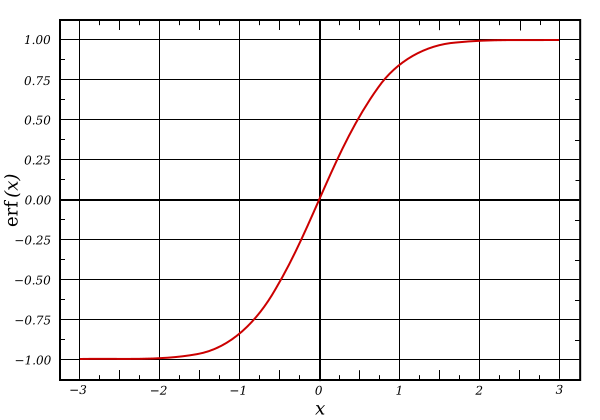
Figure 1: The error function shape (public domain)
Range-separated hybrids are useful when bonds are stretched (such as in transition states), charge is unevenly shared (e.g. charge-transfer species and zwitterions), or molecules are in excited states. They can also help prevent the collapse of the HOMO–LUMO gap due to unphysical charge delocalization from pure functionals and global hybrids.
Table 3: Select range-separated hybrid DFT functionals
Screened Hybrids
Screened functionals have the HF exchange smoothly decrease to 0, and are useful for improving the speed (due to the cost of long-range HF exchange) and SCF convergence properties for large molecules. While they do not see significant use in molecular DFT, they can provide a significant benefit in periodic DFT where global hybrids are often too expensive.
Table 4: Select screened hybrid DFT functionals
Correlation
The correlation functional in DFT underestimates long-range interactions due to its local nature, and both DFT and HF completely neglect dispersion (van der Waals forces). While these interactions are often individually small, they can provide a significant contribution to larger systems and intermolecular interactions.
Dispersion
In both DFT and HF, regions of positive and negative charge in the density do not attract each other due to being mean-field theories. This can easily be corrected with a damped, atom–atom potential (e.g. D, D2, D3, D30, D3(BJ), D4) or non-local correlation (e.g. VV10, vdW-Df-2). Typically calculated in multipole-expansion form as:
Dispersion corrections have become the standard for modern DFT calculation, as they add negligible computational cost and provide a significant increase in accuracy.
Post-SCF Corrections
Correlation can also be included in a wavefunction-like manner, with the addition of post-SCF corrections. Double hybrids utilizing MP2 and its spin-component-scaled variants provide some of the highest accuracy DFT calculations. It can even rival CCSD(T) for main-group thermochemistry, kinetics, and noncovalent interactions, but at significantly lower cost.
However, MP2 correlation still scales as O(N5) (i.e. doubling the system size increases cost by 25 = 32), making it significantly more expensive than even RSH DFT. Various improvements include using only the opposite spin (OS) component of the MP2 correlation energy (ia|jb), which scales as O(N4) or utilizing local methods such as DLPNO.
Double hybrids can be improved in an analogous manner to range-separated hybrids, with range-separated double hybrids smoothly interpolating between the correlation functional and the double-hybrid correction.
Double hybrids perform poorly for systems with small HOMO–LUMO gaps, where there is significant static correlation. Double hybrids with smaller amounts of HF exchange tend to perform better for transition metal chemistry due to their better description of static correlation, while double hybrids approaching 25–50% HF exchange tend to perform better for main-group thermochemistry and barrier heights due to the decreased self-interaction error.

Figure 2: Double-hybrid-functional recommendations from Goerigk and Grimme (2014)
| X → Hybridicity ↓ | GGA – | mGGA – |
|---|---|---|
| (Global-) Double Hybrid | B2-PLYP, DSD-PBEP86 | |
| Range-Separated Double Hybrid | B2-P3LYP, ωB97X-2 | ωB97M(2) |
Table 5: Selected double-hybrid functionals. All selected range-separated hybrids include range separation for both the exchange and MP2 correlation.
Machine-Learned Functionals
Most useful functionals have empirically fit parameters, with optimal selection of the number and values for each of these parameters being an area of active research as new functionals are developed. A logical extension of this is to use ML to learn the functional's parameters, predict the Hamiltonian values directly, or correct pure functionals with non-local exchange.
Early work by Tozer, Ingamells, and Handy showed the effectiveness of using a neural network to represent the formally exact Zhao, Morrison, Parr (ZMP) potential. The neural net learned the ZMP potential with only the density as input and a single hidden layer with 8 nodes. It managed to outperform LDA, mostly due to the improved long-range behavior (the exchange term in pure functionals decays as instead of the correct )
More recent developments include the Skala ML-functional, which takes as input 7 semi-local meta-GGA descriptors:
- density:
- gradient norm:
- kinetic energy:
It uses a multi-layer perceptron (MLP) to create a spin-symmetrized local hidden representation and projects these features to a lower-dimensional hidden vector. The coarse grid of points collects non-local interactions and reassembles them with a soft partitioning. These local and non-local features are fed into a final MLP which produces an enhancement factor for the local density. Finally, an integration is carried out over all points as in traditional DFT to arrive at the .
Figure 3: Architecture of the Skala ML-functional from Luise et al. (2025)
Charlotte's Web
| X → Hybridicity ↓ | Local | GGA – | mGGA – | mNGA |
|---|---|---|---|---|
| Pure (non-hybrid) | LDA | BLYP, BP86, B97, PBE | TPSS, M06-L, r2SCAN, B97M | MN12-L, MN15-L |
| (Global-) Hybrid | B3LYP PBEh, PBE0, B97-3 | TPSSh, M06, M06-2X | MN15 | |
| Screened Hybrid | HSE | MN12-SX | ||
| Range-Separated Hybrid (RSH) | CAM-B3LYP, ωB97X | M11, ωB97M | ||
| Double Hybrid | B2-PLYP, DSD-PBEP86 | |||
| Range-Separated Double Hybrid | B2-P3LYP, ωB97X-2 | ωB97M(2) |
Table 6: Selected DFT functionals
External Corrections
Sometimes it is just easiest to empirically correct shortcomings. Shortcomings in basis sets can be corrected with geometric counterpoise (GCP), short-range basis (SRB) corrections, or specifically tailored basis sets.
Composite Methods (3c)
Composite methods from the Grimme group combine specifically tailored basis sets and corrections to produce highly accurate results.
Table 7: 3c methods
In our experience, the following are the most useful (i.e. Pareto optimal):
- For quick geometry optimization: B97-3c
- For accurate geometry optimization: r2SCAN-3c
- For accurate thermochemistry: ωB97X-3c
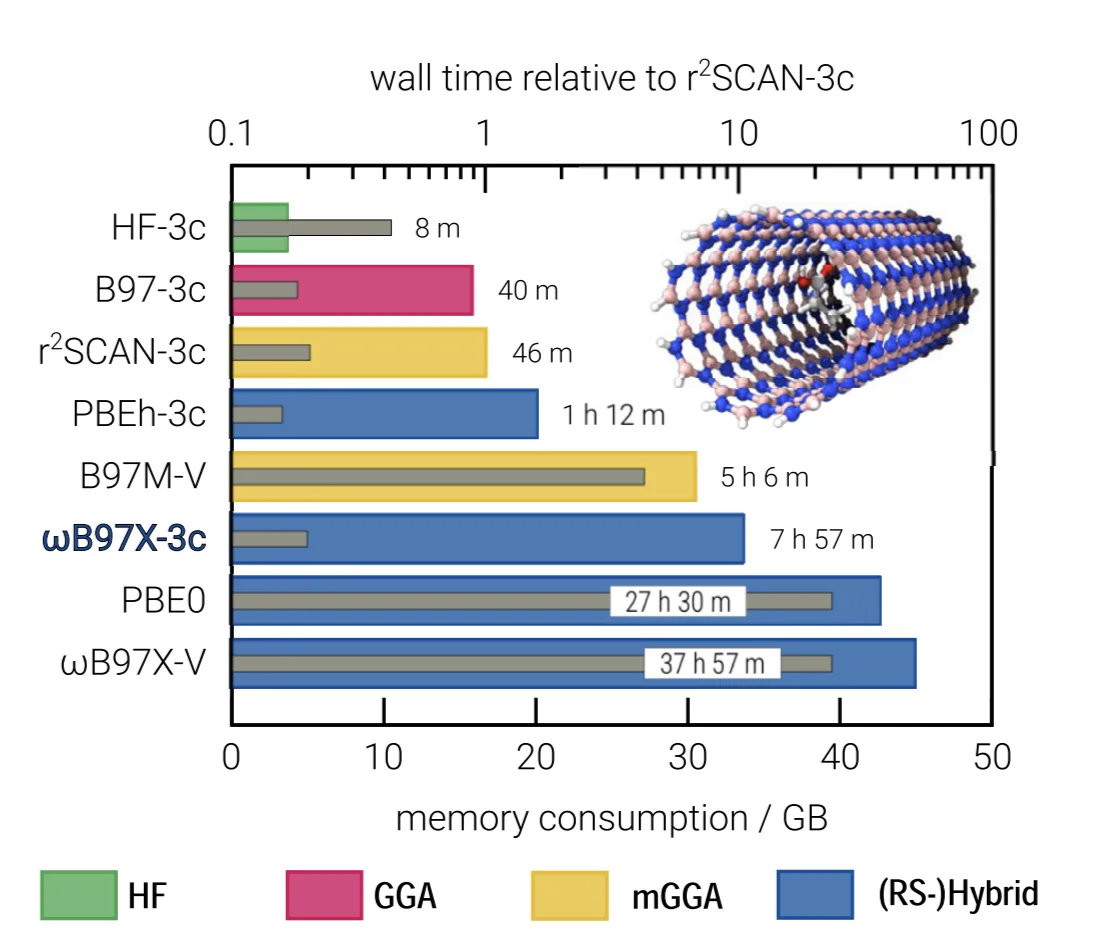
Figure 4: Wall time (top) and memory consumption (bottom) for calculating a single-point energy of a 381-atom boron-nitrogen nanotube containing an organic guest molecule (Müller, Hansen, and Grimme (2023)).
Conclusion
The web of density-functional theory can be confusing to most practitioners. There has been a proliferation of many functional forms and parameterizations, each with its benefits and drawbacks. The Rowan platform provides access to all of the above functional forms (except mNGAs): start running them today with free credits, and contact us if you have any questions.